GradientCobra Python Library

Introduction to MixCOBRA method

MixCOBRA is a consensual aggregation method that combines a given number of regressors based on their inputs and predicted features (A. Fischer and M. Mougeot, 2019). The method is summarized in the following figure.

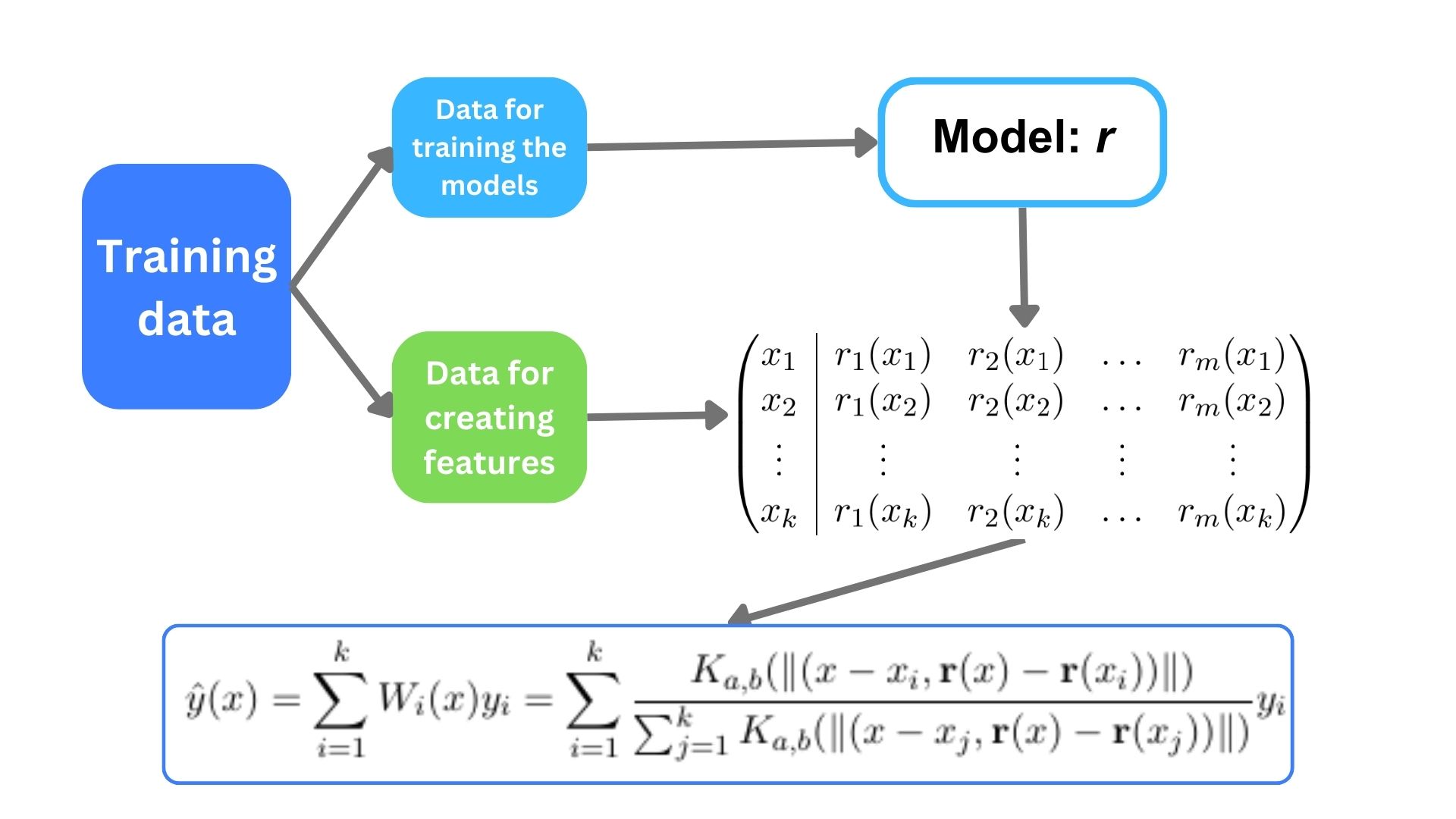
where

\({\bf r}(x)=(r_1(x),\dots, r_M(x))\) is the predicted features of observation \(x\).
\(K:\mathbb{R}_+\to\mathbb{R}_+\) is a regular kernel function that converts the “closeness” between predicted features of observation \(x_i\) and \(x\) into the associated weight for the aggregation. For any smoothing parameters \(a,b>0\), \(K_{a,b}(\|z,w\|)=K(\|(z/a,w/b)\|)\).

Constructing a consensual aggregation method is equivalent to estimating an appropriate smoothing parameters \((a,b)\) that minimizes the so-called \(\kappa\)-fold cross validation error:

\[\phi(h)=\frac{1}{\kappa}\sum_{j=1}^{\kappa}\sum_{(x_i,y_i)\in F_j}\ell(\hat{y}_{-F_j}(x_i),y_i)\]

where

\(\ell\) is any regression loss function. By default, \(\ell(y_1,y_2)=(y_1-y_2)^2\).
\((F_j)_{j=1,2,\dots,\kappa}\) are the \(\kappa\) folds of the second of the training data used for aggregation.
\(\hat{y}_{-F_j}(x)\) is the prediction of \(x\) by aggregating predicted features on all folds \((F_k)_{k}\) except for \(F_j\).

MixCOBRARegressor method

class MixCOBRARegressor(random_state = None, learning_rate = 0.01, speed = ‘constant’, estimator_list = None, estimator_params = None, opt_method = “grid”, opt_params = None, kernel = ‘radial’, kernel_exponent = 2.0, alpha_list = None, beta_list = None, bandwidth_list = None, max_iter =int(300), show_progress = True, loss_function = None, loss_weight = None, norm_constant_x = None, norm_constant_y = None):

Parameters

random_state: (default is None) for setting the random state of all the random generators in the class. This allows the method to produce the same result when the same random_state is used.
learning_rate: (default is 0.1) the learning rate in gradient descent algorithm for estimating the optimal bandwidth.
speed: (default is constant) for adjusting the speed of the learning rate. It is helpful when the cost function is flat around the optimal value, changing the learning speed might help the algorithm to converge faster. It should be an element of [‘constant’, ‘linear’, ‘log’, ‘sqrt_root’, ‘quad’, ‘exp’].
estimator_list: (default is None) the list of intial estimators. If it is None, the intial learners including ‘linear_regression’, ‘ridge’, ‘lasso’, ‘knn’, ‘random_forest’ and ‘svm’ are used with their default parameters. This argument should be a sublist of the following list: [‘linear_regression’, ‘knn’, ‘ridge’, ‘lasso’, ‘tree’, ‘random_forest’, ‘svm’, ‘sgd’, ‘bayesian_ridge’, ‘adaboost’, ‘gradient_boost’].
estimator_params: (default is None) a dictionary containing the parameters of the basic estimators given in the estimator_list argument. It must be a dictionary with:
- key: the name of the basic estimator defined in estimator_list,
- value: a dictionary with (key, value) = (parameter, value).
opt_method : (default is 'grid') an optimization algorithm for estimating the bandwidth parameter. It should be either 'grid' (grid search) or 'grad' (gradient descent for non-compactly supported kernels). By default, it is set to be 'grid' with default 'radial' kernel.
opt_params : (default is None) a dictionary of additional parameters for the optimization algorithm (both grid search and gradient descent). Its should contain some of the following keys:
- ‘epsilon’’: stopping criterion for gradient descent algorithm (default = \(10^{-6}\))
- ‘n_tries’: the number of tries for selecting initial position of gradient descent algorithm (default = \(5\)) ‘start’: the initial value of the bandwidth parameter (default = None)
- ‘n_cv’: number of cross-validation folds (default = int(10))
- ‘precision’: the precision to estimate the gradient for gradient descent algorithm (default = \(10^{-7}\)).
kernel: (default is 'radial') the kernel function used for the aggregation. It should be an element of the list [‘exponential’, ‘gaussian’, ‘radial’, ‘cauchy’, ‘reverse_cosh’,‘epanechnikov’,‘biweight’, ‘triweight’, ‘triangular’, ‘cobra’, ‘naive’]. Some options such as 'gaussian' and 'radial' lead to the same radial kernel function.
kernel_exponent: (default is 1.0) is an exponential \(\alpha\) of the exponential and radial kernel function i.e., \(K(x) = \exp(|x|^{2\alpha})\). By default, alpha = 1.0.
alpha_list and beta_list : (default are None) lists or arrays of alpha and beta (the first and second smoothing parameter) of MixCOBRA method. By default = None, the values of np.linspace(0.00001, 10, 50) are used.
bandwidth_list: a list of bandwidth parameters for 1D grid search algorithm where one smoothing parameter is used instead of two (default = np.linspace(0.00001, 10, 300)).
max_iter : (default is int(300)) maximum iteration of gradient descent algorithm (default = 300).
show_progress: (default is True) a boolean defining whether or not to show the progress of the optimization algorithm for both grid search and gradient descent.
loss_function : (default is None) a function or string defining the cost function to be optimized for estimating the optimal bandwidth or smoothing parameter. By defalut, the \(K\)-Fold cross-validation MSE is used. Otherwise, it must be either:
- a function of two argumetns (y_true, y_pred) or
- a string element of the list [‘mse’, ‘mae’, ‘mape’, ‘weighted_mse’]. If it is weighted_mse, one can define the weight for each training point using loss_weight argument below.
  - loss_weight : (default is None) a list of size \(n\) (the number of observations) defining the weight for each individual data point in the loss function. If it is None and the loss_function = weighted_mse, then a normalized weight \(W(i) = 1/\text{PDF}(i)\) is assigned to individual \(i\) of the training data.
norm_constant_x, norm_constant_y : (default is None) the normalization constants of inputs and output respectively. This allows to scale the range of the bandwidth parameters \((\alpha, \beta)\) to improve the optimization process.

Returns:

self : returns an instance of self containing the optimal estimated bandwidth and other results of the algorithm.

Methods:

fit: fitting the aggregation method on the design features (original data or predicted features).
split_data: split the data into \(D_k = \{(X_k,y_k)\}\) and \(D_{\ell} = \{(X_\ell,y_\ell)\}\) to construct the estimators and perform aggregation respectively.
build_basic_estimators: build basic estimators for the aggregation. It is also possible to set the values of (hyper) parameters for each estimators.
load_predictions: to make predictions using constructed basic estimators.
distances : construct distance matrix according to the kernel function used in the aggregation.
kappa_cross_validation_error: the objective function to be minimized for one parameter only.
kappa_cross_validation_error2: the objective function to be minimized for two parameters.
optimize_bandwidth: the optimization method to estimate the optimal bendwidth parameter.
predict: for building prediction on the new observations using any given bendwidth or the estimated one.
draw_learning_curve: for plotting the graphic of learning algorithm (error vs parameter).

Installation of the library from `pypi`

gradientcobra can be installed from pypi using pip:

pip install gradientcobra

Importing some packages

# Metric of error
from sklearn.metrics import mean_squared_error, mean_absolute_error, mean_absolute_percentage_error

# Plotting figures
import matplotlib.pyplot as plt
from matplotlib import cm

# Import class MixCOBRA from the mixcobra module of gradientcobra library
from gradientcobra.mixcobra import MixCOBRARegressor

import seaborn as sns
sns.set()

Simulated data

We simulate a regression data with \(1000\) observations and \(10\) inputs variables.

# For simulating dataset
from sklearn.datasets import make_regression

X1, y1 = make_regression(n_samples=1000, n_features=10, noise=1)

Now, let’s randoly split the simulated data into \(80\%-20\%\) training-testing data.

from sklearn.model_selection import train_test_split

X_train1, X_test1, y_train1, y_test1 = train_test_split(X1, y1, test_size=0.2)
print('shape: x_train = {} , x_train = {} , y_train = {} , y_test = {}'.format(
    X_train1.shape, 
    X_test1.shape, 
    y_train1.shape, 
    y_test1.shape))

shape: x_train = (800, 10) , x_train = (200, 10) , y_train = (800,) , y_test = (200,)

\(\bullet\) `MixCOBRARegressor` with default parameters

We create MixCOBRARegressor object called gc1, with the default parameters, then fit it to the training data.

Note that by default, we use grid search algorithm to estimate the optimal parameter of the method.

gc1 = MixCOBRARegressor()
gc1_fit = gc1.fit(X_train1, y_train1)

* 2D-grid search:   0%|          | 0/50 [00:00<?, ?it/s]* 2D-grid search:   2%|▏         | 1/50 [00:00<00:13,  3.52it/s]* 2D-grid search:   4%|▍         | 2/50 [00:00<00:15,  3.20it/s]* 2D-grid search:   6%|▌         | 3/50 [00:00<00:14,  3.26it/s]* 2D-grid search:   8%|▊         | 4/50 [00:01<00:13,  3.43it/s]* 2D-grid search:  10%|█         | 5/50 [00:01<00:13,  3.40it/s]* 2D-grid search:  12%|█▏        | 6/50 [00:01<00:12,  3.44it/s]* 2D-grid search:  14%|█▍        | 7/50 [00:02<00:12,  3.54it/s]* 2D-grid search:  16%|█▌        | 8/50 [00:02<00:11,  3.53it/s]* 2D-grid search:  18%|█▊        | 9/50 [00:02<00:12,  3.35it/s]* 2D-grid search:  20%|██        | 10/50 [00:02<00:11,  3.40it/s]* 2D-grid search:  22%|██▏       | 11/50 [00:03<00:11,  3.44it/s]* 2D-grid search:  24%|██▍       | 12/50 [00:03<00:11,  3.29it/s]* 2D-grid search:  26%|██▌       | 13/50 [00:03<00:11,  3.36it/s]* 2D-grid search:  28%|██▊       | 14/50 [00:04<00:10,  3.47it/s]* 2D-grid search:  30%|███       | 15/50 [00:04<00:10,  3.49it/s]* 2D-grid search:  32%|███▏      | 16/50 [00:04<00:09,  3.44it/s]* 2D-grid search:  34%|███▍      | 17/50 [00:05<00:10,  3.29it/s]* 2D-grid search:  36%|███▌      | 18/50 [00:05<00:09,  3.42it/s]* 2D-grid search:  38%|███▊      | 19/50 [00:05<00:08,  3.45it/s]* 2D-grid search:  40%|████      | 20/50 [00:05<00:08,  3.41it/s]* 2D-grid search:  42%|████▏     | 21/50 [00:06<00:08,  3.51it/s]* 2D-grid search:  44%|████▍     | 22/50 [00:06<00:08,  3.40it/s]* 2D-grid search:  46%|████▌     | 23/50 [00:06<00:08,  3.32it/s]* 2D-grid search:  48%|████▊     | 24/50 [00:07<00:07,  3.32it/s]* 2D-grid search:  50%|█████     | 25/50 [00:07<00:07,  3.33it/s]* 2D-grid search:  52%|█████▏    | 26/50 [00:07<00:06,  3.50it/s]* 2D-grid search:  54%|█████▍    | 27/50 [00:07<00:06,  3.51it/s]* 2D-grid search:  56%|█████▌    | 28/50 [00:08<00:06,  3.38it/s]* 2D-grid search:  58%|█████▊    | 29/50 [00:08<00:06,  3.44it/s]* 2D-grid search:  60%|██████    | 30/50 [00:08<00:06,  3.24it/s]* 2D-grid search:  62%|██████▏   | 31/50 [00:09<00:07,  2.62it/s]* 2D-grid search:  64%|██████▍   | 32/50 [00:09<00:06,  2.85it/s]* 2D-grid search:  66%|██████▌   | 33/50 [00:09<00:05,  2.98it/s]* 2D-grid search:  68%|██████▊   | 34/50 [00:10<00:05,  3.12it/s]* 2D-grid search:  70%|███████   | 35/50 [00:10<00:04,  3.13it/s]* 2D-grid search:  72%|███████▏  | 36/50 [00:10<00:04,  2.91it/s]* 2D-grid search:  74%|███████▍  | 37/50 [00:11<00:04,  2.66it/s]* 2D-grid search:  76%|███████▌  | 38/50 [00:11<00:04,  2.61it/s]* 2D-grid search:  78%|███████▊  | 39/50 [00:12<00:04,  2.54it/s]* 2D-grid search:  80%|████████  | 40/50 [00:12<00:04,  2.50it/s]* 2D-grid search:  82%|████████▏ | 41/50 [00:13<00:03,  2.38it/s]* 2D-grid search:  84%|████████▍ | 42/50 [00:13<00:03,  2.47it/s]* 2D-grid search:  86%|████████▌ | 43/50 [00:13<00:02,  2.42it/s]* 2D-grid search:  88%|████████▊ | 44/50 [00:14<00:02,  2.41it/s]* 2D-grid search:  90%|█████████ | 45/50 [00:14<00:02,  2.41it/s]* 2D-grid search:  92%|█████████▏| 46/50 [00:15<00:01,  2.27it/s]* 2D-grid search:  94%|█████████▍| 47/50 [00:15<00:01,  2.34it/s]* 2D-grid search:  96%|█████████▌| 48/50 [00:16<00:00,  2.47it/s]* 2D-grid search:  98%|█████████▊| 49/50 [00:16<00:00,  2.51it/s]* 2D-grid search: 100%|██████████| 50/50 [00:16<00:00,  2.51it/s]* 2D-grid search: 100%|██████████| 50/50 [00:16<00:00,  2.98it/s]

The estimated optimal bandwidth is given by gc1.optimization_outputs['opt_bandwidth'].

# MixCOBRA with default parameter
print("Estimated (alpha, beta) = ({}, {})".format(gc1_fit.optimization_outputs['opt_alpha'], gc1_fit.optimization_outputs['opt_beta']))

Estimated (alpha, beta) = (1e-05, 3.061231428571429)

We can look at the learning curve (surface) of the algorithm using draw_learning_curve() method.

gc1_fit.draw_learning_curve()

We evaluate the performance of the method on the testing data using MSE and MAPE.

from sklearn.metrics import mean_absolute_percentage_error
y_pred1 = gc1_fit.predict(X_test1)
print(mean_absolute_percentage_error(y_test1, y_pred1))
print(mean_squared_error(y_test1, y_pred1))

0.07021660186409182
71.6199568765435

Let’s look at qq-plot of the predictions and the actual response values using draw_learning_curve() method.

gc1_fit.draw_learning_curve(y_test=y_test1, fig_type='qq')

\(\bullet\) Use one bandwidth parameter instead of (\(\alpha, \beta\))

You can also try to implement MixCOBRARegressor using only one bandwidth parameter. To do so, just set one_parameter = True when fitting the method. We create another MixCOBRARegressor object with gradient descent optimization method, then fit it on the same data as in the previous case using only one bandwidth parameter as follow.

# MixCOBRA with one parameter
gc2 = MixCOBRARegressor(opt_method="grad")
gc2_fit = gc2.fit(X_train1, y_train1, one_parameter=True)

* 1D-GD:  iter: 1 / bw: 3.000 / grad: 111.051 / stop criter: inf :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 0 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]  * 1D-GD:  iter: 0 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 1 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 1 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 2 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 2 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 3 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 3 / bw: 2.990 / grad: 111.051 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 4 / bw: 2.990 / grad: -237.849 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 4 / bw: 2.990 / grad: -237.849 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 5 / bw: 3.011 / grad: -52.039 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s] * 1D-GD:  iter: 5 / bw: 3.011 / grad: -52.039 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 6 / bw: 3.016 / grad: -123.486 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 6 / bw: 3.016 / grad: -123.486 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 7 / bw: 3.026 / grad: 10.101 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]  * 1D-GD:  iter: 7 / bw: 3.026 / grad: 10.101 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 8 / bw: 3.025 / grad: -49.389 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 8 / bw: 3.025 / grad: -49.389 / stop at: 0.010 :   0%|          | 0/300 [00:00<?, ?it/s]* 1D-GD:  iter: 8 / bw: 3.025 / grad: -49.389 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 9 / bw: 3.028 / grad: 201.333 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 9 / bw: 3.028 / grad: 201.333 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 10 / bw: 3.015 / grad: -23.053 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 10 / bw: 3.015 / grad: -23.053 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 11 / bw: 3.017 / grad: -66.566 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 11 / bw: 3.017 / grad: -66.566 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 12 / bw: 3.020 / grad: 73.700 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s] * 1D-GD:  iter: 12 / bw: 3.020 / grad: 73.700 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 13 / bw: 3.016 / grad: -48.471 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 13 / bw: 3.016 / grad: -48.471 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 14 / bw: 3.019 / grad: 93.138 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s] * 1D-GD:  iter: 14 / bw: 3.019 / grad: 93.138 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 15 / bw: 3.015 / grad: 6.585 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s] * 1D-GD:  iter: 15 / bw: 3.015 / grad: 6.585 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 16 / bw: 3.014 / grad: -30.240 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 16 / bw: 3.014 / grad: -30.240 / stop at: 0.010 :   3%|▎         | 9/300 [00:00<00:03, 77.68it/s]* 1D-GD:  iter: 16 / bw: 3.014 / grad: -30.240 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 17 / bw: 3.015 / grad: -8.687 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s] * 1D-GD:  iter: 17 / bw: 3.015 / grad: -8.687 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 18 / bw: 3.016 / grad: 28.945 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 18 / bw: 3.016 / grad: 28.945 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 19 / bw: 3.015 / grad: -174.064 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 19 / bw: 3.015 / grad: -174.064 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 20 / bw: 3.020 / grad: -51.783 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s] * 1D-GD:  iter: 20 / bw: 3.020 / grad: -51.783 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 21 / bw: 3.022 / grad: -1.743 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s] * 1D-GD:  iter: 21 / bw: 3.022 / grad: -1.743 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 22 / bw: 3.022 / grad: 0.117 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s] * 1D-GD:  iter: 22 / bw: 3.022 / grad: 0.117 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 23 / bw: 3.022 / grad: -1.717 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 23 / bw: 3.022 / grad: -1.717 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 24 / bw: 3.022 / grad: -127.573 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 24 / bw: 3.022 / grad: -127.573 / stop at: 0.010 :   6%|▌         | 17/300 [00:00<00:03, 71.05it/s]* 1D-GD:  iter: 24 / bw: 3.022 / grad: -127.573 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 25 / bw: 3.025 / grad: 68.827 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]  * 1D-GD:  iter: 25 / bw: 3.025 / grad: 68.827 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 26 / bw: 3.023 / grad: 33.006 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 26 / bw: 3.023 / grad: 33.006 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 27 / bw: 3.022 / grad: -50.970 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 27 / bw: 3.022 / grad: -50.970 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 28 / bw: 3.023 / grad: -39.171 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 28 / bw: 3.023 / grad: -39.171 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 29 / bw: 3.024 / grad: -54.254 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 29 / bw: 3.024 / grad: -54.254 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 30 / bw: 3.025 / grad: 63.861 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s] * 1D-GD:  iter: 30 / bw: 3.025 / grad: 63.861 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 31 / bw: 3.024 / grad: -61.187 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 31 / bw: 3.024 / grad: -61.187 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 32 / bw: 3.025 / grad: 61.595 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s] * 1D-GD:  iter: 32 / bw: 3.025 / grad: 61.595 / stop at: 0.010 :   8%|▊         | 25/300 [00:00<00:03, 70.90it/s]* 1D-GD:  iter: 32 / bw: 3.025 / grad: 61.595 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 33 / bw: 3.024 / grad: -29.638 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 33 / bw: 3.024 / grad: -29.638 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 34 / bw: 3.024 / grad: -137.855 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 34 / bw: 3.024 / grad: -137.855 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 35 / bw: 3.026 / grad: 99.946 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]  * 1D-GD:  iter: 35 / bw: 3.026 / grad: 99.946 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 36 / bw: 3.025 / grad: 9.351 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s] * 1D-GD:  iter: 36 / bw: 3.025 / grad: 9.351 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 37 / bw: 3.025 / grad: -135.407 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 37 / bw: 3.025 / grad: -135.407 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 38 / bw: 3.026 / grad: -107.738 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 38 / bw: 3.026 / grad: -107.738 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 39 / bw: 3.027 / grad: 48.376 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]  * 1D-GD:  iter: 39 / bw: 3.027 / grad: 48.376 / stop at: 0.010 :  11%|█         | 33/300 [00:00<00:04, 66.06it/s]* 1D-GD:  iter: 39 / bw: 3.027 / grad: 48.376 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 40 / bw: 3.027 / grad: 48.010 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 40 / bw: 3.027 / grad: 48.010 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 41 / bw: 3.026 / grad: -71.067 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 41 / bw: 3.026 / grad: -71.067 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 42 / bw: 3.027 / grad: 86.224 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s] * 1D-GD:  iter: 42 / bw: 3.027 / grad: 86.224 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 43 / bw: 3.026 / grad: -128.832 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 43 / bw: 3.026 / grad: -128.832 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 44 / bw: 3.027 / grad: -57.462 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s] * 1D-GD:  iter: 44 / bw: 3.027 / grad: -57.462 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 45 / bw: 3.028 / grad: -8.152 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s] * 1D-GD:  iter: 45 / bw: 3.028 / grad: -8.152 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 46 / bw: 3.028 / grad: 60.506 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 46 / bw: 3.028 / grad: 60.506 / stop at: 0.010 :  13%|█▎        | 40/300 [00:00<00:04, 64.08it/s]* 1D-GD:  iter: 46 / bw: 3.028 / grad: 60.506 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 47 / bw: 3.027 / grad: -106.904 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 47 / bw: 3.027 / grad: -106.904 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 48 / bw: 3.028 / grad: 29.156 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]  * 1D-GD:  iter: 48 / bw: 3.028 / grad: 29.156 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 49 / bw: 3.028 / grad: -15.173 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 49 / bw: 3.028 / grad: -15.173 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 50 / bw: 3.028 / grad: -53.866 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 50 / bw: 3.028 / grad: -53.866 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 51 / bw: 3.028 / grad: 38.733 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s] * 1D-GD:  iter: 51 / bw: 3.028 / grad: 38.733 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 52 / bw: 3.028 / grad: 90.780 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 52 / bw: 3.028 / grad: 90.780 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 53 / bw: 3.028 / grad: -82.240 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 53 / bw: 3.028 / grad: -82.240 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 54 / bw: 3.028 / grad: -45.593 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 54 / bw: 3.028 / grad: -45.593 / stop at: 0.010 :  16%|█▌        | 47/300 [00:00<00:04, 62.67it/s]* 1D-GD:  iter: 54 / bw: 3.028 / grad: -45.593 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 55 / bw: 3.028 / grad: 1.954 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]  * 1D-GD:  iter: 55 / bw: 3.028 / grad: 1.954 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 56 / bw: 3.028 / grad: 12.730 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 56 / bw: 3.028 / grad: 12.730 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 57 / bw: 3.028 / grad: 38.825 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 57 / bw: 3.028 / grad: 38.825 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 58 / bw: 3.028 / grad: 79.392 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 58 / bw: 3.028 / grad: 79.392 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 59 / bw: 3.028 / grad: 198.099 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 59 / bw: 3.028 / grad: 198.099 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 60 / bw: 3.027 / grad: 18.983 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s] * 1D-GD:  iter: 60 / bw: 3.027 / grad: 18.983 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 61 / bw: 3.027 / grad: -75.729 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 61 / bw: 3.027 / grad: -75.729 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 62 / bw: 3.027 / grad: -25.767 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 62 / bw: 3.027 / grad: -25.767 / stop at: 0.010 :  18%|█▊        | 55/300 [00:00<00:03, 64.55it/s]* 1D-GD:  iter: 62 / bw: 3.027 / grad: -25.767 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 63 / bw: 3.027 / grad: 58.496 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s] * 1D-GD:  iter: 63 / bw: 3.027 / grad: 58.496 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 64 / bw: 3.027 / grad: 39.285 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 64 / bw: 3.027 / grad: 39.285 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 65 / bw: 3.027 / grad: 19.333 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 65 / bw: 3.027 / grad: 19.333 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 66 / bw: 3.027 / grad: 31.612 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 66 / bw: 3.027 / grad: 31.612 / stop at: 0.010 :  21%|██        | 63/300 [00:00<00:03, 65.92it/s]* 1D-GD:  iter: 67 / bw: 3.027 / grad: 8.968 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s] * 1D-GD:  iter: 67 / bw: 3.027 / grad: 8.968 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s]* 1D-GD:  iter: 68 / bw: 3.027 / grad: 88.363 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s]* 1D-GD:  iter: 68 / bw: 3.027 / grad: 88.363 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s]* 1D-GD:  iter: 69 / bw: 3.027 / grad: 77.688 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s]* 1D-GD:  iter: 69 / bw: 3.027 / grad: 77.688 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s]* 1D-GD:  iter: 70 / bw: 3.027 / grad: -65.194 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s]* 1D-GD:  iter: 70 / bw: 3.027 / grad: -65.194 / stop at: 0.010 :  21%|██        | 63/300 [00:01<00:03, 65.92it/s]* 1D-GD:  iter: 70 / bw: 3.027 / grad: -65.194 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 71 / bw: 3.027 / grad: -81.246 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 71 / bw: 3.027 / grad: -81.246 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 72 / bw: 3.027 / grad: 158.663 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 72 / bw: 3.027 / grad: 158.663 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 73 / bw: 3.027 / grad: -44.777 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 73 / bw: 3.027 / grad: -44.777 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 74 / bw: 3.027 / grad: -35.055 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 74 / bw: 3.027 / grad: -35.055 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 75 / bw: 3.027 / grad: 86.048 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s] * 1D-GD:  iter: 75 / bw: 3.027 / grad: 86.048 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 76 / bw: 3.027 / grad: -48.836 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 76 / bw: 3.027 / grad: -48.836 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 77 / bw: 3.027 / grad: -28.414 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 77 / bw: 3.027 / grad: -28.414 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 78 / bw: 3.027 / grad: -95.005 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 78 / bw: 3.027 / grad: -95.005 / stop at: 0.010 :  24%|██▎       | 71/300 [00:01<00:03, 69.80it/s]* 1D-GD:  iter: 78 / bw: 3.027 / grad: -95.005 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 79 / bw: 3.027 / grad: -31.823 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 79 / bw: 3.027 / grad: -31.823 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 80 / bw: 3.027 / grad: -100.378 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 80 / bw: 3.027 / grad: -100.378 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 81 / bw: 3.027 / grad: 33.369 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]  * 1D-GD:  iter: 81 / bw: 3.027 / grad: 33.369 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 82 / bw: 3.027 / grad: 93.539 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 82 / bw: 3.027 / grad: 93.539 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 83 / bw: 3.027 / grad: 100.801 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 83 / bw: 3.027 / grad: 100.801 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 84 / bw: 3.027 / grad: -46.738 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 84 / bw: 3.027 / grad: -46.738 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 85 / bw: 3.027 / grad: 89.577 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s] * 1D-GD:  iter: 85 / bw: 3.027 / grad: 89.577 / stop at: 0.010 :  26%|██▋       | 79/300 [00:01<00:03, 66.30it/s]* 1D-GD:  iter: 85 / bw: 3.027 / grad: 89.577 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 86 / bw: 3.027 / grad: 90.966 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 86 / bw: 3.027 / grad: 90.966 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 87 / bw: 3.027 / grad: -19.395 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 87 / bw: 3.027 / grad: -19.395 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 88 / bw: 3.027 / grad: -3.818 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s] * 1D-GD:  iter: 88 / bw: 3.027 / grad: -3.818 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 89 / bw: 3.027 / grad: -120.126 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 89 / bw: 3.027 / grad: -120.126 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 90 / bw: 3.027 / grad: -2.140 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]  * 1D-GD:  iter: 90 / bw: 3.027 / grad: -2.140 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 91 / bw: 3.027 / grad: -21.283 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 91 / bw: 3.027 / grad: -21.283 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 92 / bw: 3.027 / grad: -118.693 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 92 / bw: 3.027 / grad: -118.693 / stop at: 0.010 :  29%|██▊       | 86/300 [00:01<00:03, 64.52it/s]* 1D-GD:  iter: 92 / bw: 3.027 / grad: -118.693 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 93 / bw: 3.027 / grad: 80.252 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]  * 1D-GD:  iter: 93 / bw: 3.027 / grad: 80.252 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 94 / bw: 3.027 / grad: -63.112 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 94 / bw: 3.027 / grad: -63.112 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 95 / bw: 3.027 / grad: 6.361 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]  * 1D-GD:  iter: 95 / bw: 3.027 / grad: 6.361 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 96 / bw: 3.027 / grad: 1.653 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 96 / bw: 3.027 / grad: 1.653 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 97 / bw: 3.027 / grad: -40.128 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 97 / bw: 3.027 / grad: -40.128 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 98 / bw: 3.027 / grad: 15.747 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s] * 1D-GD:  iter: 98 / bw: 3.027 / grad: 15.747 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 99 / bw: 3.027 / grad: -0.417 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 99 / bw: 3.027 / grad: -0.417 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 100 / bw: 3.027 / grad: 33.531 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 100 / bw: 3.027 / grad: 33.531 / stop at: 0.010 :  31%|███       | 93/300 [00:01<00:03, 62.90it/s]* 1D-GD:  iter: 100 / bw: 3.027 / grad: 33.531 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 101 / bw: 3.027 / grad: 94.459 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 101 / bw: 3.027 / grad: 94.459 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 102 / bw: 3.027 / grad: 24.447 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 102 / bw: 3.027 / grad: 24.447 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 103 / bw: 3.027 / grad: 104.649 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 103 / bw: 3.027 / grad: 104.649 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 104 / bw: 3.027 / grad: -0.141 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s] * 1D-GD:  iter: 104 / bw: 3.027 / grad: -0.141 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 105 / bw: 3.027 / grad: 71.605 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 105 / bw: 3.027 / grad: 71.605 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 106 / bw: 3.027 / grad: 40.858 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 106 / bw: 3.027 / grad: 40.858 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 107 / bw: 3.027 / grad: 25.934 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 107 / bw: 3.027 / grad: 25.934 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 108 / bw: 3.027 / grad: -49.070 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 108 / bw: 3.027 / grad: -49.070 / stop at: 0.010 :  34%|███▎      | 101/300 [00:01<00:03, 64.76it/s]* 1D-GD:  iter: 108 / bw: 3.027 / grad: -49.070 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 109 / bw: 3.027 / grad: -59.938 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 109 / bw: 3.027 / grad: -59.938 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 110 / bw: 3.027 / grad: 140.915 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 110 / bw: 3.027 / grad: 140.915 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 111 / bw: 3.027 / grad: 19.485 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s] * 1D-GD:  iter: 111 / bw: 3.027 / grad: 19.485 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 112 / bw: 3.027 / grad: -6.125 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 112 / bw: 3.027 / grad: -6.125 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 113 / bw: 3.027 / grad: -114.516 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 113 / bw: 3.027 / grad: -114.516 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 114 / bw: 3.027 / grad: -13.612 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s] * 1D-GD:  iter: 114 / bw: 3.027 / grad: -13.612 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 115 / bw: 3.027 / grad: 203.130 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 115 / bw: 3.027 / grad: 203.130 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 116 / bw: 3.027 / grad: 58.827 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s] * 1D-GD:  iter: 116 / bw: 3.027 / grad: 58.827 / stop at: 0.010 :  36%|███▋      | 109/300 [00:01<00:02, 65.99it/s]* 1D-GD:  iter: 116 / bw: 3.027 / grad: 58.827 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 117 / bw: 3.027 / grad: 51.354 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 117 / bw: 3.027 / grad: 51.354 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 118 / bw: 3.027 / grad: 58.664 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 118 / bw: 3.027 / grad: 58.664 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 119 / bw: 3.027 / grad: -60.615 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 119 / bw: 3.027 / grad: -60.615 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 120 / bw: 3.027 / grad: -81.384 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 120 / bw: 3.027 / grad: -81.384 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 121 / bw: 3.027 / grad: -24.232 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 121 / bw: 3.027 / grad: -24.232 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 122 / bw: 3.027 / grad: 53.242 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s] * 1D-GD:  iter: 122 / bw: 3.027 / grad: 53.242 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 123 / bw: 3.027 / grad: 155.295 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 123 / bw: 3.027 / grad: 155.295 / stop at: 0.010 :  39%|███▉      | 117/300 [00:01<00:02, 66.76it/s]* 1D-GD:  iter: 123 / bw: 3.027 / grad: 155.295 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 124 / bw: 3.027 / grad: -96.878 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 124 / bw: 3.027 / grad: -96.878 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 125 / bw: 3.027 / grad: -64.482 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 125 / bw: 3.027 / grad: -64.482 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 126 / bw: 3.027 / grad: -19.389 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 126 / bw: 3.027 / grad: -19.389 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 127 / bw: 3.027 / grad: 17.976 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s] * 1D-GD:  iter: 127 / bw: 3.027 / grad: 17.976 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 128 / bw: 3.027 / grad: 2.367 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s] * 1D-GD:  iter: 128 / bw: 3.027 / grad: 2.367 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 129 / bw: 3.027 / grad: -122.847 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 129 / bw: 3.027 / grad: -122.847 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 130 / bw: 3.027 / grad: -41.479 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s] * 1D-GD:  iter: 130 / bw: 3.027 / grad: -41.479 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 131 / bw: 3.027 / grad: 77.812 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s] * 1D-GD:  iter: 131 / bw: 3.027 / grad: 77.812 / stop at: 0.010 :  41%|████▏     | 124/300 [00:01<00:02, 67.50it/s]* 1D-GD:  iter: 131 / bw: 3.027 / grad: 77.812 / stop at: 0.010 :  44%|████▍     | 132/300 [00:01<00:02, 67.92it/s]* 1D-GD:  iter: 132 / bw: 3.027 / grad: -59.012 / stop at: 0.010 :  44%|████▍     | 132/300 [00:01<00:02, 67.92it/s]* 1D-GD:  iter: 132 / bw: 3.027 / grad: -59.012 / stop at: 0.010 :  44%|████▍     | 132/300 [00:01<00:02, 67.92it/s]* 1D-GD:  iter: 133 / bw: 3.027 / grad: -3.993 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s] * 1D-GD:  iter: 133 / bw: 3.027 / grad: -3.993 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 134 / bw: 3.027 / grad: 91.908 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 134 / bw: 3.027 / grad: 91.908 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 135 / bw: 3.027 / grad: 17.024 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 135 / bw: 3.027 / grad: 17.024 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 136 / bw: 3.027 / grad: 75.223 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 136 / bw: 3.027 / grad: 75.223 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 137 / bw: 3.027 / grad: 19.327 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 137 / bw: 3.027 / grad: 19.327 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 138 / bw: 3.027 / grad: 64.268 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 138 / bw: 3.027 / grad: 64.268 / stop at: 0.010 :  44%|████▍     | 132/300 [00:02<00:02, 67.92it/s]* 1D-GD:  iter: 138 / bw: 3.027 / grad: 64.268 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 139 / bw: 3.027 / grad: -38.120 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 139 / bw: 3.027 / grad: -38.120 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 140 / bw: 3.027 / grad: -94.686 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 140 / bw: 3.027 / grad: -94.686 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 141 / bw: 3.027 / grad: 38.611 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s] * 1D-GD:  iter: 141 / bw: 3.027 / grad: 38.611 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 142 / bw: 3.027 / grad: 57.802 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 142 / bw: 3.027 / grad: 57.802 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 143 / bw: 3.027 / grad: -83.997 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 143 / bw: 3.027 / grad: -83.997 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 144 / bw: 3.027 / grad: -28.202 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 144 / bw: 3.027 / grad: -28.202 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 145 / bw: 3.027 / grad: -186.991 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 145 / bw: 3.027 / grad: -186.991 / stop at: 0.010 :  46%|████▋     | 139/300 [00:02<00:02, 68.46it/s]* 1D-GD:  iter: 145 / bw: 3.027 / grad: -186.991 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 146 / bw: 3.027 / grad: -79.922 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s] * 1D-GD:  iter: 146 / bw: 3.027 / grad: -79.922 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 147 / bw: 3.027 / grad: -20.429 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 147 / bw: 3.027 / grad: -20.429 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 148 / bw: 3.027 / grad: 25.060 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s] * 1D-GD:  iter: 148 / bw: 3.027 / grad: 25.060 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 149 / bw: 3.027 / grad: 98.279 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 149 / bw: 3.027 / grad: 98.279 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 150 / bw: 3.027 / grad: 109.752 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 150 / bw: 3.027 / grad: 109.752 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 151 / bw: 3.027 / grad: 18.740 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s] * 1D-GD:  iter: 151 / bw: 3.027 / grad: 18.740 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 152 / bw: 3.027 / grad: -101.046 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 152 / bw: 3.027 / grad: -101.046 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 153 / bw: 3.027 / grad: -48.672 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s] * 1D-GD:  iter: 153 / bw: 3.027 / grad: -48.672 / stop at: 0.010 :  49%|████▊     | 146/300 [00:02<00:02, 65.92it/s]* 1D-GD:  iter: 153 / bw: 3.027 / grad: -48.672 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 154 / bw: 3.027 / grad: 1.588 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]  * 1D-GD:  iter: 154 / bw: 3.027 / grad: 1.588 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 155 / bw: 3.027 / grad: -59.637 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 155 / bw: 3.027 / grad: -59.637 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 156 / bw: 3.027 / grad: 274.104 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 156 / bw: 3.027 / grad: 274.104 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 157 / bw: 3.027 / grad: 97.357 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s] * 1D-GD:  iter: 157 / bw: 3.027 / grad: 97.357 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 158 / bw: 3.027 / grad: -53.460 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 158 / bw: 3.027 / grad: -53.460 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 159 / bw: 3.027 / grad: -29.993 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 159 / bw: 3.027 / grad: -29.993 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 160 / bw: 3.027 / grad: 8.608 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]  * 1D-GD:  iter: 160 / bw: 3.027 / grad: 8.608 / stop at: 0.010 :  51%|█████▏    | 154/300 [00:02<00:02, 66.72it/s]* 1D-GD:  iter: 160 / bw: 3.027 / grad: 8.608 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 161 / bw: 3.027 / grad: -3.401 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 161 / bw: 3.027 / grad: -3.401 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 162 / bw: 3.027 / grad: 27.613 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 162 / bw: 3.027 / grad: 27.613 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 163 / bw: 3.027 / grad: 27.963 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 163 / bw: 3.027 / grad: 27.963 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 164 / bw: 3.027 / grad: -16.498 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 164 / bw: 3.027 / grad: -16.498 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 165 / bw: 3.027 / grad: -37.191 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 165 / bw: 3.027 / grad: -37.191 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 166 / bw: 3.027 / grad: 11.869 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s] * 1D-GD:  iter: 166 / bw: 3.027 / grad: 11.869 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 167 / bw: 3.027 / grad: -22.589 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 167 / bw: 3.027 / grad: -22.589 / stop at: 0.010 :  54%|█████▎    | 161/300 [00:02<00:02, 64.57it/s]* 1D-GD:  iter: 167 / bw: 3.027 / grad: -22.589 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 168 / bw: 3.027 / grad: 43.397 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s] * 1D-GD:  iter: 168 / bw: 3.027 / grad: 43.397 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 169 / bw: 3.027 / grad: 18.068 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 169 / bw: 3.027 / grad: 18.068 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 170 / bw: 3.027 / grad: 45.381 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 170 / bw: 3.027 / grad: 45.381 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 171 / bw: 3.027 / grad: -94.629 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 171 / bw: 3.027 / grad: -94.629 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 172 / bw: 3.027 / grad: -44.635 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 172 / bw: 3.027 / grad: -44.635 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 173 / bw: 3.027 / grad: 102.789 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 173 / bw: 3.027 / grad: 102.789 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 174 / bw: 3.027 / grad: 77.072 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s] * 1D-GD:  iter: 174 / bw: 3.027 / grad: 77.072 / stop at: 0.010 :  56%|█████▌    | 168/300 [00:02<00:02, 63.26it/s]* 1D-GD:  iter: 174 / bw: 3.027 / grad: 77.072 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 175 / bw: 3.027 / grad: -3.697 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 175 / bw: 3.027 / grad: -3.697 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 176 / bw: 3.027 / grad: -73.529 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 176 / bw: 3.027 / grad: -73.529 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 177 / bw: 3.027 / grad: -17.517 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 177 / bw: 3.027 / grad: -17.517 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 178 / bw: 3.027 / grad: -43.866 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 178 / bw: 3.027 / grad: -43.866 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 179 / bw: 3.027 / grad: -81.758 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 179 / bw: 3.027 / grad: -81.758 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 180 / bw: 3.027 / grad: -50.266 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 180 / bw: 3.027 / grad: -50.266 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 181 / bw: 3.027 / grad: 44.256 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s] * 1D-GD:  iter: 181 / bw: 3.027 / grad: 44.256 / stop at: 0.010 :  58%|█████▊    | 175/300 [00:02<00:02, 59.40it/s]* 1D-GD:  iter: 181 / bw: 3.027 / grad: 44.256 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 182 / bw: 3.027 / grad: -126.024 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 182 / bw: 3.027 / grad: -126.024 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 183 / bw: 3.027 / grad: -54.902 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s] * 1D-GD:  iter: 183 / bw: 3.027 / grad: -54.902 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 184 / bw: 3.027 / grad: 18.781 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s] * 1D-GD:  iter: 184 / bw: 3.027 / grad: 18.781 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 185 / bw: 3.027 / grad: -158.496 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 185 / bw: 3.027 / grad: -158.496 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 186 / bw: 3.027 / grad: -99.200 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s] * 1D-GD:  iter: 186 / bw: 3.027 / grad: -99.200 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 187 / bw: 3.027 / grad: -51.979 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 187 / bw: 3.027 / grad: -51.979 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 188 / bw: 3.027 / grad: -83.332 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 188 / bw: 3.027 / grad: -83.332 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 189 / bw: 3.027 / grad: -62.812 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 189 / bw: 3.027 / grad: -62.812 / stop at: 0.010 :  61%|██████    | 182/300 [00:02<00:01, 59.88it/s]* 1D-GD:  iter: 189 / bw: 3.027 / grad: -62.812 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 190 / bw: 3.027 / grad: -2.696 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s] * 1D-GD:  iter: 190 / bw: 3.027 / grad: -2.696 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 191 / bw: 3.027 / grad: -38.687 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 191 / bw: 3.027 / grad: -38.687 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 192 / bw: 3.027 / grad: 23.237 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s] * 1D-GD:  iter: 192 / bw: 3.027 / grad: 23.237 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 193 / bw: 3.027 / grad: 25.166 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 193 / bw: 3.027 / grad: 25.166 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 194 / bw: 3.027 / grad: 20.021 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 194 / bw: 3.027 / grad: 20.021 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:02<00:01, 62.45it/s]* 1D-GD:  iter: 195 / bw: 3.027 / grad: 62.431 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]* 1D-GD:  iter: 195 / bw: 3.027 / grad: 62.431 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]* 1D-GD:  iter: 196 / bw: 3.027 / grad: 36.537 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]* 1D-GD:  iter: 196 / bw: 3.027 / grad: 36.537 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]* 1D-GD:  iter: 197 / bw: 3.027 / grad: -132.829 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]* 1D-GD:  iter: 197 / bw: 3.027 / grad: -132.829 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]* 1D-GD:  iter: 198 / bw: 3.027 / grad: -5.728 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]  * 1D-GD:  iter: 198 / bw: 3.027 / grad: -5.728 / stop at: 0.010 :  63%|██████▎   | 190/300 [00:03<00:01, 62.45it/s]* 1D-GD:  iter: 198 / bw: 3.027 / grad: -5.728 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 199 / bw: 3.027 / grad: 38.414 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 199 / bw: 3.027 / grad: 38.414 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 200 / bw: 3.027 / grad: 70.078 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 200 / bw: 3.027 / grad: 70.078 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 201 / bw: 3.027 / grad: 87.630 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 201 / bw: 3.027 / grad: 87.630 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 202 / bw: 3.027 / grad: -9.090 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 202 / bw: 3.027 / grad: -9.090 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 203 / bw: 3.027 / grad: -15.965 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 203 / bw: 3.027 / grad: -15.965 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 204 / bw: 3.027 / grad: 28.466 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s] * 1D-GD:  iter: 204 / bw: 3.027 / grad: 28.466 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 205 / bw: 3.027 / grad: 106.393 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 205 / bw: 3.027 / grad: 106.393 / stop at: 0.010 :  66%|██████▋   | 199/300 [00:03<00:01, 66.76it/s]* 1D-GD:  iter: 205 / bw: 3.027 / grad: 106.393 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 206 / bw: 3.027 / grad: -23.772 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 206 / bw: 3.027 / grad: -23.772 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 207 / bw: 3.027 / grad: -36.878 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 207 / bw: 3.027 / grad: -36.878 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 208 / bw: 3.027 / grad: 53.424 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s] * 1D-GD:  iter: 208 / bw: 3.027 / grad: 53.424 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 209 / bw: 3.027 / grad: -20.119 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 209 / bw: 3.027 / grad: -20.119 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 210 / bw: 3.027 / grad: -123.498 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 210 / bw: 3.027 / grad: -123.498 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 211 / bw: 3.027 / grad: 74.458 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]  * 1D-GD:  iter: 211 / bw: 3.027 / grad: 74.458 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 212 / bw: 3.027 / grad: -99.737 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 212 / bw: 3.027 / grad: -99.737 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 213 / bw: 3.027 / grad: -22.554 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 213 / bw: 3.027 / grad: -22.554 / stop at: 0.010 :  69%|██████▊   | 206/300 [00:03<00:01, 67.62it/s]* 1D-GD:  iter: 213 / bw: 3.027 / grad: -22.554 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 214 / bw: 3.027 / grad: 33.920 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s] * 1D-GD:  iter: 214 / bw: 3.027 / grad: 33.920 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 215 / bw: 3.027 / grad: 27.279 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 215 / bw: 3.027 / grad: 27.279 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 216 / bw: 3.027 / grad: 155.706 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 216 / bw: 3.027 / grad: 155.706 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 217 / bw: 3.027 / grad: -78.654 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 217 / bw: 3.027 / grad: -78.654 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 218 / bw: 3.027 / grad: 13.115 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s] * 1D-GD:  iter: 218 / bw: 3.027 / grad: 13.115 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 219 / bw: 3.027 / grad: 87.932 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 219 / bw: 3.027 / grad: 87.932 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 220 / bw: 3.027 / grad: -31.200 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 220 / bw: 3.027 / grad: -31.200 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 221 / bw: 3.027 / grad: -124.627 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 221 / bw: 3.027 / grad: -124.627 / stop at: 0.010 :  71%|███████▏  | 214/300 [00:03<00:01, 70.34it/s]* 1D-GD:  iter: 221 / bw: 3.027 / grad: -124.627 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 222 / bw: 3.027 / grad: -49.147 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s] * 1D-GD:  iter: 222 / bw: 3.027 / grad: -49.147 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 223 / bw: 3.027 / grad: -14.960 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 223 / bw: 3.027 / grad: -14.960 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 224 / bw: 3.027 / grad: 92.441 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s] * 1D-GD:  iter: 224 / bw: 3.027 / grad: 92.441 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 225 / bw: 3.027 / grad: 61.576 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 225 / bw: 3.027 / grad: 61.576 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 226 / bw: 3.027 / grad: 51.026 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 226 / bw: 3.027 / grad: 51.026 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 227 / bw: 3.027 / grad: -9.188 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 227 / bw: 3.027 / grad: -9.188 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 228 / bw: 3.027 / grad: -145.540 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 228 / bw: 3.027 / grad: -145.540 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 229 / bw: 3.027 / grad: -13.273 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s] * 1D-GD:  iter: 229 / bw: 3.027 / grad: -13.273 / stop at: 0.010 :  74%|███████▍  | 222/300 [00:03<00:01, 70.61it/s]* 1D-GD:  iter: 229 / bw: 3.027 / grad: -13.273 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 230 / bw: 3.027 / grad: -57.862 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 230 / bw: 3.027 / grad: -57.862 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 231 / bw: 3.027 / grad: -10.270 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 231 / bw: 3.027 / grad: -10.270 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 232 / bw: 3.027 / grad: 122.447 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 232 / bw: 3.027 / grad: 122.447 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 233 / bw: 3.027 / grad: 147.887 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 233 / bw: 3.027 / grad: 147.887 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 234 / bw: 3.027 / grad: -164.313 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 234 / bw: 3.027 / grad: -164.313 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 235 / bw: 3.027 / grad: 47.498 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]  * 1D-GD:  iter: 235 / bw: 3.027 / grad: 47.498 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 236 / bw: 3.027 / grad: -20.935 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 236 / bw: 3.027 / grad: -20.935 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 237 / bw: 3.027 / grad: 5.872 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]  * 1D-GD:  iter: 237 / bw: 3.027 / grad: 5.872 / stop at: 0.010 :  77%|███████▋  | 230/300 [00:03<00:01, 69.93it/s]* 1D-GD:  iter: 237 / bw: 3.027 / grad: 5.872 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 238 / bw: 3.027 / grad: 92.373 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 238 / bw: 3.027 / grad: 92.373 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 239 / bw: 3.027 / grad: -30.402 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 239 / bw: 3.027 / grad: -30.402 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 240 / bw: 3.027 / grad: -50.873 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 240 / bw: 3.027 / grad: -50.873 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 241 / bw: 3.027 / grad: -102.900 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 241 / bw: 3.027 / grad: -102.900 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 242 / bw: 3.027 / grad: -30.561 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s] * 1D-GD:  iter: 242 / bw: 3.027 / grad: -30.561 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 243 / bw: 3.027 / grad: -22.191 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 243 / bw: 3.027 / grad: -22.191 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 244 / bw: 3.027 / grad: -197.346 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 244 / bw: 3.027 / grad: -197.346 / stop at: 0.010 :  79%|███████▉  | 238/300 [00:03<00:00, 69.43it/s]* 1D-GD:  iter: 244 / bw: 3.027 / grad: -197.346 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 245 / bw: 3.027 / grad: 21.441 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]  * 1D-GD:  iter: 245 / bw: 3.027 / grad: 21.441 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 246 / bw: 3.027 / grad: 16.844 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 246 / bw: 3.027 / grad: 16.844 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 247 / bw: 3.027 / grad: 98.828 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 247 / bw: 3.027 / grad: 98.828 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 248 / bw: 3.027 / grad: 0.924 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s] * 1D-GD:  iter: 248 / bw: 3.027 / grad: 0.924 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 249 / bw: 3.027 / grad: 73.824 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 249 / bw: 3.027 / grad: 73.824 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 250 / bw: 3.027 / grad: -103.446 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 250 / bw: 3.027 / grad: -103.446 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 251 / bw: 3.027 / grad: -63.884 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s] * 1D-GD:  iter: 251 / bw: 3.027 / grad: -63.884 / stop at: 0.010 :  82%|████████▏ | 245/300 [00:03<00:00, 69.58it/s]* 1D-GD:  iter: 251 / bw: 3.027 / grad: -63.884 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 252 / bw: 3.027 / grad: 2.071 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]  * 1D-GD:  iter: 252 / bw: 3.027 / grad: 2.071 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 253 / bw: 3.027 / grad: 29.717 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 253 / bw: 3.027 / grad: 29.717 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 254 / bw: 3.027 / grad: -39.879 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 254 / bw: 3.027 / grad: -39.879 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 255 / bw: 3.027 / grad: 4.722 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]  * 1D-GD:  iter: 255 / bw: 3.027 / grad: 4.722 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 256 / bw: 3.027 / grad: 32.502 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 256 / bw: 3.027 / grad: 32.502 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 257 / bw: 3.027 / grad: -11.956 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 257 / bw: 3.027 / grad: -11.956 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 258 / bw: 3.027 / grad: 35.054 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s] * 1D-GD:  iter: 258 / bw: 3.027 / grad: 35.054 / stop at: 0.010 :  84%|████████▍ | 252/300 [00:03<00:00, 69.69it/s]* 1D-GD:  iter: 258 / bw: 3.027 / grad: 35.054 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 259 / bw: 3.027 / grad: 41.179 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 259 / bw: 3.027 / grad: 41.179 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 260 / bw: 3.027 / grad: -101.892 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 260 / bw: 3.027 / grad: -101.892 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 261 / bw: 3.027 / grad: 14.487 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]  * 1D-GD:  iter: 261 / bw: 3.027 / grad: 14.487 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 262 / bw: 3.027 / grad: 74.069 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 262 / bw: 3.027 / grad: 74.069 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 263 / bw: 3.027 / grad: 145.291 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 263 / bw: 3.027 / grad: 145.291 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 264 / bw: 3.027 / grad: 59.022 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s] * 1D-GD:  iter: 264 / bw: 3.027 / grad: 59.022 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 265 / bw: 3.027 / grad: 80.230 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 265 / bw: 3.027 / grad: 80.230 / stop at: 0.010 :  86%|████████▋ | 259/300 [00:03<00:00, 69.67it/s]* 1D-GD:  iter: 265 / bw: 3.027 / grad: 80.230 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:03<00:00, 69.76it/s]* 1D-GD:  iter: 266 / bw: 3.027 / grad: -88.440 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:03<00:00, 69.76it/s]* 1D-GD:  iter: 266 / bw: 3.027 / grad: -88.440 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:03<00:00, 69.76it/s]* 1D-GD:  iter: 267 / bw: 3.027 / grad: 45.937 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s] * 1D-GD:  iter: 267 / bw: 3.027 / grad: 45.937 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 268 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s] * 1D-GD:  iter: 268 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 269 / bw: 3.027 / grad: -8.588 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 269 / bw: 3.027 / grad: -8.588 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 270 / bw: 3.027 / grad: 4.339 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s] * 1D-GD:  iter: 270 / bw: 3.027 / grad: 4.339 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 271 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 271 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 272 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 272 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  89%|████████▊ | 266/300 [00:04<00:00, 69.76it/s]* 1D-GD:  iter: 272 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 273 / bw: 3.027 / grad: -8.588 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 273 / bw: 3.027 / grad: -8.588 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 274 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s] * 1D-GD:  iter: 274 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 275 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 275 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 276 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 276 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 277 / bw: 3.027 / grad: -11.568 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 277 / bw: 3.027 / grad: -11.568 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 278 / bw: 3.027 / grad: 4.339 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]  * 1D-GD:  iter: 278 / bw: 3.027 / grad: 4.339 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 279 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 279 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 280 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 280 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  91%|█████████ | 273/300 [00:04<00:00, 66.71it/s]* 1D-GD:  iter: 280 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 281 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 281 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 282 / bw: 3.027 / grad: -11.568 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 282 / bw: 3.027 / grad: -11.568 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 283 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]  * 1D-GD:  iter: 283 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 284 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 284 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 285 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 285 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 286 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 286 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 287 / bw: 3.027 / grad: -13.010 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 287 / bw: 3.027 / grad: -13.010 / stop at: 0.010 :  94%|█████████▎| 281/300 [00:04<00:00, 67.42it/s]* 1D-GD:  iter: 287 / bw: 3.027 / grad: -13.010 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 288 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]  * 1D-GD:  iter: 288 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 289 / bw: 3.027 / grad: 2.829 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 289 / bw: 3.027 / grad: 2.829 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 290 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 290 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 291 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 291 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 292 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 292 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 293 / bw: 3.027 / grad: -13.010 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 293 / bw: 3.027 / grad: -13.010 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 294 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]  * 1D-GD:  iter: 294 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  96%|█████████▌| 288/300 [00:04<00:00, 68.08it/s]* 1D-GD:  iter: 294 / bw: 3.027 / grad: 2.767 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 295 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 295 / bw: 3.027 / grad: 2.999 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 296 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 296 / bw: 3.027 / grad: 3.261 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 297 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 297 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 298 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 298 / bw: 3.027 / grad: 2.944 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 299 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 299 / bw: 3.027 / grad: 2.967 / stop at: 0.010 :  98%|█████████▊| 295/300 [00:04<00:00, 65.37it/s]* 1D-GD:  iter: 299 / bw: 3.027 / grad: 2.967 / stop at: 0.010 : 100%|██████████| 300/300 [00:04<00:00, 66.43it/s]

Let’s compare this to the previous case.

# MixCOBRA with default parameter
print("Estimated bandwidth = {}".format(gc2_fit.optimization_outputs['opt_bandwidth']))

Estimated bandwidth = 3.0265682541599723

The learning curve.

gc2_fit.draw_learning_curve()

Copare the MSE and MAPE. Normally, using only one smoothing parameter often provides lower accuracy in prediction compared to optimizing over \((\alpha, \beta)\). However, the computational complexity is much more efficient.

from sklearn.metrics import mean_absolute_percentage_error
y_pred2 = gc2_fit.predict(X_test1)
print(mean_absolute_percentage_error(y_test1, y_pred2))
print(mean_squared_error(y_test1, y_pred2))

0.08897875460174294
62.168855511099

Let’s look at the qq-plot.

gc2_fit.draw_learning_curve(y_test=y_test1, fig_type='qq')

\(\bullet\) `MixCOBRARegressor` with non-default parameters

MixCOBRARegressor offers various options to enhance the performance of the method. By default, grid search algorithm is used to estimate the parameters \((\alpha, \beta)\), however, gradient descent algorithm can also be used to optimize the method by setting opt_method = "grad" as shown in case of one bandwidth parameter above. However, the 2D optimization with gradient descent is unstable compared to 1D case. So, it is adviced to use grid search for 2D parameter \((\alpha, \beta)\).

We create another object gc3 with non-default parameters, then fit it to the same training data as in the previous example.

import numpy as np
gc3 = MixCOBRARegressor(opt_method='grad',
                    learning_rate=0.01,
                    loss_function="weighted_mse",
                    alpha_list=np.linspace(0.001, 1, 50),
                    beta_list=np.linspace(0.001, 10, 50),
                    opt_params={
                        'start' : [0.1, 1]
                    },
                    estimator_list=['random_forest', 
                                    'adaboost', 
                                    'knn', 
                                    'svm', 
                                    'lasso', 
                                    'ridge'],
                    estimator_params={
                        'random_forest' : {
                            'n_estimators' : 300,
                            'min_samples_leaf' : 10},
                        'adaboost' : {
                            'n_estimators' : 300,
                            'max_depth' : 10},
                        'knn' : {
                            'n_neighbors' : 30},
                            'svm' : {'C' : 10}})

gc3_fit = gc3.fit(X_train1, y_train1)

* 2D-GD: iter: 0 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 0 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 0 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 1 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 1 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 2 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 2 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 3 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 3 / (a,b): (0.100,1.000) / |grad|: 47.340 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 4 / (a,b): (0.103,1.007) / |grad|: 61.921 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 4 / (a,b): (0.103,1.007) / |grad|: 61.921 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 5 / (a,b): (0.111,1.002) / |grad|: 31.146 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 5 / (a,b): (0.111,1.002) / |grad|: 31.146 / stop at: 0.010:   0%|          | 0/300 [00:00<?, ?it/s]* 2D-GD: iter: 5 / (a,b): (0.111,1.002) / |grad|: 31.146 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 6 / (a,b): (0.107,1.004) / |grad|: 38.572 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 6 / (a,b): (0.107,1.004) / |grad|: 38.572 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 7 / (a,b): (0.102,1.002) / |grad|: 87.421 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 7 / (a,b): (0.102,1.002) / |grad|: 87.421 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 8 / (a,b): (0.092,1.007) / |grad|: 37.650 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 8 / (a,b): (0.092,1.007) / |grad|: 37.650 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 9 / (a,b): (0.091,1.003) / |grad|: 47.399 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 9 / (a,b): (0.091,1.003) / |grad|: 47.399 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 10 / (a,b): (0.086,1.006) / |grad|: 47.333 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 10 / (a,b): (0.086,1.006) / |grad|: 47.333 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 11 / (a,b): (0.090,1.009) / |grad|: 4.301 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s] * 2D-GD: iter: 11 / (a,b): (0.090,1.009) / |grad|: 4.301 / stop at: 0.010:   2%|▏         | 6/300 [00:00<00:05, 51.57it/s]* 2D-GD: iter: 11 / (a,b): (0.090,1.009) / |grad|: 4.301 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 12 / (a,b): (0.089,1.008) / |grad|: 28.790 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 12 / (a,b): (0.089,1.008) / |grad|: 28.790 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 13 / (a,b): (0.090,1.011) / |grad|: 22.397 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 13 / (a,b): (0.090,1.011) / |grad|: 22.397 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 14 / (a,b): (0.088,1.012) / |grad|: 80.958 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 14 / (a,b): (0.088,1.012) / |grad|: 80.958 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 15 / (a,b): (0.095,1.014) / |grad|: 58.250 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 15 / (a,b): (0.095,1.014) / |grad|: 58.250 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 16 / (a,b): (0.096,1.010) / |grad|: 92.380 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 16 / (a,b): (0.096,1.010) / |grad|: 92.380 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 17 / (a,b): (0.106,1.011) / |grad|: 0.477 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s] * 2D-GD: iter: 17 / (a,b): (0.106,1.011) / |grad|: 0.477 / stop at: 0.010:   4%|▍         | 12/300 [00:00<00:05, 51.26it/s]* 2D-GD: iter: 17 / (a,b): (0.106,1.011) / |grad|: 0.477 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 18 / (a,b): (0.106,1.011) / |grad|: 3.600 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 18 / (a,b): (0.106,1.011) / |grad|: 3.600 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 19 / (a,b): (0.105,1.011) / |grad|: 54.579 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 19 / (a,b): (0.105,1.011) / |grad|: 54.579 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 20 / (a,b): (0.109,1.012) / |grad|: 60.533 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 20 / (a,b): (0.109,1.012) / |grad|: 60.533 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 21 / (a,b): (0.111,1.015) / |grad|: 26.670 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 21 / (a,b): (0.111,1.015) / |grad|: 26.670 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 22 / (a,b): (0.109,1.014) / |grad|: 44.323 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 22 / (a,b): (0.109,1.014) / |grad|: 44.323 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 23 / (a,b): (0.112,1.015) / |grad|: 39.066 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 23 / (a,b): (0.112,1.015) / |grad|: 39.066 / stop at: 0.010:   6%|▌         | 18/300 [00:00<00:05, 51.41it/s]* 2D-GD: iter: 23 / (a,b): (0.112,1.015) / |grad|: 39.066 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 24 / (a,b): (0.111,1.016) / |grad|: 73.253 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 24 / (a,b): (0.111,1.016) / |grad|: 73.253 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 25 / (a,b): (0.107,1.016) / |grad|: 25.645 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 25 / (a,b): (0.107,1.016) / |grad|: 25.645 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 26 / (a,b): (0.107,1.017) / |grad|: 89.986 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 26 / (a,b): (0.107,1.017) / |grad|: 89.986 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 27 / (a,b): (0.109,1.015) / |grad|: 32.323 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 27 / (a,b): (0.109,1.015) / |grad|: 32.323 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 28 / (a,b): (0.109,1.014) / |grad|: 7.430 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s] * 2D-GD: iter: 28 / (a,b): (0.109,1.014) / |grad|: 7.430 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 29 / (a,b): (0.109,1.014) / |grad|: 18.042 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 29 / (a,b): (0.109,1.014) / |grad|: 18.042 / stop at: 0.010:   8%|▊         | 24/300 [00:00<00:05, 51.53it/s]* 2D-GD: iter: 29 / (a,b): (0.109,1.014) / |grad|: 18.042 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 30 / (a,b): (0.110,1.014) / |grad|: 121.159 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 30 / (a,b): (0.110,1.014) / |grad|: 121.159 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 31 / (a,b): (0.114,1.016) / |grad|: 67.772 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s] * 2D-GD: iter: 31 / (a,b): (0.114,1.016) / |grad|: 67.772 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 32 / (a,b): (0.113,1.014) / |grad|: 41.724 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 32 / (a,b): (0.113,1.014) / |grad|: 41.724 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 33 / (a,b): (0.113,1.015) / |grad|: 59.050 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 33 / (a,b): (0.113,1.015) / |grad|: 59.050 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 34 / (a,b): (0.115,1.016) / |grad|: 21.829 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 34 / (a,b): (0.115,1.016) / |grad|: 21.829 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 35 / (a,b): (0.115,1.015) / |grad|: 85.935 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 35 / (a,b): (0.115,1.015) / |grad|: 85.935 / stop at: 0.010:  10%|█         | 30/300 [00:00<00:05, 48.84it/s]* 2D-GD: iter: 35 / (a,b): (0.115,1.015) / |grad|: 85.935 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 36 / (a,b): (0.113,1.016) / |grad|: 31.033 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 36 / (a,b): (0.113,1.016) / |grad|: 31.033 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 37 / (a,b): (0.113,1.017) / |grad|: 39.807 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 37 / (a,b): (0.113,1.017) / |grad|: 39.807 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 38 / (a,b): (0.114,1.018) / |grad|: 74.095 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 38 / (a,b): (0.114,1.018) / |grad|: 74.095 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 39 / (a,b): (0.112,1.018) / |grad|: 37.223 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 39 / (a,b): (0.112,1.018) / |grad|: 37.223 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 40 / (a,b): (0.112,1.019) / |grad|: 84.328 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 40 / (a,b): (0.112,1.019) / |grad|: 84.328 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 41 / (a,b): (0.111,1.018) / |grad|: 50.999 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 41 / (a,b): (0.111,1.018) / |grad|: 50.999 / stop at: 0.010:  12%|█▏        | 36/300 [00:00<00:05, 49.82it/s]* 2D-GD: iter: 41 / (a,b): (0.111,1.018) / |grad|: 50.999 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 42 / (a,b): (0.111,1.018) / |grad|: 17.812 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 42 / (a,b): (0.111,1.018) / |grad|: 17.812 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 43 / (a,b): (0.111,1.018) / |grad|: 7.861 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s] * 2D-GD: iter: 43 / (a,b): (0.111,1.018) / |grad|: 7.861 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 44 / (a,b): (0.111,1.018) / |grad|: 62.248 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 44 / (a,b): (0.111,1.018) / |grad|: 62.248 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 45 / (a,b): (0.111,1.019) / |grad|: 26.239 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 45 / (a,b): (0.111,1.019) / |grad|: 26.239 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 46 / (a,b): (0.112,1.019) / |grad|: 55.636 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 46 / (a,b): (0.112,1.019) / |grad|: 55.636 / stop at: 0.010:  14%|█▍        | 42/300 [00:00<00:05, 48.09it/s]* 2D-GD: iter: 46 / (a,b): (0.112,1.019) / |grad|: 55.636 / stop at: 0.010:  16%|█▌        | 47/300 [00:00<00:05, 48.59it/s]* 2D-GD: iter: 47 / (a,b): (0.111,1.019) / |grad|: 60.513 / stop at: 0.010:  16%|█▌        | 47/300 [00:00<00:05, 48.59it/s]* 2D-GD: iter: 47 / (a,b): (0.111,1.019) / |grad|: 60.513 / stop at: 0.010:  16%|█▌        | 47/300 [00:00<00:05, 48.59it/s]* 2D-GD: iter: 48 / (a,b): (0.110,1.019) / |grad|: 27.485 / stop at: 0.010:  16%|█▌        | 47/300 [00:00<00:05, 48.59it/s]* 2D-GD: iter: 48 / (a,b): (0.110,1.019) / |grad|: 27.485 / stop at: 0.010:  16%|█▌        | 47/300 [00:00<00:05, 48.59it/s]* 2D-GD: iter: 49 / (a,b): (0.110,1.018) / |grad|: 28.430 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 49 / (a,b): (0.110,1.018) / |grad|: 28.430 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 50 / (a,b): (0.110,1.019) / |grad|: 31.689 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 50 / (a,b): (0.110,1.019) / |grad|: 31.689 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 51 / (a,b): (0.110,1.019) / |grad|: 34.391 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 51 / (a,b): (0.110,1.019) / |grad|: 34.391 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 52 / (a,b): (0.110,1.019) / |grad|: 18.218 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 52 / (a,b): (0.110,1.019) / |grad|: 18.218 / stop at: 0.010:  16%|█▌        | 47/300 [00:01<00:05, 48.59it/s]* 2D-GD: iter: 52 / (a,b): (0.110,1.019) / |grad|: 18.218 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 53 / (a,b): (0.109,1.019) / |grad|: 35.118 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 53 / (a,b): (0.109,1.019) / |grad|: 35.118 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 54 / (a,b): (0.109,1.019) / |grad|: 38.558 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 54 / (a,b): (0.109,1.019) / |grad|: 38.558 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 55 / (a,b): (0.109,1.019) / |grad|: 45.168 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 55 / (a,b): (0.109,1.019) / |grad|: 45.168 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 56 / (a,b): (0.109,1.019) / |grad|: 36.915 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 56 / (a,b): (0.109,1.019) / |grad|: 36.915 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 57 / (a,b): (0.109,1.019) / |grad|: 52.411 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 57 / (a,b): (0.109,1.019) / |grad|: 52.411 / stop at: 0.010:  18%|█▊        | 53/300 [00:01<00:04, 49.54it/s]* 2D-GD: iter: 57 / (a,b): (0.109,1.019) / |grad|: 52.411 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 58 / (a,b): (0.109,1.019) / |grad|: 41.747 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 58 / (a,b): (0.109,1.019) / |grad|: 41.747 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 59 / (a,b): (0.109,1.019) / |grad|: 58.906 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 59 / (a,b): (0.109,1.019) / |grad|: 58.906 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 60 / (a,b): (0.109,1.019) / |grad|: 33.366 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 60 / (a,b): (0.109,1.019) / |grad|: 33.366 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 61 / (a,b): (0.109,1.019) / |grad|: 46.293 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 61 / (a,b): (0.109,1.019) / |grad|: 46.293 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 62 / (a,b): (0.109,1.019) / |grad|: 22.925 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 62 / (a,b): (0.109,1.019) / |grad|: 22.925 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 63 / (a,b): (0.109,1.019) / |grad|: 22.877 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 63 / (a,b): (0.109,1.019) / |grad|: 22.877 / stop at: 0.010:  19%|█▉        | 58/300 [00:01<00:04, 49.65it/s]* 2D-GD: iter: 63 / (a,b): (0.109,1.019) / |grad|: 22.877 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 64 / (a,b): (0.109,1.019) / |grad|: 34.392 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 64 / (a,b): (0.109,1.019) / |grad|: 34.392 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 65 / (a,b): (0.109,1.020) / |grad|: 31.153 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 65 / (a,b): (0.109,1.020) / |grad|: 31.153 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 66 / (a,b): (0.109,1.020) / |grad|: 53.761 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 66 / (a,b): (0.109,1.020) / |grad|: 53.761 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 67 / (a,b): (0.109,1.020) / |grad|: 9.869 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s] * 2D-GD: iter: 67 / (a,b): (0.109,1.020) / |grad|: 9.869 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 68 / (a,b): (0.109,1.020) / |grad|: 51.796 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 68 / (a,b): (0.109,1.020) / |grad|: 51.796 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 69 / (a,b): (0.109,1.020) / |grad|: 115.328 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 69 / (a,b): (0.109,1.020) / |grad|: 115.328 / stop at: 0.010:  21%|██▏       | 64/300 [00:01<00:04, 50.21it/s]* 2D-GD: iter: 69 / (a,b): (0.109,1.020) / |grad|: 115.328 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 70 / (a,b): (0.108,1.020) / |grad|: 32.153 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s] * 2D-GD: iter: 70 / (a,b): (0.108,1.020) / |grad|: 32.153 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 71 / (a,b): (0.108,1.020) / |grad|: 54.984 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 71 / (a,b): (0.108,1.020) / |grad|: 54.984 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 72 / (a,b): (0.108,1.020) / |grad|: 34.244 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 72 / (a,b): (0.108,1.020) / |grad|: 34.244 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 73 / (a,b): (0.108,1.020) / |grad|: 37.413 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 73 / (a,b): (0.108,1.020) / |grad|: 37.413 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 74 / (a,b): (0.108,1.020) / |grad|: 89.948 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 74 / (a,b): (0.108,1.020) / |grad|: 89.948 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 75 / (a,b): (0.108,1.020) / |grad|: 62.737 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 75 / (a,b): (0.108,1.020) / |grad|: 62.737 / stop at: 0.010:  23%|██▎       | 70/300 [00:01<00:04, 48.45it/s]* 2D-GD: iter: 75 / (a,b): (0.108,1.020) / |grad|: 62.737 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 76 / (a,b): (0.108,1.020) / |grad|: 78.078 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 76 / (a,b): (0.108,1.020) / |grad|: 78.078 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 77 / (a,b): (0.109,1.019) / |grad|: 50.821 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 77 / (a,b): (0.109,1.019) / |grad|: 50.821 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 78 / (a,b): (0.109,1.020) / |grad|: 13.270 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 78 / (a,b): (0.109,1.020) / |grad|: 13.270 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 79 / (a,b): (0.109,1.020) / |grad|: 69.767 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 79 / (a,b): (0.109,1.020) / |grad|: 69.767 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 80 / (a,b): (0.109,1.019) / |grad|: 31.017 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 80 / (a,b): (0.109,1.019) / |grad|: 31.017 / stop at: 0.010:  25%|██▌       | 76/300 [00:01<00:04, 49.35it/s]* 2D-GD: iter: 80 / (a,b): (0.109,1.019) / |grad|: 31.017 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 81 / (a,b): (0.108,1.020) / |grad|: 66.285 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 81 / (a,b): (0.108,1.020) / |grad|: 66.285 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 82 / (a,b): (0.108,1.020) / |grad|: 59.461 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 82 / (a,b): (0.108,1.020) / |grad|: 59.461 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 83 / (a,b): (0.109,1.020) / |grad|: 54.050 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 83 / (a,b): (0.109,1.020) / |grad|: 54.050 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 84 / (a,b): (0.109,1.020) / |grad|: 32.029 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 84 / (a,b): (0.109,1.020) / |grad|: 32.029 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 85 / (a,b): (0.109,1.020) / |grad|: 77.633 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 85 / (a,b): (0.109,1.020) / |grad|: 77.633 / stop at: 0.010:  27%|██▋       | 81/300 [00:01<00:04, 47.52it/s]* 2D-GD: iter: 85 / (a,b): (0.109,1.020) / |grad|: 77.633 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 86 / (a,b): (0.109,1.020) / |grad|: 46.344 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 86 / (a,b): (0.109,1.020) / |grad|: 46.344 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 87 / (a,b): (0.109,1.020) / |grad|: 48.398 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 87 / (a,b): (0.109,1.020) / |grad|: 48.398 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 88 / (a,b): (0.109,1.020) / |grad|: 80.312 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 88 / (a,b): (0.109,1.020) / |grad|: 80.312 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 89 / (a,b): (0.109,1.020) / |grad|: 43.592 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 89 / (a,b): (0.109,1.020) / |grad|: 43.592 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 90 / (a,b): (0.109,1.020) / |grad|: 24.901 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 90 / (a,b): (0.109,1.020) / |grad|: 24.901 / stop at: 0.010:  29%|██▊       | 86/300 [00:01<00:04, 46.00it/s]* 2D-GD: iter: 90 / (a,b): (0.109,1.020) / |grad|: 24.901 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 91 / (a,b): (0.109,1.020) / |grad|: 58.169 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 91 / (a,b): (0.109,1.020) / |grad|: 58.169 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 92 / (a,b): (0.109,1.020) / |grad|: 20.555 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 92 / (a,b): (0.109,1.020) / |grad|: 20.555 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 93 / (a,b): (0.109,1.020) / |grad|: 21.355 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 93 / (a,b): (0.109,1.020) / |grad|: 21.355 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 94 / (a,b): (0.109,1.020) / |grad|: 86.556 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 94 / (a,b): (0.109,1.020) / |grad|: 86.556 / stop at: 0.010:  30%|███       | 91/300 [00:01<00:04, 45.05it/s]* 2D-GD: iter: 95 / (a,b): (0.109,1.020) / |grad|: 43.012 / stop at: 0.010:  30%|███       | 91/300 [00:02<00:04, 45.05it/s]* 2D-GD: iter: 95 / (a,b): (0.109,1.020) / |grad|: 43.012 / stop at: 0.010:  30%|███       | 91/300 [00:02<00:04, 45.05it/s]* 2D-GD: iter: 95 / (a,b): (0.109,1.020) / |grad|: 43.012 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 96 / (a,b): (0.109,1.020) / |grad|: 21.878 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 96 / (a,b): (0.109,1.020) / |grad|: 21.878 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 97 / (a,b): (0.109,1.020) / |grad|: 25.534 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 97 / (a,b): (0.109,1.020) / |grad|: 25.534 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 98 / (a,b): (0.109,1.020) / |grad|: 107.313 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 98 / (a,b): (0.109,1.020) / |grad|: 107.313 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 99 / (a,b): (0.109,1.020) / |grad|: 89.928 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s] * 2D-GD: iter: 99 / (a,b): (0.109,1.020) / |grad|: 89.928 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 100 / (a,b): (0.109,1.020) / |grad|: 33.577 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 100 / (a,b): (0.109,1.020) / |grad|: 33.577 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 101 / (a,b): (0.109,1.020) / |grad|: 59.387 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 101 / (a,b): (0.109,1.020) / |grad|: 59.387 / stop at: 0.010:  32%|███▏      | 96/300 [00:02<00:04, 42.47it/s]* 2D-GD: iter: 101 / (a,b): (0.109,1.020) / |grad|: 59.387 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 102 / (a,b): (0.109,1.020) / |grad|: 36.058 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 102 / (a,b): (0.109,1.020) / |grad|: 36.058 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 103 / (a,b): (0.109,1.020) / |grad|: 51.541 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 103 / (a,b): (0.109,1.020) / |grad|: 51.541 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 104 / (a,b): (0.109,1.020) / |grad|: 27.168 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 104 / (a,b): (0.109,1.020) / |grad|: 27.168 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 105 / (a,b): (0.109,1.020) / |grad|: 96.769 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 105 / (a,b): (0.109,1.020) / |grad|: 96.769 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 106 / (a,b): (0.109,1.020) / |grad|: 67.034 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 106 / (a,b): (0.109,1.020) / |grad|: 67.034 / stop at: 0.010:  34%|███▍      | 102/300 [00:02<00:04, 45.18it/s]* 2D-GD: iter: 106 / (a,b): (0.109,1.020) / |grad|: 67.034 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 107 / (a,b): (0.109,1.020) / |grad|: 56.385 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 107 / (a,b): (0.109,1.020) / |grad|: 56.385 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 108 / (a,b): (0.109,1.020) / |grad|: 69.420 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 108 / (a,b): (0.109,1.020) / |grad|: 69.420 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 109 / (a,b): (0.109,1.020) / |grad|: 61.143 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 109 / (a,b): (0.109,1.020) / |grad|: 61.143 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 110 / (a,b): (0.109,1.020) / |grad|: 51.519 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 110 / (a,b): (0.109,1.020) / |grad|: 51.519 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 111 / (a,b): (0.109,1.020) / |grad|: 14.801 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 111 / (a,b): (0.109,1.020) / |grad|: 14.801 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 112 / (a,b): (0.109,1.020) / |grad|: 24.151 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 112 / (a,b): (0.109,1.020) / |grad|: 24.151 / stop at: 0.010:  36%|███▌      | 107/300 [00:02<00:04, 46.36it/s]* 2D-GD: iter: 112 / (a,b): (0.109,1.020) / |grad|: 24.151 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 113 / (a,b): (0.109,1.020) / |grad|: 42.334 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 113 / (a,b): (0.109,1.020) / |grad|: 42.334 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 114 / (a,b): (0.109,1.020) / |grad|: 92.564 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 114 / (a,b): (0.109,1.020) / |grad|: 92.564 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 115 / (a,b): (0.109,1.020) / |grad|: 27.597 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 115 / (a,b): (0.109,1.020) / |grad|: 27.597 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 116 / (a,b): (0.109,1.020) / |grad|: 60.184 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 116 / (a,b): (0.109,1.020) / |grad|: 60.184 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 117 / (a,b): (0.109,1.020) / |grad|: 67.662 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 117 / (a,b): (0.109,1.020) / |grad|: 67.662 / stop at: 0.010:  38%|███▊      | 113/300 [00:02<00:04, 46.07it/s]* 2D-GD: iter: 117 / (a,b): (0.109,1.020) / |grad|: 67.662 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 118 / (a,b): (0.109,1.020) / |grad|: 42.705 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 118 / (a,b): (0.109,1.020) / |grad|: 42.705 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 119 / (a,b): (0.109,1.020) / |grad|: 16.863 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 119 / (a,b): (0.109,1.020) / |grad|: 16.863 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 120 / (a,b): (0.109,1.020) / |grad|: 43.839 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 120 / (a,b): (0.109,1.020) / |grad|: 43.839 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 121 / (a,b): (0.109,1.020) / |grad|: 45.397 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 121 / (a,b): (0.109,1.020) / |grad|: 45.397 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 122 / (a,b): (0.109,1.020) / |grad|: 34.958 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 122 / (a,b): (0.109,1.020) / |grad|: 34.958 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 123 / (a,b): (0.109,1.020) / |grad|: 44.092 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 123 / (a,b): (0.109,1.020) / |grad|: 44.092 / stop at: 0.010:  39%|███▉      | 118/300 [00:02<00:03, 47.02it/s]* 2D-GD: iter: 123 / (a,b): (0.109,1.020) / |grad|: 44.092 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 124 / (a,b): (0.109,1.020) / |grad|: 18.669 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 124 / (a,b): (0.109,1.020) / |grad|: 18.669 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 125 / (a,b): (0.109,1.020) / |grad|: 43.443 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 125 / (a,b): (0.109,1.020) / |grad|: 43.443 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 126 / (a,b): (0.109,1.020) / |grad|: 38.222 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 126 / (a,b): (0.109,1.020) / |grad|: 38.222 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 127 / (a,b): (0.109,1.020) / |grad|: 75.478 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 127 / (a,b): (0.109,1.020) / |grad|: 75.478 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 128 / (a,b): (0.109,1.020) / |grad|: 44.155 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 128 / (a,b): (0.109,1.020) / |grad|: 44.155 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 129 / (a,b): (0.109,1.020) / |grad|: 21.783 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 129 / (a,b): (0.109,1.020) / |grad|: 21.783 / stop at: 0.010:  41%|████▏     | 124/300 [00:02<00:03, 48.40it/s]* 2D-GD: iter: 129 / (a,b): (0.109,1.020) / |grad|: 21.783 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 130 / (a,b): (0.109,1.020) / |grad|: 44.455 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 130 / (a,b): (0.109,1.020) / |grad|: 44.455 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 131 / (a,b): (0.109,1.020) / |grad|: 33.606 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 131 / (a,b): (0.109,1.020) / |grad|: 33.606 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 132 / (a,b): (0.109,1.020) / |grad|: 61.917 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 132 / (a,b): (0.109,1.020) / |grad|: 61.917 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 133 / (a,b): (0.109,1.020) / |grad|: 53.619 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 133 / (a,b): (0.109,1.020) / |grad|: 53.619 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 134 / (a,b): (0.109,1.020) / |grad|: 74.335 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 134 / (a,b): (0.109,1.020) / |grad|: 74.335 / stop at: 0.010:  43%|████▎     | 130/300 [00:02<00:03, 49.25it/s]* 2D-GD: iter: 134 / (a,b): (0.109,1.020) / |grad|: 74.335 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 135 / (a,b): (0.109,1.020) / |grad|: 58.094 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 135 / (a,b): (0.109,1.020) / |grad|: 58.094 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 136 / (a,b): (0.109,1.020) / |grad|: 25.571 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 136 / (a,b): (0.109,1.020) / |grad|: 25.571 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 137 / (a,b): (0.109,1.020) / |grad|: 10.810 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 137 / (a,b): (0.109,1.020) / |grad|: 10.810 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 138 / (a,b): (0.109,1.020) / |grad|: 32.852 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 138 / (a,b): (0.109,1.020) / |grad|: 32.852 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 139 / (a,b): (0.109,1.020) / |grad|: 36.848 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 139 / (a,b): (0.109,1.020) / |grad|: 36.848 / stop at: 0.010:  45%|████▌     | 135/300 [00:02<00:03, 49.42it/s]* 2D-GD: iter: 139 / (a,b): (0.109,1.020) / |grad|: 36.848 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 140 / (a,b): (0.109,1.020) / |grad|: 90.994 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 140 / (a,b): (0.109,1.020) / |grad|: 90.994 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 141 / (a,b): (0.109,1.020) / |grad|: 77.341 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 141 / (a,b): (0.109,1.020) / |grad|: 77.341 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 142 / (a,b): (0.109,1.020) / |grad|: 23.210 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 142 / (a,b): (0.109,1.020) / |grad|: 23.210 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 143 / (a,b): (0.109,1.020) / |grad|: 40.254 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 143 / (a,b): (0.109,1.020) / |grad|: 40.254 / stop at: 0.010:  47%|████▋     | 140/300 [00:02<00:03, 47.45it/s]* 2D-GD: iter: 144 / (a,b): (0.109,1.020) / |grad|: 20.631 / stop at: 0.010:  47%|████▋     | 140/300 [00:03<00:03, 47.45it/s]* 2D-GD: iter: 144 / (a,b): (0.109,1.020) / |grad|: 20.631 / stop at: 0.010:  47%|████▋     | 140/300 [00:03<00:03, 47.45it/s]* 2D-GD: iter: 144 / (a,b): (0.109,1.020) / |grad|: 20.631 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 145 / (a,b): (0.109,1.020) / |grad|: 46.759 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 145 / (a,b): (0.109,1.020) / |grad|: 46.759 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 146 / (a,b): (0.109,1.020) / |grad|: 39.102 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 146 / (a,b): (0.109,1.020) / |grad|: 39.102 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 147 / (a,b): (0.109,1.020) / |grad|: 93.195 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 147 / (a,b): (0.109,1.020) / |grad|: 93.195 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 148 / (a,b): (0.109,1.020) / |grad|: 37.226 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 148 / (a,b): (0.109,1.020) / |grad|: 37.226 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 149 / (a,b): (0.109,1.020) / |grad|: 44.626 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 149 / (a,b): (0.109,1.020) / |grad|: 44.626 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 150 / (a,b): (0.109,1.020) / |grad|: 45.155 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 150 / (a,b): (0.109,1.020) / |grad|: 45.155 / stop at: 0.010:  48%|████▊     | 145/300 [00:03<00:03, 48.15it/s]* 2D-GD: iter: 150 / (a,b): (0.109,1.020) / |grad|: 45.155 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 151 / (a,b): (0.109,1.020) / |grad|: 41.977 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 151 / (a,b): (0.109,1.020) / |grad|: 41.977 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 152 / (a,b): (0.109,1.020) / |grad|: 29.381 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 152 / (a,b): (0.109,1.020) / |grad|: 29.381 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 153 / (a,b): (0.109,1.020) / |grad|: 59.950 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 153 / (a,b): (0.109,1.020) / |grad|: 59.950 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 154 / (a,b): (0.109,1.020) / |grad|: 30.995 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 154 / (a,b): (0.109,1.020) / |grad|: 30.995 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 155 / (a,b): (0.109,1.020) / |grad|: 41.130 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 155 / (a,b): (0.109,1.020) / |grad|: 41.130 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 156 / (a,b): (0.109,1.020) / |grad|: 57.693 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 156 / (a,b): (0.109,1.020) / |grad|: 57.693 / stop at: 0.010:  50%|█████     | 151/300 [00:03<00:03, 49.21it/s]* 2D-GD: iter: 156 / (a,b): (0.109,1.020) / |grad|: 57.693 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 157 / (a,b): (0.109,1.020) / |grad|: 48.137 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 157 / (a,b): (0.109,1.020) / |grad|: 48.137 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 158 / (a,b): (0.109,1.020) / |grad|: 69.745 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 158 / (a,b): (0.109,1.020) / |grad|: 69.745 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 159 / (a,b): (0.109,1.020) / |grad|: 65.904 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 159 / (a,b): (0.109,1.020) / |grad|: 65.904 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 160 / (a,b): (0.109,1.020) / |grad|: 17.875 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 160 / (a,b): (0.109,1.020) / |grad|: 17.875 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 161 / (a,b): (0.109,1.020) / |grad|: 47.233 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 161 / (a,b): (0.109,1.020) / |grad|: 47.233 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 162 / (a,b): (0.109,1.020) / |grad|: 31.015 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 162 / (a,b): (0.109,1.020) / |grad|: 31.015 / stop at: 0.010:  52%|█████▏    | 157/300 [00:03<00:02, 52.21it/s]* 2D-GD: iter: 162 / (a,b): (0.109,1.020) / |grad|: 31.015 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 163 / (a,b): (0.109,1.020) / |grad|: 35.258 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 163 / (a,b): (0.109,1.020) / |grad|: 35.258 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 164 / (a,b): (0.109,1.020) / |grad|: 43.369 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 164 / (a,b): (0.109,1.020) / |grad|: 43.369 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 165 / (a,b): (0.109,1.020) / |grad|: 73.218 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 165 / (a,b): (0.109,1.020) / |grad|: 73.218 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 166 / (a,b): (0.109,1.020) / |grad|: 40.133 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 166 / (a,b): (0.109,1.020) / |grad|: 40.133 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 167 / (a,b): (0.109,1.020) / |grad|: 57.737 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 167 / (a,b): (0.109,1.020) / |grad|: 57.737 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 168 / (a,b): (0.109,1.020) / |grad|: 51.489 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 168 / (a,b): (0.109,1.020) / |grad|: 51.489 / stop at: 0.010:  54%|█████▍    | 163/300 [00:03<00:02, 51.91it/s]* 2D-GD: iter: 168 / (a,b): (0.109,1.020) / |grad|: 51.489 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 169 / (a,b): (0.109,1.020) / |grad|: 29.147 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 169 / (a,b): (0.109,1.020) / |grad|: 29.147 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 170 / (a,b): (0.109,1.020) / |grad|: 51.534 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 170 / (a,b): (0.109,1.020) / |grad|: 51.534 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 171 / (a,b): (0.109,1.020) / |grad|: 76.636 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 171 / (a,b): (0.109,1.020) / |grad|: 76.636 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 172 / (a,b): (0.109,1.020) / |grad|: 27.058 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 172 / (a,b): (0.109,1.020) / |grad|: 27.058 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 173 / (a,b): (0.109,1.020) / |grad|: 41.399 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 173 / (a,b): (0.109,1.020) / |grad|: 41.399 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 174 / (a,b): (0.109,1.020) / |grad|: 17.134 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 174 / (a,b): (0.109,1.020) / |grad|: 17.134 / stop at: 0.010:  56%|█████▋    | 169/300 [00:03<00:02, 51.80it/s]* 2D-GD: iter: 174 / (a,b): (0.109,1.020) / |grad|: 17.134 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 175 / (a,b): (0.109,1.020) / |grad|: 63.593 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 175 / (a,b): (0.109,1.020) / |grad|: 63.593 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 176 / (a,b): (0.109,1.020) / |grad|: 22.481 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 176 / (a,b): (0.109,1.020) / |grad|: 22.481 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 177 / (a,b): (0.109,1.020) / |grad|: 33.811 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 177 / (a,b): (0.109,1.020) / |grad|: 33.811 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 178 / (a,b): (0.109,1.020) / |grad|: 27.377 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 178 / (a,b): (0.109,1.020) / |grad|: 27.377 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 179 / (a,b): (0.109,1.020) / |grad|: 28.701 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 179 / (a,b): (0.109,1.020) / |grad|: 28.701 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 180 / (a,b): (0.109,1.020) / |grad|: 51.253 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 180 / (a,b): (0.109,1.020) / |grad|: 51.253 / stop at: 0.010:  58%|█████▊    | 175/300 [00:03<00:02, 53.86it/s]* 2D-GD: iter: 180 / (a,b): (0.109,1.020) / |grad|: 51.253 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 181 / (a,b): (0.109,1.020) / |grad|: 8.964 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s] * 2D-GD: iter: 181 / (a,b): (0.109,1.020) / |grad|: 8.964 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 182 / (a,b): (0.109,1.020) / |grad|: 40.561 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 182 / (a,b): (0.109,1.020) / |grad|: 40.561 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 183 / (a,b): (0.109,1.020) / |grad|: 56.333 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 183 / (a,b): (0.109,1.020) / |grad|: 56.333 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 184 / (a,b): (0.109,1.020) / |grad|: 44.482 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 184 / (a,b): (0.109,1.020) / |grad|: 44.482 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 185 / (a,b): (0.109,1.020) / |grad|: 46.715 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 185 / (a,b): (0.109,1.020) / |grad|: 46.715 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 186 / (a,b): (0.109,1.020) / |grad|: 54.285 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 186 / (a,b): (0.109,1.020) / |grad|: 54.285 / stop at: 0.010:  60%|██████    | 181/300 [00:03<00:02, 53.29it/s]* 2D-GD: iter: 186 / (a,b): (0.109,1.020) / |grad|: 54.285 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 187 / (a,b): (0.109,1.020) / |grad|: 20.680 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 187 / (a,b): (0.109,1.020) / |grad|: 20.680 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 188 / (a,b): (0.109,1.020) / |grad|: 16.256 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 188 / (a,b): (0.109,1.020) / |grad|: 16.256 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 189 / (a,b): (0.109,1.020) / |grad|: 41.004 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 189 / (a,b): (0.109,1.020) / |grad|: 41.004 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 190 / (a,b): (0.109,1.020) / |grad|: 52.226 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 190 / (a,b): (0.109,1.020) / |grad|: 52.226 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 191 / (a,b): (0.109,1.020) / |grad|: 36.979 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 191 / (a,b): (0.109,1.020) / |grad|: 36.979 / stop at: 0.010:  62%|██████▏   | 187/300 [00:03<00:02, 48.43it/s]* 2D-GD: iter: 191 / (a,b): (0.109,1.020) / |grad|: 36.979 / stop at: 0.010:  64%|██████▍   | 192/300 [00:03<00:02, 46.73it/s]* 2D-GD: iter: 192 / (a,b): (0.109,1.020) / |grad|: 66.108 / stop at: 0.010:  64%|██████▍   | 192/300 [00:03<00:02, 46.73it/s]* 2D-GD: iter: 192 / (a,b): (0.109,1.020) / |grad|: 66.108 / stop at: 0.010:  64%|██████▍   | 192/300 [00:03<00:02, 46.73it/s]* 2D-GD: iter: 193 / (a,b): (0.109,1.020) / |grad|: 55.481 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 193 / (a,b): (0.109,1.020) / |grad|: 55.481 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 194 / (a,b): (0.109,1.020) / |grad|: 87.424 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 194 / (a,b): (0.109,1.020) / |grad|: 87.424 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 195 / (a,b): (0.109,1.020) / |grad|: 32.822 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 195 / (a,b): (0.109,1.020) / |grad|: 32.822 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 196 / (a,b): (0.109,1.020) / |grad|: 63.654 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 196 / (a,b): (0.109,1.020) / |grad|: 63.654 / stop at: 0.010:  64%|██████▍   | 192/300 [00:04<00:02, 46.73it/s]* 2D-GD: iter: 196 / (a,b): (0.109,1.020) / |grad|: 63.654 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 197 / (a,b): (0.109,1.020) / |grad|: 129.545 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 197 / (a,b): (0.109,1.020) / |grad|: 129.545 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 198 / (a,b): (0.109,1.020) / |grad|: 109.878 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 198 / (a,b): (0.109,1.020) / |grad|: 109.878 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 199 / (a,b): (0.109,1.020) / |grad|: 89.924 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s] * 2D-GD: iter: 199 / (a,b): (0.109,1.020) / |grad|: 89.924 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 200 / (a,b): (0.109,1.020) / |grad|: 63.894 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 200 / (a,b): (0.109,1.020) / |grad|: 63.894 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 201 / (a,b): (0.109,1.020) / |grad|: 96.620 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 201 / (a,b): (0.109,1.020) / |grad|: 96.620 / stop at: 0.010:  66%|██████▌   | 197/300 [00:04<00:02, 43.71it/s]* 2D-GD: iter: 201 / (a,b): (0.109,1.020) / |grad|: 96.620 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 202 / (a,b): (0.109,1.020) / |grad|: 35.699 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 202 / (a,b): (0.109,1.020) / |grad|: 35.699 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 203 / (a,b): (0.109,1.020) / |grad|: 22.128 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 203 / (a,b): (0.109,1.020) / |grad|: 22.128 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 204 / (a,b): (0.109,1.020) / |grad|: 10.031 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 204 / (a,b): (0.109,1.020) / |grad|: 10.031 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 205 / (a,b): (0.109,1.020) / |grad|: 34.801 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 205 / (a,b): (0.109,1.020) / |grad|: 34.801 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 206 / (a,b): (0.109,1.020) / |grad|: 16.364 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 206 / (a,b): (0.109,1.020) / |grad|: 16.364 / stop at: 0.010:  67%|██████▋   | 202/300 [00:04<00:02, 43.78it/s]* 2D-GD: iter: 206 / (a,b): (0.109,1.020) / |grad|: 16.364 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 207 / (a,b): (0.109,1.020) / |grad|: 19.710 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 207 / (a,b): (0.109,1.020) / |grad|: 19.710 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 208 / (a,b): (0.109,1.020) / |grad|: 12.480 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 208 / (a,b): (0.109,1.020) / |grad|: 12.480 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 209 / (a,b): (0.109,1.020) / |grad|: 34.471 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 209 / (a,b): (0.109,1.020) / |grad|: 34.471 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 210 / (a,b): (0.109,1.020) / |grad|: 31.445 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 210 / (a,b): (0.109,1.020) / |grad|: 31.445 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 211 / (a,b): (0.109,1.020) / |grad|: 63.998 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 211 / (a,b): (0.109,1.020) / |grad|: 63.998 / stop at: 0.010:  69%|██████▉   | 207/300 [00:04<00:02, 43.32it/s]* 2D-GD: iter: 211 / (a,b): (0.109,1.020) / |grad|: 63.998 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 212 / (a,b): (0.109,1.020) / |grad|: 38.036 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 212 / (a,b): (0.109,1.020) / |grad|: 38.036 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 213 / (a,b): (0.109,1.020) / |grad|: 32.532 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 213 / (a,b): (0.109,1.020) / |grad|: 32.532 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 214 / (a,b): (0.109,1.020) / |grad|: 44.706 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 214 / (a,b): (0.109,1.020) / |grad|: 44.706 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 215 / (a,b): (0.109,1.020) / |grad|: 33.870 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 215 / (a,b): (0.109,1.020) / |grad|: 33.870 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 216 / (a,b): (0.109,1.020) / |grad|: 26.602 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 216 / (a,b): (0.109,1.020) / |grad|: 26.602 / stop at: 0.010:  71%|███████   | 212/300 [00:04<00:02, 43.17it/s]* 2D-GD: iter: 216 / (a,b): (0.109,1.020) / |grad|: 26.602 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 217 / (a,b): (0.109,1.020) / |grad|: 6.641 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s] * 2D-GD: iter: 217 / (a,b): (0.109,1.020) / |grad|: 6.641 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 218 / (a,b): (0.109,1.020) / |grad|: 55.380 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 218 / (a,b): (0.109,1.020) / |grad|: 55.380 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 219 / (a,b): (0.109,1.020) / |grad|: 13.185 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 219 / (a,b): (0.109,1.020) / |grad|: 13.185 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 220 / (a,b): (0.109,1.020) / |grad|: 3.064 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s] * 2D-GD: iter: 220 / (a,b): (0.109,1.020) / |grad|: 3.064 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 221 / (a,b): (0.109,1.020) / |grad|: 5.309 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 221 / (a,b): (0.109,1.020) / |grad|: 5.309 / stop at: 0.010:  72%|███████▏  | 217/300 [00:04<00:01, 43.03it/s]* 2D-GD: iter: 221 / (a,b): (0.109,1.020) / |grad|: 5.309 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 222 / (a,b): (0.109,1.020) / |grad|: 6.286 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 222 / (a,b): (0.109,1.020) / |grad|: 6.286 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 223 / (a,b): (0.109,1.020) / |grad|: 4.046 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 223 / (a,b): (0.109,1.020) / |grad|: 4.046 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 224 / (a,b): (0.109,1.020) / |grad|: 12.419 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 224 / (a,b): (0.109,1.020) / |grad|: 12.419 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 225 / (a,b): (0.109,1.020) / |grad|: 30.714 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 225 / (a,b): (0.109,1.020) / |grad|: 30.714 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 226 / (a,b): (0.109,1.020) / |grad|: 15.943 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 226 / (a,b): (0.109,1.020) / |grad|: 15.943 / stop at: 0.010:  74%|███████▍  | 222/300 [00:04<00:01, 44.86it/s]* 2D-GD: iter: 226 / (a,b): (0.109,1.020) / |grad|: 15.943 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 227 / (a,b): (0.109,1.020) / |grad|: 14.221 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 227 / (a,b): (0.109,1.020) / |grad|: 14.221 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 228 / (a,b): (0.109,1.020) / |grad|: 13.673 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 228 / (a,b): (0.109,1.020) / |grad|: 13.673 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 229 / (a,b): (0.109,1.020) / |grad|: 18.771 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 229 / (a,b): (0.109,1.020) / |grad|: 18.771 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 230 / (a,b): (0.109,1.020) / |grad|: 17.739 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 230 / (a,b): (0.109,1.020) / |grad|: 17.739 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 231 / (a,b): (0.109,1.020) / |grad|: 4.161 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s] * 2D-GD: iter: 231 / (a,b): (0.109,1.020) / |grad|: 4.161 / stop at: 0.010:  76%|███████▌  | 227/300 [00:04<00:01, 44.26it/s]* 2D-GD: iter: 231 / (a,b): (0.109,1.020) / |grad|: 4.161 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 232 / (a,b): (0.109,1.020) / |grad|: 14.162 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 232 / (a,b): (0.109,1.020) / |grad|: 14.162 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 233 / (a,b): (0.109,1.020) / |grad|: 14.813 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 233 / (a,b): (0.109,1.020) / |grad|: 14.813 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 234 / (a,b): (0.109,1.020) / |grad|: 3.362 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s] * 2D-GD: iter: 234 / (a,b): (0.109,1.020) / |grad|: 3.362 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 235 / (a,b): (0.109,1.020) / |grad|: 11.369 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 235 / (a,b): (0.109,1.020) / |grad|: 11.369 / stop at: 0.010:  77%|███████▋  | 232/300 [00:04<00:01, 43.90it/s]* 2D-GD: iter: 236 / (a,b): (0.109,1.020) / |grad|: 6.547 / stop at: 0.010:  77%|███████▋  | 232/300 [00:05<00:01, 43.90it/s] * 2D-GD: iter: 236 / (a,b): (0.109,1.020) / |grad|: 6.547 / stop at: 0.010:  77%|███████▋  | 232/300 [00:05<00:01, 43.90it/s]* 2D-GD: iter: 236 / (a,b): (0.109,1.020) / |grad|: 6.547 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 237 / (a,b): (0.109,1.020) / |grad|: 4.434 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 237 / (a,b): (0.109,1.020) / |grad|: 4.434 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 238 / (a,b): (0.109,1.020) / |grad|: 4.172 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 238 / (a,b): (0.109,1.020) / |grad|: 4.172 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 239 / (a,b): (0.109,1.020) / |grad|: 12.872 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 239 / (a,b): (0.109,1.020) / |grad|: 12.872 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 240 / (a,b): (0.109,1.020) / |grad|: 6.686 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s] * 2D-GD: iter: 240 / (a,b): (0.109,1.020) / |grad|: 6.686 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 241 / (a,b): (0.109,1.020) / |grad|: 8.394 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 241 / (a,b): (0.109,1.020) / |grad|: 8.394 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 242 / (a,b): (0.109,1.020) / |grad|: 9.396 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 242 / (a,b): (0.109,1.020) / |grad|: 9.396 / stop at: 0.010:  79%|███████▉  | 237/300 [00:05<00:01, 43.53it/s]* 2D-GD: iter: 242 / (a,b): (0.109,1.020) / |grad|: 9.396 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 243 / (a,b): (0.109,1.020) / |grad|: 7.790 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 243 / (a,b): (0.109,1.020) / |grad|: 7.790 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 244 / (a,b): (0.109,1.020) / |grad|: 12.503 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 244 / (a,b): (0.109,1.020) / |grad|: 12.503 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 245 / (a,b): (0.109,1.020) / |grad|: 11.666 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 245 / (a,b): (0.109,1.020) / |grad|: 11.666 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 246 / (a,b): (0.109,1.020) / |grad|: 12.094 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 246 / (a,b): (0.109,1.020) / |grad|: 12.094 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 247 / (a,b): (0.109,1.020) / |grad|: 7.733 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s] * 2D-GD: iter: 247 / (a,b): (0.109,1.020) / |grad|: 7.733 / stop at: 0.010:  81%|████████  | 243/300 [00:05<00:01, 44.20it/s]* 2D-GD: iter: 247 / (a,b): (0.109,1.020) / |grad|: 7.733 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 248 / (a,b): (0.109,1.020) / |grad|: 7.359 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 248 / (a,b): (0.109,1.020) / |grad|: 7.359 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 249 / (a,b): (0.109,1.020) / |grad|: 12.428 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 249 / (a,b): (0.109,1.020) / |grad|: 12.428 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 250 / (a,b): (0.109,1.020) / |grad|: 6.410 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s] * 2D-GD: iter: 250 / (a,b): (0.109,1.020) / |grad|: 6.410 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 251 / (a,b): (0.109,1.020) / |grad|: 7.556 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 251 / (a,b): (0.109,1.020) / |grad|: 7.556 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 252 / (a,b): (0.109,1.020) / |grad|: 9.245 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 252 / (a,b): (0.109,1.020) / |grad|: 9.245 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 253 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 253 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  83%|████████▎ | 248/300 [00:05<00:01, 45.66it/s]* 2D-GD: iter: 253 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 254 / (a,b): (0.109,1.020) / |grad|: 12.504 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 254 / (a,b): (0.109,1.020) / |grad|: 12.504 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 255 / (a,b): (0.109,1.020) / |grad|: 7.931 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s] * 2D-GD: iter: 255 / (a,b): (0.109,1.020) / |grad|: 7.931 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 256 / (a,b): (0.109,1.020) / |grad|: 8.359 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 256 / (a,b): (0.109,1.020) / |grad|: 8.359 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 257 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 257 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 258 / (a,b): (0.109,1.020) / |grad|: 12.470 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 258 / (a,b): (0.109,1.020) / |grad|: 12.470 / stop at: 0.010:  85%|████████▍ | 254/300 [00:05<00:00, 47.30it/s]* 2D-GD: iter: 258 / (a,b): (0.109,1.020) / |grad|: 12.470 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 259 / (a,b): (0.109,1.020) / |grad|: 7.865 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s] * 2D-GD: iter: 259 / (a,b): (0.109,1.020) / |grad|: 7.865 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 260 / (a,b): (0.109,1.020) / |grad|: 8.680 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 260 / (a,b): (0.109,1.020) / |grad|: 8.680 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 261 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 261 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 262 / (a,b): (0.109,1.020) / |grad|: 7.359 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s] * 2D-GD: iter: 262 / (a,b): (0.109,1.020) / |grad|: 7.359 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 263 / (a,b): (0.109,1.020) / |grad|: 7.865 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 263 / (a,b): (0.109,1.020) / |grad|: 7.865 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 264 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 264 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  86%|████████▋ | 259/300 [00:05<00:00, 48.02it/s]* 2D-GD: iter: 264 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 265 / (a,b): (0.109,1.020) / |grad|: 8.601 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 265 / (a,b): (0.109,1.020) / |grad|: 8.601 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 266 / (a,b): (0.109,1.020) / |grad|: 12.127 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 266 / (a,b): (0.109,1.020) / |grad|: 12.127 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 267 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s] * 2D-GD: iter: 267 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 268 / (a,b): (0.109,1.020) / |grad|: 8.669 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 268 / (a,b): (0.109,1.020) / |grad|: 8.669 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 269 / (a,b): (0.109,1.020) / |grad|: 12.575 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 269 / (a,b): (0.109,1.020) / |grad|: 12.575 / stop at: 0.010:  88%|████████▊ | 265/300 [00:05<00:00, 49.14it/s]* 2D-GD: iter: 269 / (a,b): (0.109,1.020) / |grad|: 12.575 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 270 / (a,b): (0.109,1.020) / |grad|: 7.872 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s] * 2D-GD: iter: 270 / (a,b): (0.109,1.020) / |grad|: 7.872 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 271 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 271 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 272 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 272 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 273 / (a,b): (0.109,1.020) / |grad|: 7.862 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s] * 2D-GD: iter: 273 / (a,b): (0.109,1.020) / |grad|: 7.862 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 274 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 274 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  90%|█████████ | 270/300 [00:05<00:00, 47.27it/s]* 2D-GD: iter: 274 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 275 / (a,b): (0.109,1.020) / |grad|: 8.669 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 275 / (a,b): (0.109,1.020) / |grad|: 8.669 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 276 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 276 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 277 / (a,b): (0.109,1.020) / |grad|: 8.823 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s] * 2D-GD: iter: 277 / (a,b): (0.109,1.020) / |grad|: 8.823 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 278 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 278 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 279 / (a,b): (0.109,1.020) / |grad|: 8.669 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 279 / (a,b): (0.109,1.020) / |grad|: 8.669 / stop at: 0.010:  92%|█████████▏| 275/300 [00:05<00:00, 45.81it/s]* 2D-GD: iter: 279 / (a,b): (0.109,1.020) / |grad|: 8.669 / stop at: 0.010:  93%|█████████▎| 280/300 [00:05<00:00, 44.98it/s]* 2D-GD: iter: 280 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  93%|█████████▎| 280/300 [00:05<00:00, 44.98it/s]* 2D-GD: iter: 280 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  93%|█████████▎| 280/300 [00:05<00:00, 44.98it/s]* 2D-GD: iter: 281 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  93%|█████████▎| 280/300 [00:05<00:00, 44.98it/s] * 2D-GD: iter: 281 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  93%|█████████▎| 280/300 [00:05<00:00, 44.98it/s]* 2D-GD: iter: 282 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  93%|█████████▎| 280/300 [00:05<00:00, 44.98it/s]* 2D-GD: iter: 282 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  93%|█████████▎| 280/300 [00:05<00:00, 44.98it/s]* 2D-GD: iter: 283 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  93%|█████████▎| 280/300 [00:06<00:00, 44.98it/s]* 2D-GD: iter: 283 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  93%|█████████▎| 280/300 [00:06<00:00, 44.98it/s]* 2D-GD: iter: 284 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  93%|█████████▎| 280/300 [00:06<00:00, 44.98it/s]* 2D-GD: iter: 284 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  93%|█████████▎| 280/300 [00:06<00:00, 44.98it/s]* 2D-GD: iter: 284 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 285 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s] * 2D-GD: iter: 285 / (a,b): (0.109,1.020) / |grad|: 8.923 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 286 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 286 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 287 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 287 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 288 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 288 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 289 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s] * 2D-GD: iter: 289 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  95%|█████████▌| 285/300 [00:06<00:00, 44.31it/s]* 2D-GD: iter: 289 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 290 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 290 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 291 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 291 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 292 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 292 / (a,b): (0.109,1.020) / |grad|: 12.585 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 293 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s] * 2D-GD: iter: 293 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 294 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 294 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 295 / (a,b): (0.109,1.020) / |grad|: 8.630 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 295 / (a,b): (0.109,1.020) / |grad|: 8.630 / stop at: 0.010:  97%|█████████▋| 290/300 [00:06<00:00, 43.94it/s]* 2D-GD: iter: 295 / (a,b): (0.109,1.020) / |grad|: 8.630 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 296 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 296 / (a,b): (0.109,1.020) / |grad|: 8.629 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 297 / (a,b): (0.109,1.020) / |grad|: 12.648 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 297 / (a,b): (0.109,1.020) / |grad|: 12.648 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 298 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s] * 2D-GD: iter: 298 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 299 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 299 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010:  99%|█████████▊| 296/300 [00:06<00:00, 47.72it/s]* 2D-GD: iter: 299 / (a,b): (0.109,1.020) / |grad|: 8.602 / stop at: 0.010: 100%|██████████| 300/300 [00:06<00:00, 47.37it/s]

Now, let’s compare it to the previous example.

# MixCOBRA with default parameter
print("Estimated (alpha, beta) = ({}, {})".format(gc3_fit.optimization_outputs['opt_alpha'], gc3_fit.optimization_outputs['opt_beta']))

Estimated (alpha, beta) = (0.10872969775761142, 1.0202912420053827)

Look at the learning surface using draw_learning_curve() method.

gc3_fit.draw_learning_curve()

We evaluate the performance of the method on the testing data using MSE and MAPE.

from sklearn.metrics import mean_absolute_percentage_error
y_pred3 = gc3_fit.predict(X_test1)
print(mean_absolute_percentage_error(y_test1, y_pred3))
print(mean_squared_error(y_test1, y_pred3))

0.18056444737200344
146.90990212692168

Let’s look at qq-plot using draw_learning_curve() method.

gc3_fit.draw_learning_curve(y_test=y_test1, fig_type='qq')

Real dataset

We look at the California housing dataset from sklearn.datasets module. To illustrate the idea, we only work with the first \(1000\) observations.

from sklearn.datasets import fetch_california_housing
data = fetch_california_housing()
X_real, y_real = data['data'], data['target']

X_train_real, X_test_real, y_train_real, y_test_real = train_test_split(X_real[:1000,:], y_real[:1000], test_size=0.2)
print('shape: x_train = {} , x_train = {} , y_train = {} , y_test = {}'.format(X_train_real.shape, X_test_real.shape, y_train_real.shape, y_test_real.shape))

shape: x_train = (800, 8) , x_train = (200, 8) , y_train = (800,) , y_test = (200,)

We gave some random parameters to the method as follows.

gc_real = MixCOBRARegressor(opt_method="grid",
                            estimator_list=['random_forest', 
                                            'knn', 
                                            'ridge', 
                                            'lasso'],
                            estimator_params={
                                'random_forest' : {'n_estimators': 300},
                                'knn' : {'n_neighbors' : 5}})
gc_real_fit = gc_real.fit(X_train_real, y_train_real)

* 2D-grid search:   0%|          | 0/50 [00:00<?, ?it/s]* 2D-grid search:   2%|▏         | 1/50 [00:00<00:16,  3.00it/s]* 2D-grid search:   4%|▍         | 2/50 [00:00<00:15,  3.00it/s]* 2D-grid search:   6%|▌         | 3/50 [00:01<00:17,  2.75it/s]* 2D-grid search:   8%|▊         | 4/50 [00:01<00:16,  2.74it/s]* 2D-grid search:  10%|█         | 5/50 [00:01<00:15,  2.83it/s]* 2D-grid search:  12%|█▏        | 6/50 [00:02<00:15,  2.84it/s]* 2D-grid search:  14%|█▍        | 7/50 [00:02<00:14,  2.88it/s]* 2D-grid search:  16%|█▌        | 8/50 [00:02<00:14,  2.88it/s]* 2D-grid search:  18%|█▊        | 9/50 [00:03<00:14,  2.75it/s]* 2D-grid search:  20%|██        | 10/50 [00:03<00:14,  2.78it/s]* 2D-grid search:  22%|██▏       | 11/50 [00:03<00:13,  2.84it/s]* 2D-grid search:  24%|██▍       | 12/50 [00:04<00:13,  2.85it/s]* 2D-grid search:  26%|██▌       | 13/50 [00:04<00:12,  2.85it/s]* 2D-grid search:  28%|██▊       | 14/50 [00:04<00:12,  2.80it/s]* 2D-grid search:  30%|███       | 15/50 [00:05<00:12,  2.75it/s]* 2D-grid search:  32%|███▏      | 16/50 [00:05<00:12,  2.82it/s]* 2D-grid search:  34%|███▍      | 17/50 [00:05<00:11,  2.96it/s]* 2D-grid search:  36%|███▌      | 18/50 [00:06<00:10,  3.06it/s]* 2D-grid search:  38%|███▊      | 19/50 [00:06<00:10,  3.04it/s]* 2D-grid search:  40%|████      | 20/50 [00:06<00:10,  2.94it/s]* 2D-grid search:  42%|████▏     | 21/50 [00:07<00:10,  2.72it/s]* 2D-grid search:  44%|████▍     | 22/50 [00:07<00:10,  2.65it/s]* 2D-grid search:  46%|████▌     | 23/50 [00:08<00:09,  2.71it/s]* 2D-grid search:  48%|████▊     | 24/50 [00:08<00:09,  2.83it/s]* 2D-grid search:  50%|█████     | 25/50 [00:08<00:08,  2.83it/s]* 2D-grid search:  52%|█████▏    | 26/50 [00:09<00:08,  2.69it/s]* 2D-grid search:  54%|█████▍    | 27/50 [00:09<00:08,  2.63it/s]* 2D-grid search:  56%|█████▌    | 28/50 [00:09<00:08,  2.73it/s]* 2D-grid search:  58%|█████▊    | 29/50 [00:10<00:07,  2.77it/s]* 2D-grid search:  60%|██████    | 30/50 [00:10<00:07,  2.72it/s]* 2D-grid search:  62%|██████▏   | 31/50 [00:11<00:07,  2.68it/s]* 2D-grid search:  64%|██████▍   | 32/50 [00:11<00:06,  2.66it/s]* 2D-grid search:  66%|██████▌   | 33/50 [00:11<00:06,  2.72it/s]* 2D-grid search:  68%|██████▊   | 34/50 [00:12<00:05,  2.84it/s]* 2D-grid search:  70%|███████   | 35/50 [00:12<00:05,  2.97it/s]* 2D-grid search:  72%|███████▏  | 36/50 [00:12<00:04,  3.07it/s]* 2D-grid search:  74%|███████▍  | 37/50 [00:13<00:04,  3.00it/s]* 2D-grid search:  76%|███████▌  | 38/50 [00:13<00:04,  2.75it/s]* 2D-grid search:  78%|███████▊  | 39/50 [00:13<00:03,  2.82it/s]* 2D-grid search:  80%|████████  | 40/50 [00:14<00:03,  2.76it/s]* 2D-grid search:  82%|████████▏ | 41/50 [00:14<00:03,  2.75it/s]* 2D-grid search:  84%|████████▍ | 42/50 [00:14<00:02,  2.82it/s]* 2D-grid search:  86%|████████▌ | 43/50 [00:15<00:02,  2.75it/s]* 2D-grid search:  88%|████████▊ | 44/50 [00:15<00:02,  2.64it/s]* 2D-grid search:  90%|█████████ | 45/50 [00:16<00:01,  2.79it/s]* 2D-grid search:  92%|█████████▏| 46/50 [00:16<00:01,  2.73it/s]* 2D-grid search:  94%|█████████▍| 47/50 [00:16<00:01,  2.87it/s]* 2D-grid search:  96%|█████████▌| 48/50 [00:17<00:00,  2.95it/s]* 2D-grid search:  98%|█████████▊| 49/50 [00:17<00:00,  2.78it/s]* 2D-grid search: 100%|██████████| 50/50 [00:17<00:00,  2.71it/s]* 2D-grid search: 100%|██████████| 50/50 [00:17<00:00,  2.80it/s]

Now, let’s look at the obtained bandwidth and the optimization result.

# MixCOBRA with default parameter
print("Estimated (alpha, beta) = ({}, {})".format(gc_real_fit.optimization_outputs['opt_alpha'], gc_real_fit.optimization_outputs['opt_beta']))

Estimated (alpha, beta) = (1e-05, 0.40817285714285717)

We look at the numerical and graphical performance.

y_pred_real = gc_real_fit.predict(X_test_real)
print(mean_absolute_percentage_error(y_test_real, y_pred_real))
print(mean_squared_error(y_test_real, y_pred_real))
gc_real_fit.draw_learning_curve(y_test=y_test_real, fig_type='qq')

0.17461897730576703
0.20723550267745572

Compare `MixCOBRARegressor` to Adaboost

We campare the fitted method on California data with Adaboost method.

from sklearn.ensemble import AdaBoostRegressor

ada = AdaBoostRegressor(n_estimators=1000)
ada_fit = ada.fit(X_train_real, y_train_real)
ada_pred = ada_fit.predict(X_test_real)
print(mean_absolute_percentage_error(y_test_real, ada_pred))
print(mean_squared_error(y_test_real, ada_pred))

0.24756894646736627
0.26865811086268854

Pretrained basic estimators

You can also train other models then aggregate them using our method. Here, we build pretrained estimators including XGBoost then aggregate it to some sklearn basic estimators in MixCOBRARegressor.

We first split the training data into two parts: \(X_k\) for building basic estimators, and \(X_\ell\) for aggregation. We use the constructed estimators to predict the test data and both the input \(X_{\text{test}}\) and its predictions pred_feature_test are used in the final predictions.

import numpy as np
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor

# X_k and X_l split
id_k = np.random.permutation(range(len(y_train_real)))
k =int(.5 * len(y_train_real))
X_k, X_l, y_k, y_l = X_train_real[id_k[:k],:], X_train_real[id_k[k:],:], y_train_real[id_k[:k]], y_train_real[id_k[k:]]

# Building basic estiators
rf_real = RandomForestRegressor(n_estimators=300).fit(X_k, y_k)
lm_real = LinearRegression().fit(X_k, y_k)
knn_real = KNeighborsRegressor(n_neighbors=10).fit(X_k, y_k)
tr_real = DecisionTreeRegressor(min_samples_leaf=5).fit(X_k, y_k)

# External XGBoost estiator
import xgboost 
xgb = xgboost.XGBRegressor(n_estimators = 500)
xgb_real = xgb.fit(X_k, y_k)

# All pretrained estimators
basic_estimators = (rf_real, lm_real, knn_real, tr_real, xgb_real)

# Predicted features on X_l for aggregation
pred_feature_l = np.column_stack([est.predict(X_l) for est in basic_estimators])

# Predicted features on Testing data
pred_feature_test = np.column_stack([est.predict(X_test_real) for est in basic_estimators])

To fit the aggregation method on predicted features, we need to provide both input and predicted features to fit method.

gc4_fit = MixCOBRARegressor(opt_method='grid').fit(X=X_l,
                                                   Pred_features=pred_feature_l,
                                                   y=y_l)

* 2D-grid search:   0%|          | 0/50 [00:00<?, ?it/s]* 2D-grid search:   2%|▏         | 1/50 [00:00<00:19,  2.52it/s]* 2D-grid search:   4%|▍         | 2/50 [00:00<00:19,  2.50it/s]* 2D-grid search:   6%|▌         | 3/50 [00:01<00:17,  2.65it/s]* 2D-grid search:   8%|▊         | 4/50 [00:01<00:16,  2.73it/s]* 2D-grid search:  10%|█         | 5/50 [00:01<00:15,  2.82it/s]* 2D-grid search:  12%|█▏        | 6/50 [00:02<00:15,  2.88it/s]* 2D-grid search:  14%|█▍        | 7/50 [00:02<00:15,  2.78it/s]* 2D-grid search:  16%|█▌        | 8/50 [00:02<00:15,  2.73it/s]* 2D-grid search:  18%|█▊        | 9/50 [00:03<00:14,  2.85it/s]* 2D-grid search:  20%|██        | 10/50 [00:03<00:13,  3.03it/s]* 2D-grid search:  22%|██▏       | 11/50 [00:03<00:12,  3.05it/s]* 2D-grid search:  24%|██▍       | 12/50 [00:04<00:12,  3.10it/s]* 2D-grid search:  26%|██▌       | 13/50 [00:04<00:12,  2.85it/s]* 2D-grid search:  28%|██▊       | 14/50 [00:04<00:13,  2.73it/s]* 2D-grid search:  30%|███       | 15/50 [00:05<00:12,  2.77it/s]* 2D-grid search:  32%|███▏      | 16/50 [00:05<00:12,  2.80it/s]* 2D-grid search:  34%|███▍      | 17/50 [00:06<00:11,  2.86it/s]* 2D-grid search:  36%|███▌      | 18/50 [00:06<00:10,  3.07it/s]* 2D-grid search:  38%|███▊      | 19/50 [00:06<00:10,  2.92it/s]* 2D-grid search:  40%|████      | 20/50 [00:07<00:10,  2.74it/s]* 2D-grid search:  42%|████▏     | 21/50 [00:07<00:10,  2.85it/s]* 2D-grid search:  44%|████▍     | 22/50 [00:07<00:09,  2.85it/s]* 2D-grid search:  46%|████▌     | 23/50 [00:08<00:09,  2.82it/s]* 2D-grid search:  48%|████▊     | 24/50 [00:08<00:09,  2.75it/s]* 2D-grid search:  50%|█████     | 25/50 [00:08<00:09,  2.71it/s]* 2D-grid search:  52%|█████▏    | 26/50 [00:09<00:08,  2.75it/s]* 2D-grid search:  54%|█████▍    | 27/50 [00:09<00:08,  2.86it/s]* 2D-grid search:  56%|█████▌    | 28/50 [00:09<00:07,  2.98it/s]* 2D-grid search:  58%|█████▊    | 29/50 [00:10<00:06,  3.04it/s]* 2D-grid search:  60%|██████    | 30/50 [00:10<00:06,  2.98it/s]* 2D-grid search:  62%|██████▏   | 31/50 [00:10<00:06,  2.82it/s]* 2D-grid search:  64%|██████▍   | 32/50 [00:11<00:06,  2.75it/s]* 2D-grid search:  66%|██████▌   | 33/50 [00:11<00:06,  2.71it/s]* 2D-grid search:  68%|██████▊   | 34/50 [00:12<00:05,  2.79it/s]* 2D-grid search:  70%|███████   | 35/50 [00:12<00:05,  2.84it/s]* 2D-grid search:  72%|███████▏  | 36/50 [00:12<00:04,  2.81it/s]* 2D-grid search:  74%|███████▍  | 37/50 [00:13<00:04,  2.87it/s]* 2D-grid search:  76%|███████▌  | 38/50 [00:13<00:04,  2.94it/s]* 2D-grid search:  78%|███████▊  | 39/50 [00:13<00:03,  3.01it/s]* 2D-grid search:  80%|████████  | 40/50 [00:14<00:03,  3.01it/s]* 2D-grid search:  82%|████████▏ | 41/50 [00:14<00:03,  2.99it/s]* 2D-grid search:  84%|████████▍ | 42/50 [00:14<00:02,  2.80it/s]* 2D-grid search:  86%|████████▌ | 43/50 [00:15<00:02,  2.74it/s]* 2D-grid search:  88%|████████▊ | 44/50 [00:15<00:02,  2.77it/s]* 2D-grid search:  90%|█████████ | 45/50 [00:15<00:01,  2.76it/s]* 2D-grid search:  92%|█████████▏| 46/50 [00:16<00:01,  2.87it/s]* 2D-grid search:  94%|█████████▍| 47/50 [00:16<00:01,  2.99it/s]* 2D-grid search:  96%|█████████▌| 48/50 [00:16<00:00,  2.90it/s]* 2D-grid search:  98%|█████████▊| 49/50 [00:17<00:00,  2.81it/s]* 2D-grid search: 100%|██████████| 50/50 [00:17<00:00,  2.79it/s]* 2D-grid search: 100%|██████████| 50/50 [00:17<00:00,  2.84it/s]

We look at the optimization algorithm performance.

# MixCOBRA with default parameter
print("Estimated (alpha, beta) = ({}, {})".format(gc4_fit.optimization_outputs['opt_alpha'], gc4_fit.optimization_outputs['opt_beta']))

Estimated (alpha, beta) = (1e-05, 0.40817285714285717)

Now, let’s look at the result.

gc4_fit.draw_learning_curve()
pred_add = gc4_fit.predict(X = X_test_real, 
                           Pred_X = pred_feature_test)
print(mean_absolute_percentage_error(y_test_real, pred_add))
print(mean_squared_error(y_test_real, pred_add))

0.17912814880819775
0.2050303630331598

GradientCobra Python Library

Introduction to MixCOBRA method

MixCOBRARegressor method

Parameters

Returns:

Methods:

Installation of the library from `pypi`

Importing some packages

Simulated data

\(\bullet\) `MixCOBRARegressor` with default parameters

\(\bullet\) Use one bandwidth parameter instead of (\(\alpha, \beta\))

\(\bullet\) `MixCOBRARegressor` with non-default parameters

Real dataset

Compare `MixCOBRARegressor` to Adaboost

Pretrained basic estimators

References

Read also:

Introduction to MixCOBRA method

MixCOBRARegressor method

Parameters

Returns:

Methods:

Installation of the library from pypi

Importing some packages

Simulated data

\(\bullet\) MixCOBRARegressor with default parameters

\(\bullet\) Use one bandwidth parameter instead of (\(\alpha, \beta\))

\(\bullet\) MixCOBRARegressor with non-default parameters

Real dataset

Compare MixCOBRARegressor to Adaboost

Pretrained basic estimators

References

Read also:

Installation of the library from `pypi`

\(\bullet\) `MixCOBRARegressor` with default parameters

\(\bullet\) `MixCOBRARegressor` with non-default parameters

Compare `MixCOBRARegressor` to Adaboost