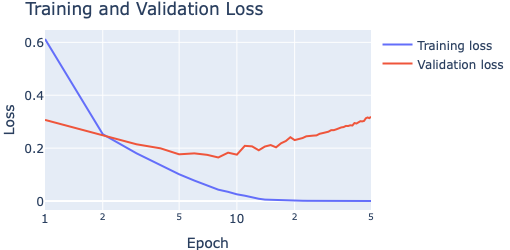
# Training the network
history = model.fit(
X_train[:10000,:], train_labels[:10000],
epochs=50, batch_size=64, verbose=0,
validation_split=0.1)
# evaluation
loss, accuracy = model.evaluate(
X_test, test_labels, verbose=0)
# Extract loss values
train_loss = history.history['loss']
val_loss = history.history['val_loss']
# Plot the learning curves
epochs = list(range(1, len(train_loss) + 1))
fig1 = go.Figure(go.Scatter(
x=epochs, y=train_loss, name="Training loss"))
fig1.add_trace(
go.Scatter(x=epochs, y=val_loss,
name="Training loss"))
fig1.update_layout(
title="Training and Validation Loss",
width=510, height=250,
xaxis=dict(title="Epoch", type="log"),
yaxis=dict(title="Loss"))
fig1.show()
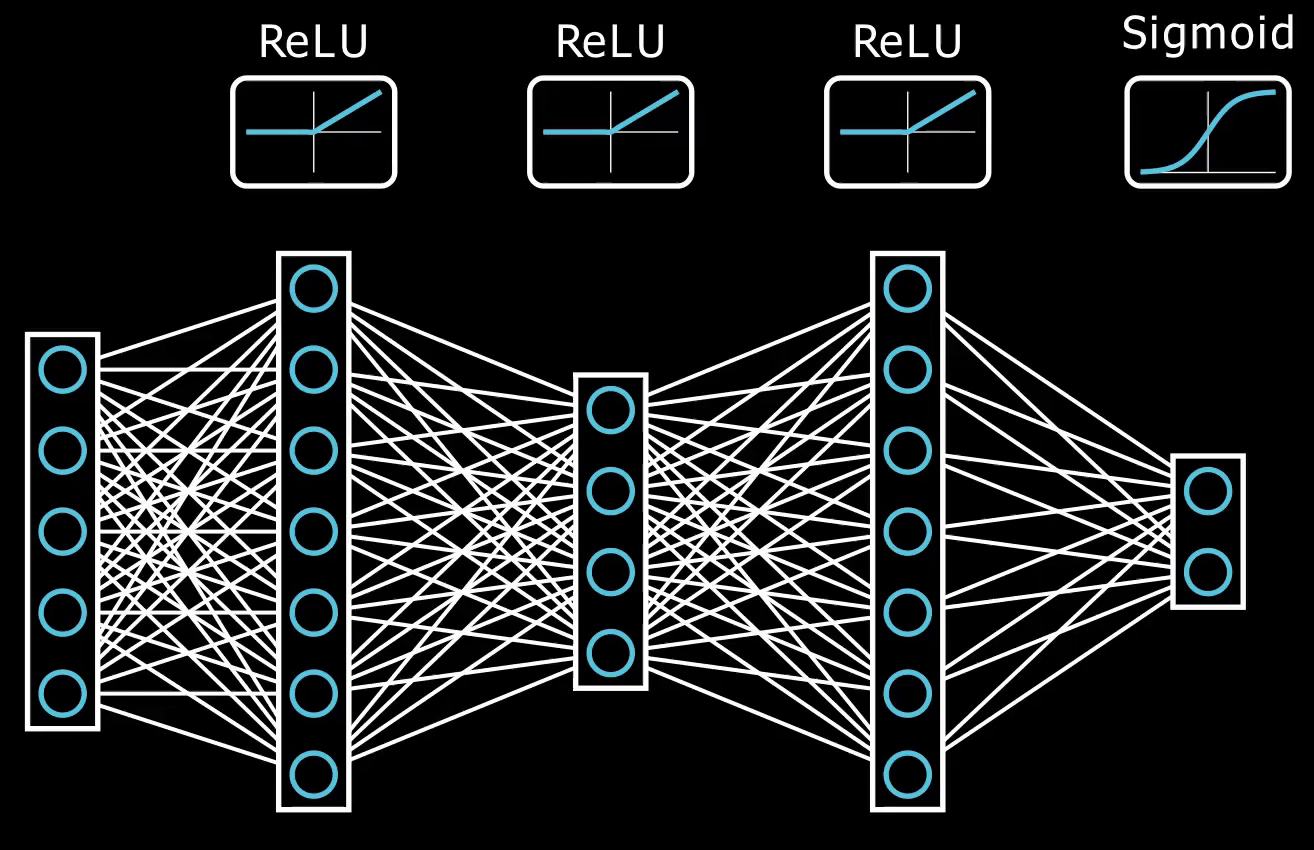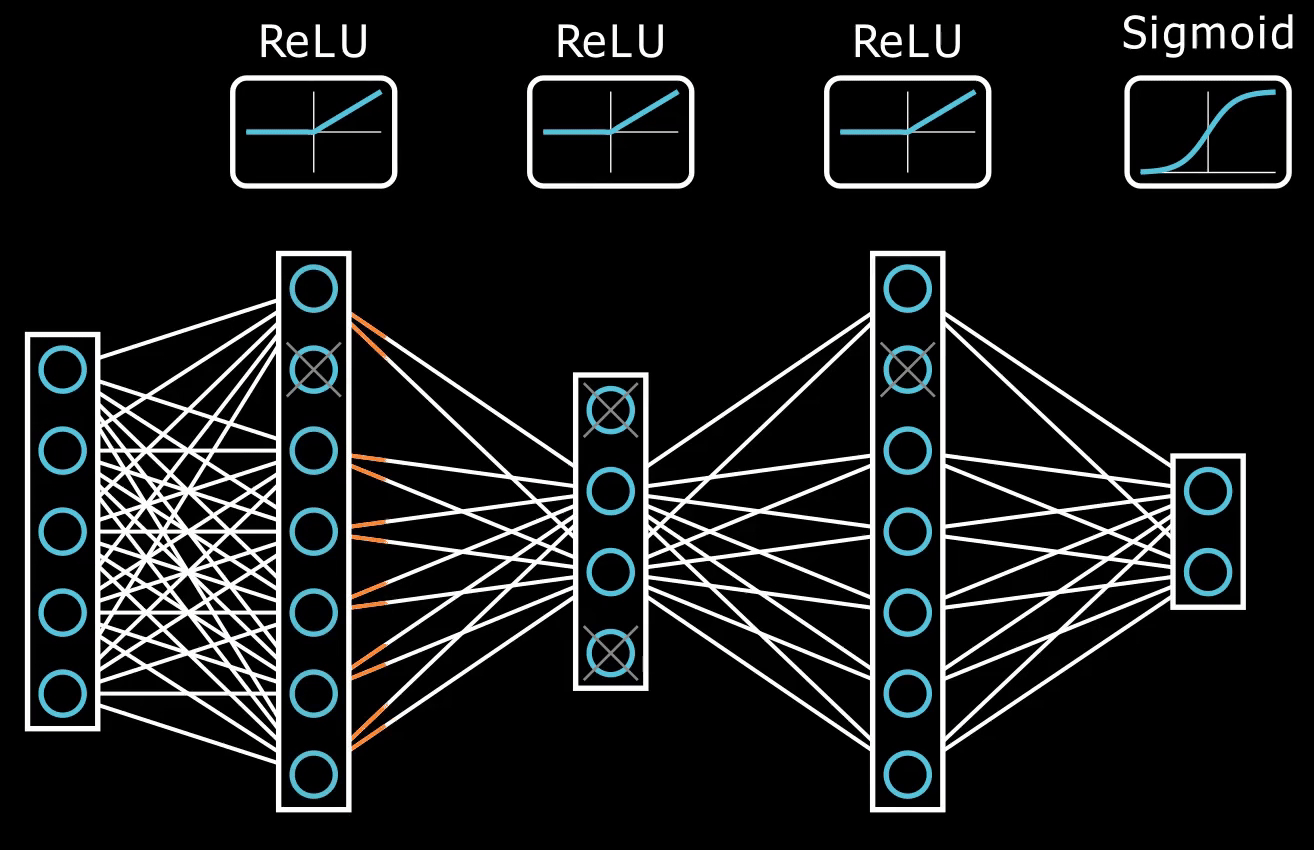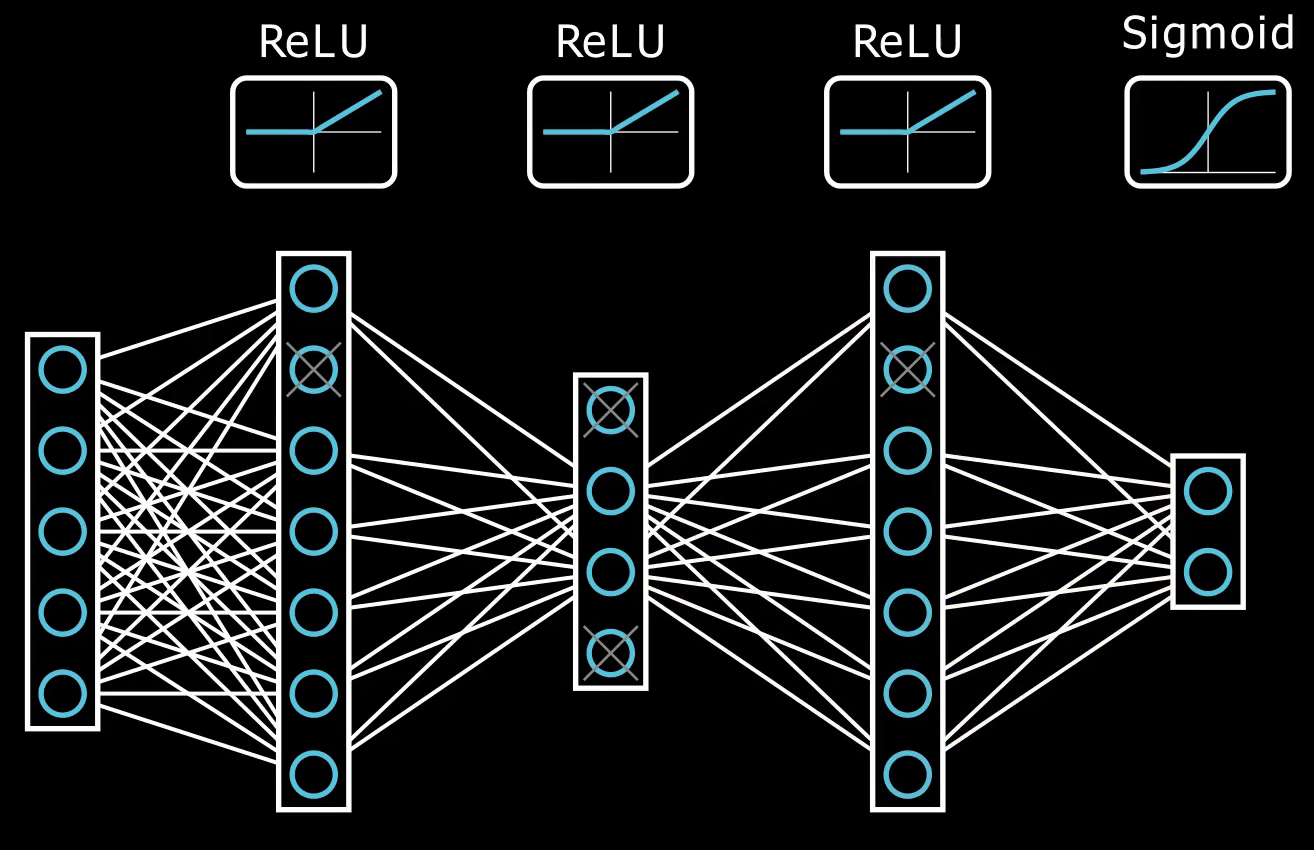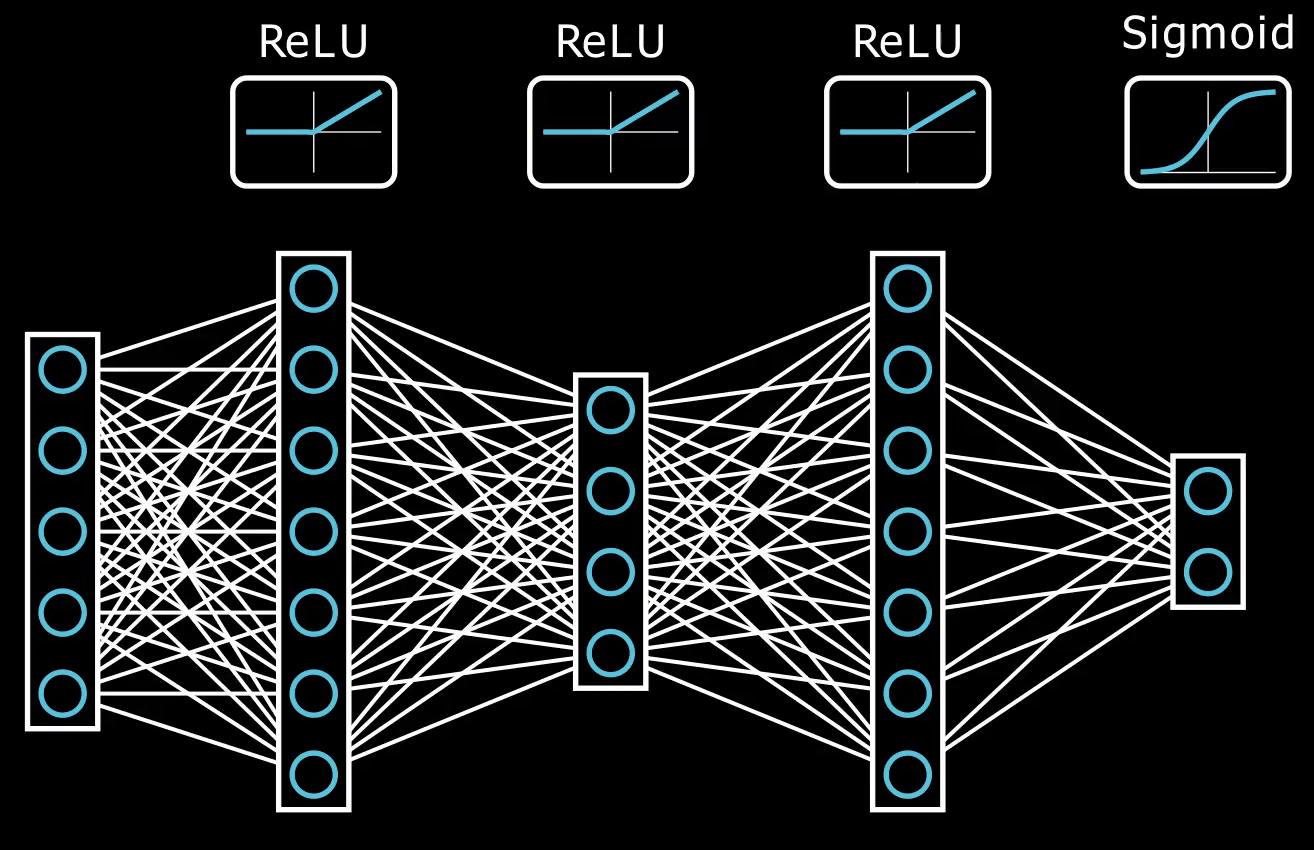
 Deep Neural Network
Deep Neural Network