| x1 | x2 | y |
|---|---|---|
| -0.752759 | 2.704286 | 1 |
| 1.935603 | -0.838856 | 0 |
Advanced Machine Learning
Code:
AMSI61AML
3. Logistic Regression & Regularization
Binary Logistic Regression
Objective: classify whether \(y=0\) or \(1\) using its input \(\text{x}\in\mathbb{R}^d\).
Classifying \(\Leftrightarrow\) identifying the
decision boundary.A good decision boundary should separates classes well.
Normally:
- Far from it = more certain.
- Close to it = less certain.
- Assumption: The decision boundary is
linear.
Code
import plotly.express as px
import plotly.graph_objects as go
fig = px.scatter(
data_toy1, x="x1", y="x2",
color="y")
# Lines
line_coefs = np.array(
[[1, 1, -2], [-1, 0.3, 0.5], [-0.5, 0.3, -1], [0.1, -1, 1]])
frames = []
x_line = np.array([np.min(x1[:,1]), np.max(x1[:,1])])
y_range = np.array([np.min(x1[:,2]), np.max(x1[:,2])])
id_small = np.argsort(np.abs(x1[:,1]) + np.abs(x1[:,2]))[5]
point_far = np.array([x_line[0], y_range[1]])
point_near = np.array([x1[id_small,1],x1[id_small,2]])
for i, coef in enumerate(line_coefs):
y_line = (-coef[0] - coef[1] * x_line) / coef[2]
a, b = -coef[1]/coef[2], -coef[0]/coef[2]
point_proj_far = np.array([(point_far[0]+a*point_far[1]-a*b)/(a**2+1), a*(point_far[0]+a*point_far[1]-a*b)/(a**2+1)+b])
point_proj_near = np.array([(point_near[0]+a*point_near[1]-a*b)/(a**2+1), a*(point_near[0]+a*point_near[1]-a*b)/(a**2+1)+b])
p1 = np.row_stack([point_far, point_proj_far])
p2 = np.row_stack([point_near, point_proj_near])
frames.append(go.Frame(
data=[fig.data[0],
fig.data[1],
go.Scatter(
x=p1[:,0],
y=p1[:,1],
name="Far from boundary",
line=dict(dash="dash"),
visible="legendonly"
),
go.Scatter(
x=p2[:,0],
y=p2[:,1],
name="Close to boundary",
line=dict(dash="dash"),
visible="legendonly"
),
go.Scatter(
x=x_line, y=y_line, mode='lines',
line=dict(width=3, color="black"),
name=f'Line: {i+1}')],
name=f'{i+1}'))
y_line = (-line_coefs[0,0] - line_coefs[0,1] * x_line) / line_coefs[0,2]
a, b = -line_coefs[0,0]/line_coefs[0,2], - line_coefs[0,1]/line_coefs[0,2]
point_proj_far = np.array([(point_far[0]+a*point_far[1]-a*b)/(a**2+1), a*(point_far[0]+a*point_far[1]-a*b)/(a**2+1)+b])
point_proj_near = np.array([(point_near[0]+a*point_near[1]-a*b)/(a**2+1), a*(point_near[0]+a*point_near[1]-a*b)/(a**2+1)+b])
p1 = np.row_stack([point_far, point_proj_far])
p2 = np.row_stack([point_near, point_proj_near])
fig1 = go.Figure(
data=[
fig.data[0],
fig.data[1],
go.Scatter(
x=p1[:,0],
y=p1[:,1],
name="Far from boundary",
line=dict(dash="dash"),
visible="legendonly"
),
go.Scatter(
x=p2[:,0],
y=p2[:,1],
name="Close to boundary",
line=dict(dash="dash"),
visible="legendonly"
),
go.Scatter(
x=x_line, y=y_line, mode='lines',
line=dict(width=3, color="black"),
name=f'Line: 1')
],
layout=go.Layout(
title="1st simulated data & boundary lines",
xaxis=dict(title="x1", range=[-3.4, 3.4]),
yaxis=dict(title="x2", range=[-3.4, 3.4]),
updatemenus=[{
"buttons": [
{
"args": [None, {"frame": {"duration": 1000, "redraw": True}, "fromcurrent": True, "mode": "immediate"}],
"label": "Play",
"method": "animate"
},
{
"args": [[None], {"frame": {"duration": 0, "redraw": False}, "mode": "immediate"}],
"label": "Stop",
"method": "animate"
}
],
"type": "buttons",
"showactive": False,
"x": -0.1,
"y": 1.25,
"pad": {"r": 10, "t": 50}
}],
sliders=[{
"active": 0,
"currentvalue": {"prefix": "Line: "},
"pad": {"t": 50},
"steps": [{"label": f"{i}",
"method": "animate",
"args": [[f'{i}'], {"frame": {"duration": 1000, "redraw": True}, "mode": "immediate",
"transition": {"duration": 10}}]}
for i in range(1,5)]
}]
),
frames=frames
)
fig1.update_layout(height=370, width=500)
fig1.show()Binary Logistic Regression
Model intuition
- If \((P):\beta_0+\sum_{j=1}^d\beta_jx_j=0\) is a boundary (hyperplane) with some orthogonal vector \(\vec{\beta}\in\mathbb{R}^d\), then for any input \(\text{x}_0\in\mathbb{R}^d:\) \[\color{green}{z_0}=\color{green}{\beta_0+\text{x}_0^T\vec{\beta}}\ \text{is the relative distance from }\text{x}_0\to (P).\]
- That’s to say that
- \(\color{green}{z_0}>0\Leftrightarrow \text{x}_0\) is above the boundary \((P)\).
- \(|\color{green}{z_0}|\) is large \(\Leftrightarrow\) \(\text{x}_0\) is far from \((P)\).
- \((P)\) is a good boundary:
- \(|\color{green}{z_0}|\) large \(\Rightarrow\) “certain about its class”.
- \(|\color{green}{z_0}|\) small \(\Rightarrow\) “less certain about its class”.
Binary Logistic Regression
Model intuition
- \((P)\) is a good boundary:
- \(|\color{green}{z_0}|\) large \(\Rightarrow\) “certain about its class”.
- \(|\color{green}{z_0}|\) small \(\Rightarrow\) “less certain about its class”.
- Sigmoid function, \(\sigma:\mathbb{R}\to (0,1)\)
\[\color{green}{z}\mapsto\sigma(\color{green}{z})=\frac{1}{1+\exp(-\color{green}{z})}.\]
Key ideas
- \(\color{green}{z_0}=\color{green}{\beta_0+\text{x}_0^T\vec{\beta}}\) is the relative distance of \(\text{x}_0\) w.r.t \((P)\).
- Sigmoid can converts this relative distance into probability.
Binary Logistic Regression
Model
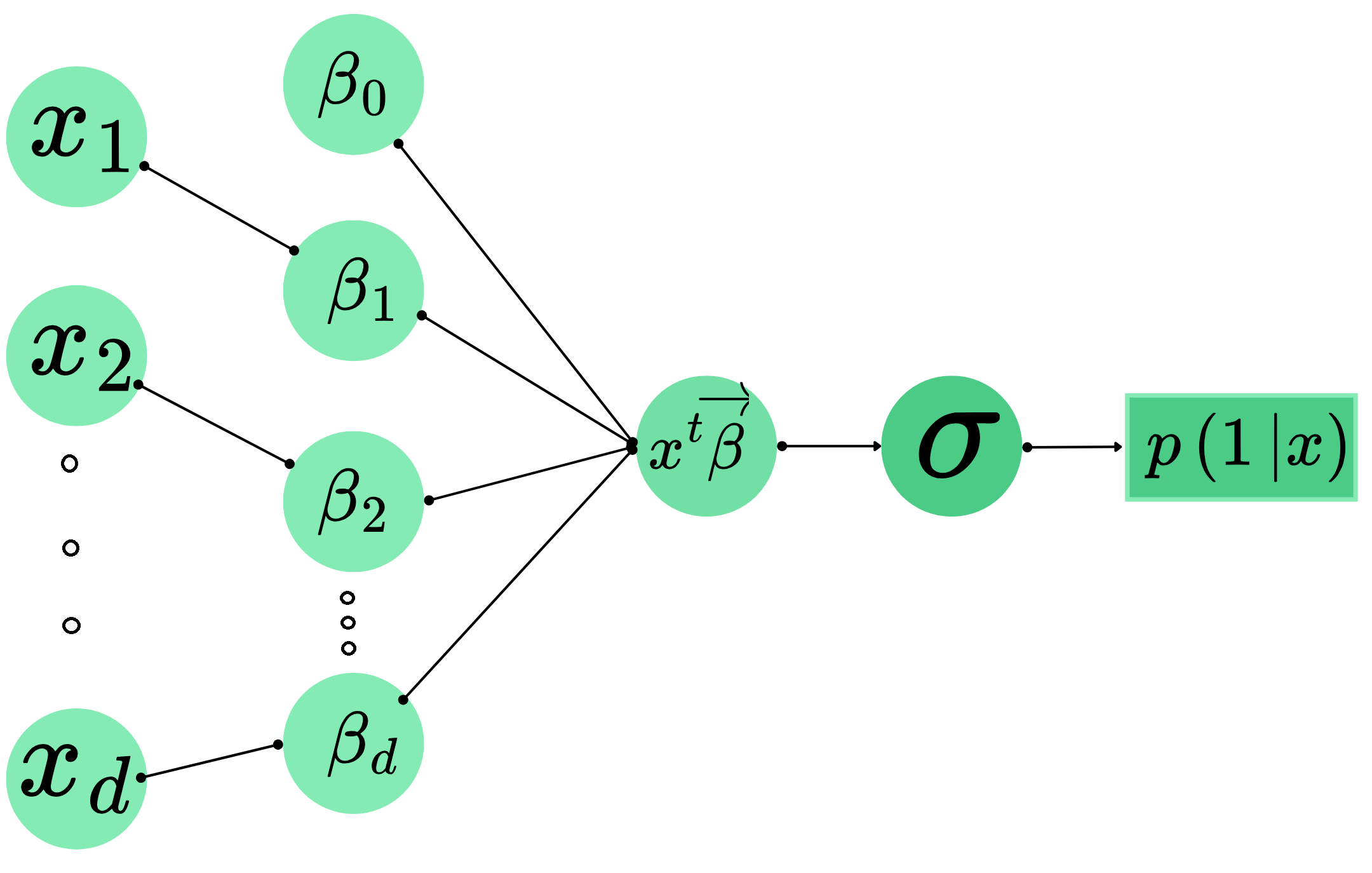
- For any parameters \(\beta_0\in\mathbb{R},\vec{\beta}=(\beta_1,\dots, \beta_d)\in\mathbb{R}^d\), we assume for any input data \(\text{x}\in\mathbb{R}^d\) that the probability that \(\text{x}\) belongs to class \(1\) is given by
\[\begin{align*} \mathbb{P}(Y=1|X=\text{x})=\sigma(\beta_0+\text{x}^T\vec{\beta})=\frac{1}{1+\exp(-\beta_0-\text{x}^T\vec{\beta})}:=p(1|\text{x})=1-p(0|\text{x}). \end{align*}\]
- Interpretation:
- \(\text{x}\) has relative distance \(z=\beta_0+\text{x}^T\vec{\beta}\) to the boundary defined by \(\beta_0\in\mathbb{R}\) and \(\vec{\beta}\in\mathbb{R}^d\).
- This relative distance is converted to probability using sigmoid function: \(\sigma(z)\).
- If \(z>>0\), then \(\text{x}\) is far above the boundary, and it is highly likely to be in class \(1\).
- If \(z<<0\), then \(\text{x}\) is far below the boundary, and it is highly likely to be in class \(0\).
- If \(z\approx 0\), \(\text{x}\) is close to the boundary, and its class is uncertain!
- The relative distance is known as
log-odd:\[\text{Logit}(p(1|\text{x}_i))=\log\Big(\frac{p(1|\text{x})}{p(0|\text{x})}\Big)=\beta_0+\sum_{j=1}\beta_jx_{ij}.\]
Binary Logistic Regression
Example: 1st Simulated Data
- If \((\beta_0,\beta_1,\beta_2)=(1, 1, -2)\), compute \(p(1|\text{x})\) of the following data:
| x1 | x2 | y |
|---|---|---|
| 2.489186 | -0.779048 | 0 |
| -2.572868 | -1.086146 | 1 |
| 2.767143 | 2.432104 | 0 |
Compute relative distance \(z_i=\beta_0+\text{x}_i^T\vec{\beta}\), then \(p(1|\text{x}_i)\) \[\begin{align*}z_1&=1+1(2.489186)-2(-0.779048)\\ &=5.047282>0\\ \Rightarrow p(1|\text{x}_1)&=\sigma(z_1)=1/(1+e^{-5.047282})=\color{blue}{0.9936}.\\ \\ z_2&=1+1(-2.572868)-2(-1.086146)\\ &=0.599424>0\\ \Rightarrow p(1|\text{x}_2)&=\sigma(z_2)=1/(1+e^{-0.599424})=\color{blue}{0.6455}.\\ \\ z_2&=1+1(2.767143)-2(2.432104)\\ &=-1.097065 < 0\\ \Rightarrow p(1|\text{x}_3)&=\sigma(z_3)=1/(1+e^{-(-1.097065)})=\color{red}{0.2503}.\end{align*}\]
Interpretation: \(\text{x}_1,\text{x}_2\) are located above the line \((P):1+x_1-2x_2\) and are predicted to be in class \(\color{blue}{1}\). On the other hand, \(\text{x}_3\) is located below the line and is predicted to be in class \(\color{red}{0}\).
Next, we shall discuss how to define a criterion to obtain the optimal parameters \(\color{green}{\widehat{\beta_0}}\) and \(\color{green}{\widehat{\vec{\beta}}}\).
Binary Logistic Regression
Conditional likelihood
Data: \({\cal D}=\{(\text{x}_1,y_1),...,(\text{x}_n,y_n)\}\subset\mathbb{R}^d\times \{0,1\}\).
Objective: search for \(\beta_0\in\mathbb{R},\vec{\beta}\in\mathbb{R}^d\) such that the
modelis best aligned with the data \({\cal D}\): \[p(y_i|\text{x}_i)\text{ is large for all }i\in\{1,\dots,n\}.\]Conditional Likelihood Function: If the data are
iid, one has \[\begin{align*}{L}(\beta_0,\vec{\beta})&=\mathbb{P}(Y_1=y_1,\dots,Y_n=y_n|X_1=\text{x}_1,\dots,X_n=\text{x}_n)\\ &=\prod_{i=1}^np(y_i|\text{x}_i)\\ &=\prod_{i=1}^n\Big[p(1|\text{x}_i)\Big]^{y_i}\Big[p(0|\text{x}_i)\Big]^{1-y_i}\\ &=\prod_{i=1}^n\Big[\sigma(\beta_0+\text{x}_i^T\vec{\beta})\Big]^{y_i}\Big[(1-\sigma(\beta_0+\text{x}_i^T\vec{\beta}))\Big]^{1-y_i}. \end{align*}\]
Binary Logistic Regression
Log Loss/Logistic Loss/Cross-entropy
- Log-Conditional Likelihood function: recall that \(p(1|\text{x}_i)=\sigma(\beta_0+\text{x}_i^T\vec{\beta})\) then \[\begin{align*}\log[L(\beta_0,\vec{\beta})]&=\sum_{i=1}^n\Big[y_i\log[p(1|\text{x}_i)]+(1-y_i)\log[p(0|\text{x}_i)]\Big].\qquad(1) \end{align*}\]
- Log-loss or logistic loss or Cross-entropy: \[\color{red}{{\cal L}(\beta_0,\vec{\beta})=-\log[L(\beta_0,\vec{\beta})]}.\]
- Objective: searching for \(\color{green}{\widehat{\beta}_0}\in\mathbb{R}\),\(\color{green}{\widehat{\vec{\beta}}}\in\mathbb{R}^d\) that minimizes \(\color{red}{{\cal L}(\beta_0,\vec{\beta})}\), i.e., \[{\cal L}(\color{green}{\widehat{\beta}_0,\widehat{\vec{\beta}}})=\inf_{\beta_0\in\mathbb{R},\vec{\beta}\in\mathbb{R}^d}\color{red}{{\cal L}(\beta_0,\vec{\beta})}.\]
- Ex: The 1st simulated data 👉
Binary Logistic Regression
Log Loss/Logistic Loss/Cross-entropy
- Log-Conditional Likelihood function: recall that \(p(1|\text{x}_i)=\sigma(\beta_0+\text{x}_i^T\vec{\beta})\) then \[\begin{align*}\log[L(\beta_0,\vec{\beta})]&=\sum_{i=1}^n\Big[y_i\log[p(1|\text{x}_i)]+(1-y_i)\log[p(0|\text{x}_i)]\Big]. \end{align*} \qquad(1)\]
- Log-loss or logistic loss or Cross-entropy: \[\color{red}{{\cal L}(\beta_0,\vec{\beta})=-\log[L(\beta_0,\vec{\beta})]}.\]
- Objective: searching for \(\color{green}{\widehat{\beta}_0}\in\mathbb{R}\),\(\color{green}{\widehat{\vec{\beta}}}\in\mathbb{R}^d\) that minimizes \(\color{red}{{\cal L}(\beta_0,\vec{\beta})}\), i.e., \[{\cal L}(\color{green}{\widehat{\beta}_0,\widehat{\vec{\beta}}})=\inf_{\beta_0\in\mathbb{R},\vec{\beta}\in\mathbb{R}^d}\color{red}{{\cal L}(\beta_0,\vec{\beta})}.\]
- Ex: The 1st simulated data 👉
Code
def log_loss(beta1, beta2, X, y, beta0 = 0.1):
beta_ = np.array([beta0, beta1, beta2])
sig = sigmoid(X @ beta_)
loss = np.mean(y*np.log(sig) + (1-y)*np.log(1-sig))
return -loss
beta1 = np.linspace(-7,2,25)
beta2 = np.linspace(-2,7,30)
losses = np.array([[log_loss(b1, b2, X=x1, y=y_) for b1 in beta1] for b2 in beta2])
bright_blue1 = [[0, '#235b63'], [1, '#45e696']]
fig = go.Figure(go.Surface(
x=beta1, y=beta2, z=losses, name="Loss function",
colorscale=bright_blue1,
hovertemplate='beta1: %{x}<br>' +
'beta2: %{y}<br>' +
'Loss: %{z}<extra></extra>'))
fig.update_layout(
scene = dict(
xaxis_title= 'beta1',
yaxis_title= 'beta2',
zaxis_title='Loss'),
width=450, height=300, title="Loss function of the 1st dataset")
fig.show()Binary Logistic Regression
Properties of The Loss
- Log loss \({\cal L}:\mathbb{R}^{d+1}\to \mathbb{R}\) is convex [See: D. Jurafsky and J. H. Martin (2023)].
- Consequence: There exists a unique \((\color{green}{\widehat{\beta}_0,\widehat{\vec{\beta}}})\) that minimizes the loss \({\cal L}\), i.e.,
\[(\color{green}{\widehat{\beta}_0,\widehat{\vec{\beta}}})=\arg\min_{\beta_0\in\mathbb{R},\vec{\beta}\in\mathbb{R}^d}\color{red}{{\cal L}(\beta_0,\vec{\beta})}.\]
😭 Unfortunately, such minimizer values \((\color{green}{\widehat{\beta}_0,\widehat{\vec{\beta}}})\) cannot be analytically computed.
😊 Fortunately, it can be numerically approximated!
Binary Logistic Regression
Properties of The Loss (Continous)
- If \(P=(p_1,\dots,p_d)\) and \(Q=(q_1,\dots,q_d)\) are two probability vectors, then Kullback–Leibler (KL) divergence between \(P\) and \(Q\) is defined by \[\color{blue}{\text{KL}(P\|Q)}=\sum_{j=1}^dp_j\log\Big(\frac{p_j}{q_j}\Big)\]
- It measures disimilarity between \(P\) and \(Q\).
- Ex: \(P_1=(0.6, 0.3, 0.1),P_2=(0.5, 0.2, 0.3)\) and \(Q=(0.3, 0.4, 0.3)\)
- \(\text{KL}(P_1\|Q)=\) 0.21972,
- \(\text{KL}(P_2\|Q)=\) 0.11678 (suggesting that \(P_2\) is more similar to \(Q\) than \(P_1\)).
- \(\text{KL}(P\|Q)\geq 0\) for any probability vectors \(P,Q\).
- \(\text{KL}(P\|Q)= 0\Leftrightarrow P=Q\).
- Note that, in general: \(\text{KL}(P\|Q)\neq \text{KL}(Q\|P)\).
- For any probab. vectors \(P\) and \(Q\): \(\color{red}{\text{CEn}(P,Q)}=-\sum_{j=1}^dp_j\log(q_j)\geq \color{blue}{\text{KL}(P\|Q)}, (Q:\text{ model})\).
Binary Logistic Regression
Summary
Logistic Regression Model
- Main assumption: \(p(1|\text{x})=1/(1+e^{-\color{green}{z}})=1/(1+e^{-\color{green}{(\beta_0+\text{x}^T\vec{\beta})}})\).
- Interpretation:
- Boundary decision is
Linear(hyperplane) defined by \(\beta_0\) and \(\vec{\beta}\). - Probability of being in each class depends on the relative distance of that point to the boundary.
- Works well when classes are linearly separable.
- Boundary decision is
- Interpretation:
- Objective: buliding a Logistic Regression model is equivalent to searching for parameters \(\beta_0\) and \(\vec{\beta}\) that minimizes the Log Loss function (Equation 1).
- The loss cannot be minimized analytically but can be minimized numerically.
Binary Logistic Regression
Polynomial Features
- Linear boundary assumption might be too weak in real situation.
- Polynomial features: \(X_1,\dots,X_d\to X_i^kX_j^{p-k}, k=0,1,\dots,p\).
- Original data:
| x1 | x2 | |
|---|---|---|
| 0 | -0.752759 | 2.704286 |
| 1 | 1.391964 | 0.591951 |
| 2 | -2.063888 | -2.064033 |
- Poly. features:
| x1 | x2 | x1^2 | x1 x2 | x2^2 | |
|---|---|---|---|---|---|
| 0 | -0.752759 | 2.704286 | 0.566647 | -2.035676 | 7.313162 |
| 1 | 1.391964 | 0.591951 | 1.937563 | 0.823974 | 0.350406 |
| 2 | -2.063888 | -2.064033 | 4.259634 | 4.259933 | 4.260232 |
Binary Logistic Regression
Polynomial Features
- Linear boundary assumption might be too weak in real situation.
- Polynomial features: \(X_1,\dots,X_d\to X_i^kX_j^{p-k}, k=0,1,\dots,p\).
- Offer more flexible boundaries.
- May be more suitable in complex problems.
- Higher risk of overfitting!!!
- Overfitting: happens when a model learns the training data too well, capturing noise and fluctuations rather than the underlying pattern.
Binary Logistic Regression
Gradient
Gradient
- If \(L:\mathbb{R}^d\to\mathbb{R}, y=L(x_1,...,x_d)\) be a real-valued function of \(d\) real variables. For any point \(a\in\mathbb{R}^d\), the gradient of \(L\) at point \(a\) is a \(d\)-dimensional vector defined by \[\nabla L(a)=\begin{bmatrix}\frac{\partial L}{\partial x_1}(a)\\ \vdots\\ \frac{\partial L}{\partial x_d}(a)\end{bmatrix}.\]
- It is the direction (from the point \(a\)) with the fastest increasing rate of the function \(L\).
- Ex: \(f(x,y)=0.1x^4+0.5y^2\). Compute \(\nabla f(1,-1)\).
- One has \(\frac{\partial f}{\partial x}=0.4x^3\) and \(\frac{\partial f}{\partial y}=y\).
- Therefore, \(\nabla f(1,-1)=(0.4,-1).\)
- Meaning: from point \((1,-1)\), function \(f\) increases fastest along the direction \((0.4, -1)\).
- Around 1847, Augustin-Louis Cauchy used this to propose a genius algorithm that makes impossibilities, possible!
Binary Logistic Regression
Gradient Descent Algorithm (GD)
Moving opposite to the gradient
- If \(L\) is the loss function, then our goal is to find its lowest position.
- Consider \(\theta_0\in\mathbb{R}^d\) and if \(L\) is differentiable, we can approximate \(L\) by a linear form around \(\theta_0\): \[L(\color{green}{\theta_0+h})\approx L(\color{red}{\theta_0})+\nabla L(\theta_0)^Th.\]
- If \(h=-\eta\nabla L(\theta_0)\) for some \(\eta>0\), we have: \(L(\color{green}{\theta_0-\eta\nabla L(\theta_0)})\approx L(\color{red}{\theta_0})-\eta\|\nabla L(\theta_0)\|^2\leq L(\theta_0).\)
- Interpretation: The loss \(L(\color{green}{\theta_0-\eta\nabla L(\theta_0)})\) is likely to be lower than \(L(\color{red}{\theta_0})\), therefore in searching for the lowest positoin of \(L\), we should move from \(\color{red}{\theta_0}\to\color{green}{\theta_0-\eta\nabla L(\theta_0)}\). This is the main idea of GD algorithm.
Gradient Descent Algorithm:- Initialization:
- learning rate: \(\eta>0\) (small \(\approx 0.001\) or \(0.01\))
- initial value: \(\theta_0\)
- Maximum iteration: \(N\)
- Stopping threshold: \(\delta>0\) (small \(< 10^{-5}\)).
- Update:
for t=1,2,...,N: \[\color{green}{\theta_{t}:=\theta_{t-1}-\eta\nabla L(\theta_{t-1})}.\]if\(\|\nabla L(\theta_{t^*})\|<\delta\) at some step \(t^*\):return\(\color{green}{\theta_{t^*}}\).else: return\(\color{green}{\theta_{N}}\).
- Initialization:
Binary Logistic Regression
Gradient Descent Algorithm (GD)
Binary Logistic Regression
Stochastic Gradient Descent (SGD)
Stochastic Gradient Descent (SGD) Algorithm
- Recall that for Logistic Regression, log loss may be normalized as the following average: \[\color{red}{{\cal L}(\beta_0,\vec{\beta})}=-\color{red}{\frac{1}{n}\sum_{i=1}^n}\left[y_i\log(p(1|\text{x}_i))+(1-y_i)\log(p(0|\text{x}_i))\right]:=\color{red}{\frac{1}{n}\sum_{i=1}^n}\ell(y_i,\hat{y}_i).\]
- In GD, the gradient \(\nabla {\cal L}\) is computed using the whole training data, which is very costly for large datasets.
- Using statistics, at each iteration \(t=1,\dots,N\), we can approximate \(\color{red}{\frac{1}{n}\sum_{i=1}^n}\) in the loss by \(\color{green}{\frac{1}{|B_t|}\sum_{i\in B_t}}\) using some random subset \(B_t\subset \{1,\dots,n\}\) (called minibatch), i.e., \(\color{red}{{\cal L}(\beta_0,\vec{\beta})}\approx\color{green}{\widehat{\cal L}(\beta_0,\vec{\beta})}=\color{green}{\frac{1}{|B_t|}\sum_{i\in B_t}}\ell(y_i,\hat{y}_i)\).
- Stochastic Gradient Descent Algorithm: (In Logistic Regression: \(\theta=(\beta_0,\vec{\beta})\))
- Initialize: \(\eta, N, \theta_0, \delta>0\) (same as in GD), and minibatch size \(b=|B_t|,\forall t=1,2,...,N\).
- Main loop:
for i=1,2,...,N:\[\color{green}{\theta_{t}}:=\color{red}{\theta_{t-1}}-\eta\nabla\color{green}{\widehat{\cal L}}(\color{red}{\theta_{t-1}}).\]
- Ex: Consider 1st simuated data 👉
Binary Logistic Regression
Stochastic Gradient Descent (SGD) in Action
Binary Logistic Regression
Gradient of Log Loss
Optimizing Log Loss in Logistic Regression
- Log loss for any \(\beta_0,\vec{\beta}\in\mathbb{R}^d: {\cal L}(\beta_0,\vec{\beta})=-\frac{1}{n}\sum_{i=1}^n[y_i\log(p(1|\text{x}_i))+(1-y_i)\log(p(0|\text{x}_i))]\).
- You should verify that:
- \(\partial_{\beta_0} {\cal L}(\beta_0,\vec{\beta})=\frac{1}{n}\sum_{i=1}^n\partial_{\beta_0} \ell(y_i,\hat{y}_i)=-\frac{1}{n}\sum_{i=1}^n(y_i-p(1|\text{x}_i))\in\mathbb{R}\).
- \(\nabla_{\vec{\beta}} {\cal L}(\beta_0,\vec{\beta})=\frac{1}{n}\sum_{i=1}^n\nabla_{\vec{\beta}} \ell(y_i,\hat{y}_i)=-\frac{1}{n}\sum_{i=1}^n\underbrace{(y_i-p(1|\text{x}_i))}_{\in\mathbb{R}}\underbrace{\text{x}_i}_{\in\mathbb{R}^d}\).
- We define
sigmoid function\(\sigma\) and the above gradient function oflog lossas follow:
GDcode is given in the next panel.SGDcan be implemented easily from thisGDcode.
d = 3 # input dimension of X
def grad_desc(grad, X, y, theta0 = [0]*(d+1),
max_Iter = 100, lr = 0.1, threshold = 1e-10):
if theta0 is None:
val = [np.random.uniform(-10, 10, size=d)]
else:
val = [np.array(theta0)]
grads = [grad(theta0, X, y)]
for i in range(max_Iter):
if np.sum(np.abs(grads[-1])) < threshold:
return np.row_stack(val), np.row_stack(grads)
new = val[-1] - lr * grads[-1]
val.append(new)
gr = grad(new)
grads.append(gr)
return np.row_stack(val), np.row_stack(grads)Binary Logistic Regression
More about gradient-based optimizations
- An overview of gradient descent optimization algorithms by S. Ruder (2016)
- Introductory, general ideas and implementation
- Less theories
- Gradient-Based Optimizer (GBO): A Review, Theory, Variants, and Applications by Daoud, M.S., Shehab, M., Al-Mimi, H.M. et al. (2023)
- Both explanation and theoretical
- Recent Advances in Stochastic Gradient Descent in Deep Learning by Tian, Y.; Zhang, Y.; Zhang, H. (2023)
- More detailed with implementation
- Less theories
Regularization
Why Regularization?
- In many cases, linear assumption is not suitable.
- However, when a model is too flexible, it’s risky of overfitting.
- Building a
good modelis capturing thepattern of data,NOTto fit all the training points.
- The effect of controlling parameters:
Regularization/penalization
\(L_2\) Penalization
- \(L_2\) regularized loss function: for any \(\alpha>0\), \[{\cal L}_2(\beta_0,\vec{\beta})=\underbrace{\color{red}{{\cal L}(\beta_0,\vec{\beta})}}_{\text{loss function}}+\alpha\underbrace{\color{green}{\sum_{j=0}^d\beta_j^2}}_{\text{Control}}.\]
- \(\alpha\) is called
regularization strength. Large\(\alpha\Leftrightarrow\)strongpenalization \(\Leftrightarrow\)small\(\beta_0,\vec{\beta}\).Small\(\alpha\Leftrightarrow\)lightpenalization \(\Leftrightarrow\)large\(\beta_0,\vec{\beta}\).
- \(\alpha\) is called
- Parameter \(\alpha\) balances
goodness of fit(loss \(\color{red}{{\cal L}}\)) and flexibility of the model (\(\color{green}{\sum_{j=0}^d\beta_j^2}\)). - 🔑 Key idea: Tune a suitable penalization strength \(\alpha\) that balances these two terms.
Regularization/penalization
\(L_1\) Penalization
- \(L_1\) regularized loss function: for any \(\alpha>0\), \[{\cal L}_1(\beta_0,\vec{\beta})=\underbrace{\color{red}{{\cal L}(\beta_0,\vec{\beta})}}_{\text{loss function}}+\alpha\underbrace{\color{green}{\sum_{j=0}^d|\beta_j|}}_{\text{Control}}.\]
- By its nature, \(L_1\) regularization performs
variable selection. - It tends to force unimportant components/variables to be \(0\).
- 🔑 Key idea: Tune a suitable penalization strength \(\alpha\).
- Remark:
Regularizationis an important method that can be used with any parametric models not only logtistic regression.
Regularization/penalization
Tuning polynomial degree
Tuning Optimal Polynomial Degree using \(10\)-fold Cross-Validation
from sklearn.metrics import accuracy_score
from sklearn.model_selection import cross_val_score
# List of degrees to search over
degrees = list(range(1,11))
# List for storing accuracy
acc = []
for deg in degrees:
poly = PolynomialFeatures(degree=deg, include_bias=False)
x_poly = poly.fit_transform(
pd.DataFrame(x1[:,1], columns=['x1'])
)
x_poly = np.column_stack([x_poly,x1[:,2],x1[:,1]*x1[:,2]])
# model
model = LogisticRegression()
score = cross_val_score(model, x_poly, y_, cv=10,
scoring='accuracy'
).mean()
acc.append(score)Regularization/penalization
Tuning Penalty Strength \(\alpha\) in \(L_2\) Penalty
Tuning Penalty Strength \(\alpha\) using \(10\)-fold Cross-Validation
from sklearn.metrics import accuracy_score
from sklearn.model_selection import cross_val_score
# Data
poly = PolynomialFeatures(degree=5, include_bias=False)
x_poly = poly.fit_transform(
pd.DataFrame(x1[:,1], columns=['x1']))
x_poly = np.column_stack([x_poly,x1[:,2],x1[:,1]*x1[:,2]])
# Penalty strength
alphas = np.concatenate([
np.linspace(1e-3,10, 50),
np.linspace(10.1, 1000, 50)]
)
coefficients = {f'{alp}': [] for alp in alphas}
acc = []
for alp in alphas:
# model
model = LogisticRegression(penalty="l2", C=1/alp)
score = cross_val_score(model, x_poly, y_, cv=10,
scoring='balanced_accuracy').mean()
acc.append(score)
# Fitting
model.fit(x_poly, y_)
coefficients[f'{alp}'] = model.coef_[0]Regularization/penalization
Tuning Penalty Strength \(\alpha\) in \(L_2\) Penalty
Tuning Penalty Strength \(\alpha\) using \(10\)-fold Cross-Validation
Regularization/penalization
Tuning Penalty Strength \(\alpha\) in \(L_1\) Penalty
Tuning Penalty Strength \(\alpha\) using \(10\)-fold Cross-Validation
from sklearn.metrics import accuracy_score
from sklearn.model_selection import cross_val_score
# Data
poly = PolynomialFeatures(degree=5, include_bias=False)
x_poly = poly.fit_transform(
pd.DataFrame(x1[:,1], columns=['x1']))
x_poly = np.column_stack([x_poly,x1[:,2],x1[:,1]*x1[:,2]])
# Penalty strength
alphas = np.concatenate([
np.linspace(1e-3,10, 50),
np.linspace(10.1, 1000, 50)]
)
coefficients = {f'{alp}': [] for alp in alphas}
acc = []
for alp in alphas:
# model
model = LogisticRegression(penalty="l1",
C=1/alp, solver='saga')
score = cross_val_score(model, x_poly, y_, cv=10,
scoring='balanced_accuracy').mean()
acc.append(score)
# Fitting
model.fit(x_poly, y_)
coefficients[f'{alp}'] = model.coef_[0]Regularization/penalization
Tuning Penalty Strength \(\alpha\) in \(L_1\) Penalty
Tuning Penalty Strength \(\alpha\) using \(10\)-fold Cross-Validation
Multinomial Logistic Regression
Example
- Task:
Predictingtarget \(y\in\{1,2,\dots,M\}\) using its input \(\text{x}\in\mathbb{R}^d\). - Example: Kaggle wine quality data.
| fixed.acidity | volatile.acidity | citric.acid | residual.sugar | chlorides | free.sulfur.dioxide | total.sulfur.dioxide | density | pH | sulphates | alcohol | quality | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
| 3 | 11.2 | 0.28 | 0.56 | 1.9 | 0.075 | 17.0 | 60.0 | 0.9980 | 3.16 | 0.58 | 9.8 | 6 |
| 7 | 7.3 | 0.65 | 0.00 | 1.2 | 0.065 | 15.0 | 21.0 | 0.9946 | 3.39 | 0.47 | 10.0 | 7 |
| 18 | 7.4 | 0.59 | 0.08 | 4.4 | 0.086 | 6.0 | 29.0 | 0.9974 | 3.38 | 0.50 | 9.0 | 4 |
| 267 | 7.9 | 0.35 | 0.46 | 3.6 | 0.078 | 15.0 | 37.0 | 0.9973 | 3.35 | 0.86 | 12.8 | 8 |
| 459 | 11.6 | 0.58 | 0.66 | 2.2 | 0.074 | 10.0 | 47.0 | 1.0008 | 3.25 | 0.57 | 9.0 | 3 |
- Goal: predict the quality of wine using its physicochemical tests.
Multinomial Logistic Regression
Example
- Task:
Predictingtarget \(y\in\{1,2,\dots,M\}\) using its input \(\text{x}\in\mathbb{R}^d\). - Example: Kaggle wine quality data.
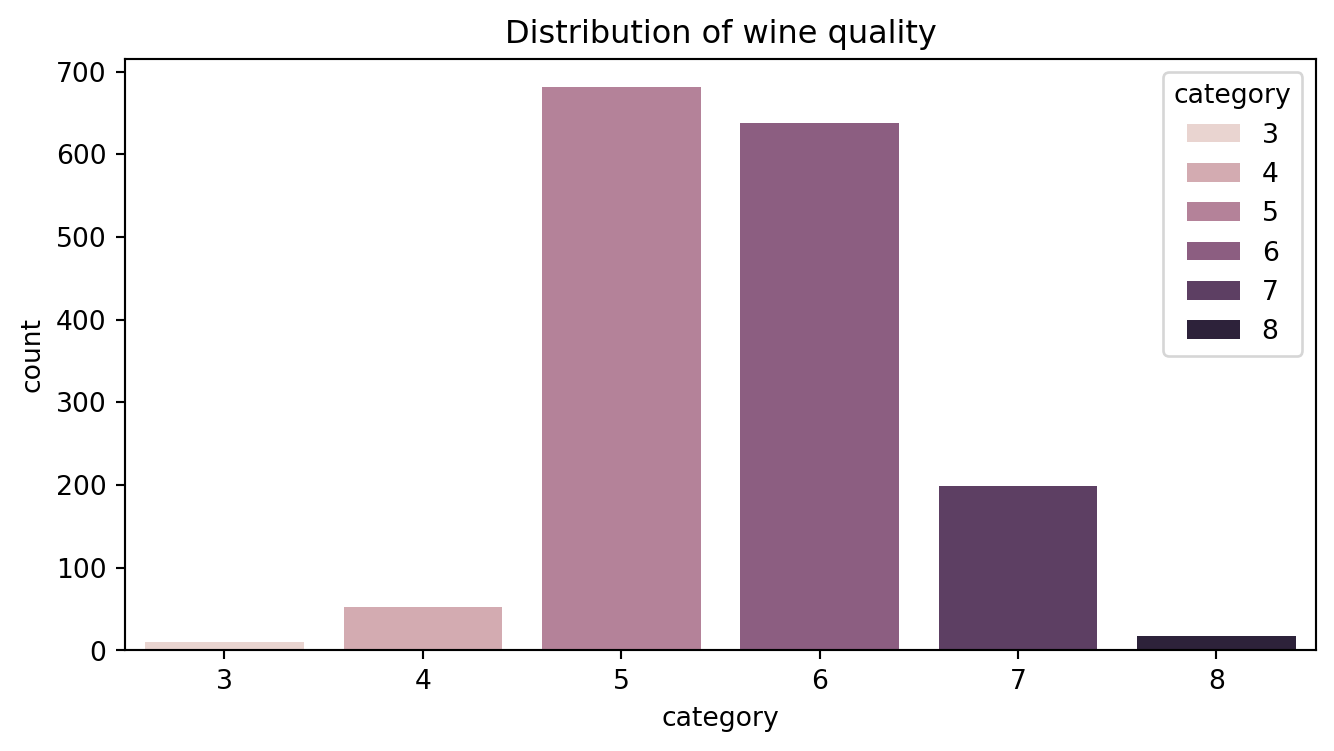
Multinomial Logistic Regression
Example (modified)
- Task:
Predictingtarget \(y\in\{1,2,\dots,M\}\) using its input \(\text{x}\in\mathbb{R}^d\). - Example: Kaggle wine quality data.
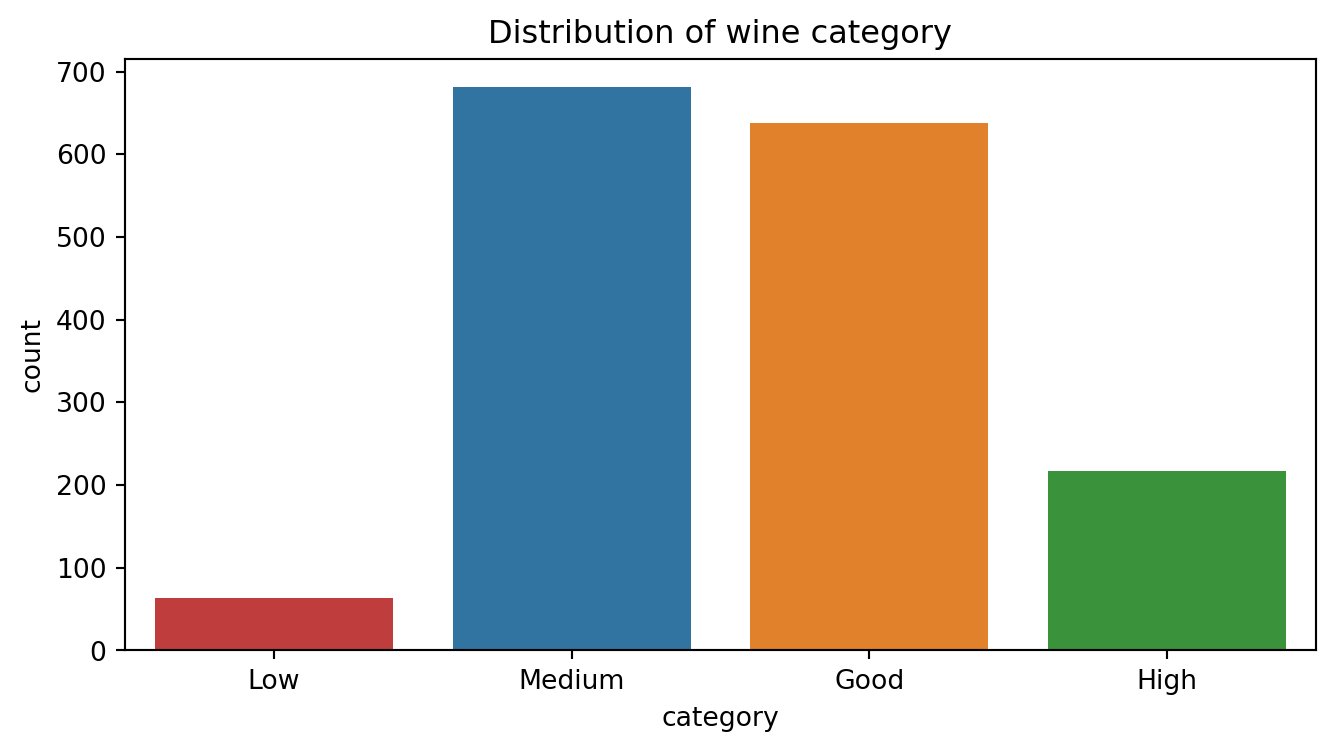
Multinomial Logistic Regression
Model
- In this case, \(y\) takes \(M\) distinct values, it’s often encoded to be \(M\)-dimensional vector: \[y=k\Leftrightarrow p=(0,\dots,0,\underbrace{1}_{k\text{th index}},0,\dots,0)^T.\]
- The model also returns \(M\)-dimensional probability vector where
indexwith highest probability is thepredicted class. - \(\text{Softmax}:\mathbb{R}^M\to\mathbb{S}_{M-1}=\{p_j\in[0,1]^M:\sum_{j=1}^Mp_j=1\}\) defined by \[\vec{z}\mapsto \vec{s}=\text{Softmax}(z)=\Big(\frac{e^{z_1}}{\sum_{j=1}^Me^{z_j}},\dots,\frac{e^{z_M}}{\sum_{j=1}^Me^{z_j}}\Big).\]
- It converts any \(M\)-dimensional vector \(\vec{z}\) to \(M\)-dimensional probability vector \(\vec{s}\).
Multinomial Logistic Regression
Model
- \(\text{Softmax}:\mathbb{R}^M\to\mathbb{S}_{M-1}=\{p_j\in[0,1]^M:\sum_{j=1}^Mp_j=1\}\) defined by \[\vec{z}\mapsto \vec{s}=\text{Softmax}(z)=\Big(\frac{e^{z_1}}{\sum_{j=1}^Me^{z_j}},\dots,\frac{e^{z_M}}{\sum_{j=1}^Me^{z_j}}\Big).\]
- Model: Given parameter matrix \(\color{green}{W}\) of size \(M\times d\) and intercept vector \(\color{green}{\vec{b}}\in\mathbb{R}^d\), the predicted probability of any input data \(\text{x}_i\in\mathbb{R}^d\) is defined by

\[\begin{align*}\color{red}{\hat{p}_i}&=\text{Softmax}(\color{green}{W}\text{x}_i+\color{green}{\vec{b}})\\ &=\text{Softmax}\begin{pmatrix} \color{green}{\begin{bmatrix}w_{11}& \dots & w_{1d}\\ w_{11}& \dots & w_{1d}\\ \vdots & \vdots & \vdots\\ w_{M1}& \dots & w_{Md}\end{bmatrix}}\begin{bmatrix}x_{i1}\\ x_{i2}\\ \vdots\\ x_{id}\end{bmatrix}+\color{green}{\begin{bmatrix}b_{1}\\ b_{2}\\ \vdots\\ b_{M}\end{bmatrix}}\end{pmatrix}=\color{red}{\begin{bmatrix}p_{i1}\\ p_{i2}\\ \vdots\\ p_{iM}\end{bmatrix}}\end{align*}\]
Multinomial Logistic Regression
Model

\[\begin{align*}\color{red}{\hat{p}_i}&=\text{Softmax}(\color{green}{W}\text{x}_i+\color{green}{\vec{b}})\\ &=\text{Softmax}\begin{pmatrix} \color{green}{\begin{bmatrix}w_{11}& \dots & w_{1d}\\ w_{11}& \dots & w_{1d}\\ \vdots & \vdots & \vdots\\ w_{M1}& \dots & w_{Md}\end{bmatrix}}\begin{bmatrix}x_{i1}\\ x_{i2}\\ \vdots\\ x_{id}\end{bmatrix}+\color{green}{\begin{bmatrix}b_{1}\\ b_{2}\\ \vdots\\ b_{M}\end{bmatrix}}\end{pmatrix}=\color{red}{\begin{bmatrix}p_{i1}\\ p_{i2}\\ \vdots\\ p_{iM}\end{bmatrix}}\end{align*}\]

Multinomial Logistic Regression
Cross-entropy loss
- We search for best possible parameters \(\color{green}{W}\in\mathbb{R}^{M\times d}\) and \(\color{green}{\vec{b}}\in\mathbb{R}^d\) by minimizing
Cross Entropyloss defined below: \[\text{CEn}(W,\vec{b})=-\sum_{i=1}^n\sum_{m=1}^M\color{blue}{p_{im}}\log(\color{red}{\hat{p}_{im}}),\text{ where }\color{red}{\widehat{\text{p}}_i}=(\color{red}{\hat{p}_{i1}},\color{red}{\dots},\color{red}{\hat{p}_{iM}})\text{ is the predicted probability of }\color{blue}{\text{p}_i}.\]
Multinomial Logistic Regression
Gradient of Cross-Entropy
Optimizing Cross-entropy in Multinomial Logistic Regression
- Cross Entropy of any parameter \(\color{green}{W}\in\mathbb{R}^{M\times d}\) and \(\color{green}{\vec{b}}\in\mathbb{R}^d\): \(\text{CEn}(\color{green}{W},\color{green}{\vec{b}})=-\sum_{i=1}^n\sum_{m=1}^M\color{blue}{p_{im}}\log(\color{red}{\widehat{p}_{im}})\).
- Challenge: Show that
- \(\nabla_{\color{green}{\vec{b}}} \text{CEn}(\color{green}{W},\color{green}{\vec{b}})=\sum_{i=1}^n\nabla_{\color{green}{\vec{b}}} \ell(\color{blue}{\text{p}_i},\color{red}{\hat{\text{p}}_i})=-\sum_{i=1}^n\underbrace{(\color{blue}{\text{p}_i}-\text{softmax}(\color{green}{W}\text{x}+\color{green}{\vec{b}}))}_{\in\mathbb{R}^d}\).
- \(\nabla_{\color{green}{W}} \text{CEn}(\color{green}{W},\color{green}{\vec{b}})=\sum_{i=1}^n\nabla_{\color{green}{W}} \ell(\color{blue}{\text{p}_i},\color{red}{\widehat{p}_i})=-\sum_{i=1}^n\underbrace{(\color{blue}{\text{p}_i}-\color{red}{\widehat{\text{p}}_i})}_{\in\mathbb{R}^{d\times 1}}\underbrace{\text{x}_i^T}_{\in\mathbb{R}^{1\times d}}=\underbrace{(\color{red}{\widehat{P}}-\color{blue}{P})^TX}_{\in\mathbb{R}^{d\times d}}\), where
\[\begin{align*} \color{red}{\hat{P}}=\color{red}{\underbrace{\begin{bmatrix} \hat{p}_{11} &\dots & \hat{p}_{1d}\\ \vdots & \vdots & \vdots\\ \hat{p}_{n1} &\dots & \hat{p}_{nd} \end{bmatrix}}_{\text{Matrix of predicted probab}}}, \color{blue}{P}=\color{blue}{\underbrace{\begin{bmatrix} p_{11} &\dots & p_{1d}\\ \vdots & \vdots & \vdots\\ p_{n1} &\dots & p_{nd} \end{bmatrix}}_{\text{One-hot encoded matrix of $y_i$}}}\text{ and } X=\underbrace{\begin{bmatrix} x_{11} &\dots & x_{1d}\\ \vdots & \vdots & \vdots\\ x_{n1} &\dots & x_{nd} \end{bmatrix}}_{\text{Matrix of inputs $x_i$}} \end{align*}\]
Further reading: J. Chiang (2023) and K. Stratos (2018).
Multinomial Logistic Regression
In action: Kaggle wine quality data
| fixed.acidity | volatile.acidity | citric.acid | residual.sugar | chlorides | free.sulfur.dioxide | total.sulfur.dioxide | density | pH | sulphates | alcohol | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| fixed.acidity | 1.000000 | -0.256000 | 0.672000 | 0.115000 | 0.094000 | -0.154000 | -0.113000 | 0.668000 | -0.683000 | 0.183000 | -0.062000 |
| volatile.acidity | -0.256000 | 1.000000 | -0.552000 | 0.002000 | 0.061000 | -0.011000 | 0.076000 | 0.022000 | 0.235000 | -0.261000 | -0.202000 |
| citric.acid | 0.672000 | -0.552000 | 1.000000 | 0.144000 | 0.204000 | -0.061000 | 0.036000 | 0.365000 | -0.542000 | 0.313000 | 0.110000 |
| residual.sugar | 0.115000 | 0.002000 | 0.144000 | 1.000000 | 0.056000 | 0.187000 | 0.203000 | 0.355000 | -0.086000 | 0.006000 | 0.042000 |
| chlorides | 0.094000 | 0.061000 | 0.204000 | 0.056000 | 1.000000 | 0.006000 | 0.047000 | 0.201000 | -0.265000 | 0.371000 | -0.221000 |
| free.sulfur.dioxide | -0.154000 | -0.011000 | -0.061000 | 0.187000 | 0.006000 | 1.000000 | 0.668000 | -0.022000 | 0.070000 | 0.052000 | -0.069000 |
| total.sulfur.dioxide | -0.113000 | 0.076000 | 0.036000 | 0.203000 | 0.047000 | 0.668000 | 1.000000 | 0.071000 | -0.066000 | 0.043000 | -0.206000 |
| density | 0.668000 | 0.022000 | 0.365000 | 0.355000 | 0.201000 | -0.022000 | 0.071000 | 1.000000 | -0.342000 | 0.149000 | -0.496000 |
| pH | -0.683000 | 0.235000 | -0.542000 | -0.086000 | -0.265000 | 0.070000 | -0.066000 | -0.342000 | 1.000000 | -0.197000 | 0.206000 |
| sulphates | 0.183000 | -0.261000 | 0.313000 | 0.006000 | 0.371000 | 0.052000 | 0.043000 | 0.149000 | -0.197000 | 1.000000 | 0.094000 |
| alcohol | -0.062000 | -0.202000 | 0.110000 | 0.042000 | -0.221000 | -0.069000 | -0.206000 | -0.496000 | 0.206000 | 0.094000 | 1.000000 |
Multinomial Logistic Regression
In action: Target vs Inputs
Code
sns.set(style="whitegrid")
_, axs = plt.subplots(2,3,figsize=(10,5))
i = 0
for var in df_wine.columns[:6]:
sns.boxplot(df_wine, x="category", y=var,
hue="category", ax=axs[i//3, i%3],
order=['Low', 'Medium', 'Good', 'High'])
axs[i//3, i%3].set_title(f"Category vs {var}")
i += 1
plt.tight_layout()
plt.show()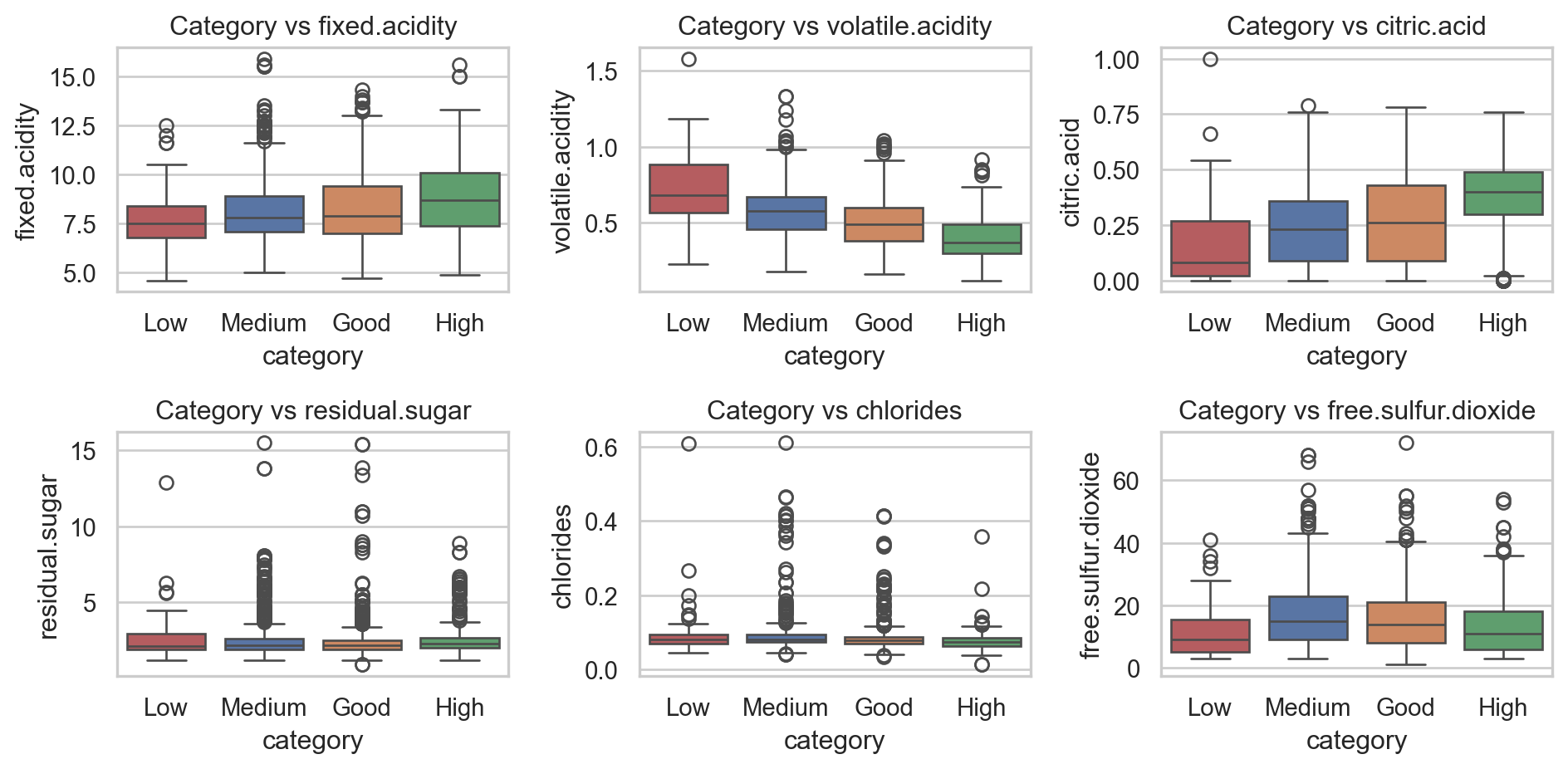
Multinomial Logistic Regression
In action: Target vs Inputs
Code
from matplotlib.gridspec import GridSpec
fig = plt.figure(figsize=(10,5))
gs = GridSpec(4, 6)
axs = []
i = 0
for var in df_wine.columns[6:-2]:
if i < 2:
axs.append(fig.add_subplot(gs[:2, (2*i % 6):(2*i+2)%6]))
elif i == 2:
axs.append(fig.add_subplot(gs[:2, 4:]))
elif i == 3:
axs.append(fig.add_subplot(gs[2:, 1:3]))
else:
axs.append(fig.add_subplot(gs[2:, 3:5]))
sns.boxplot(df_wine, x="category", y=var,
hue="category", ax=axs[-1],
order=['Low', 'Medium', 'Good', 'High'])
axs[-1].set_title(f"Category vs {var}")
i += 1
plt.tight_layout()
plt.show()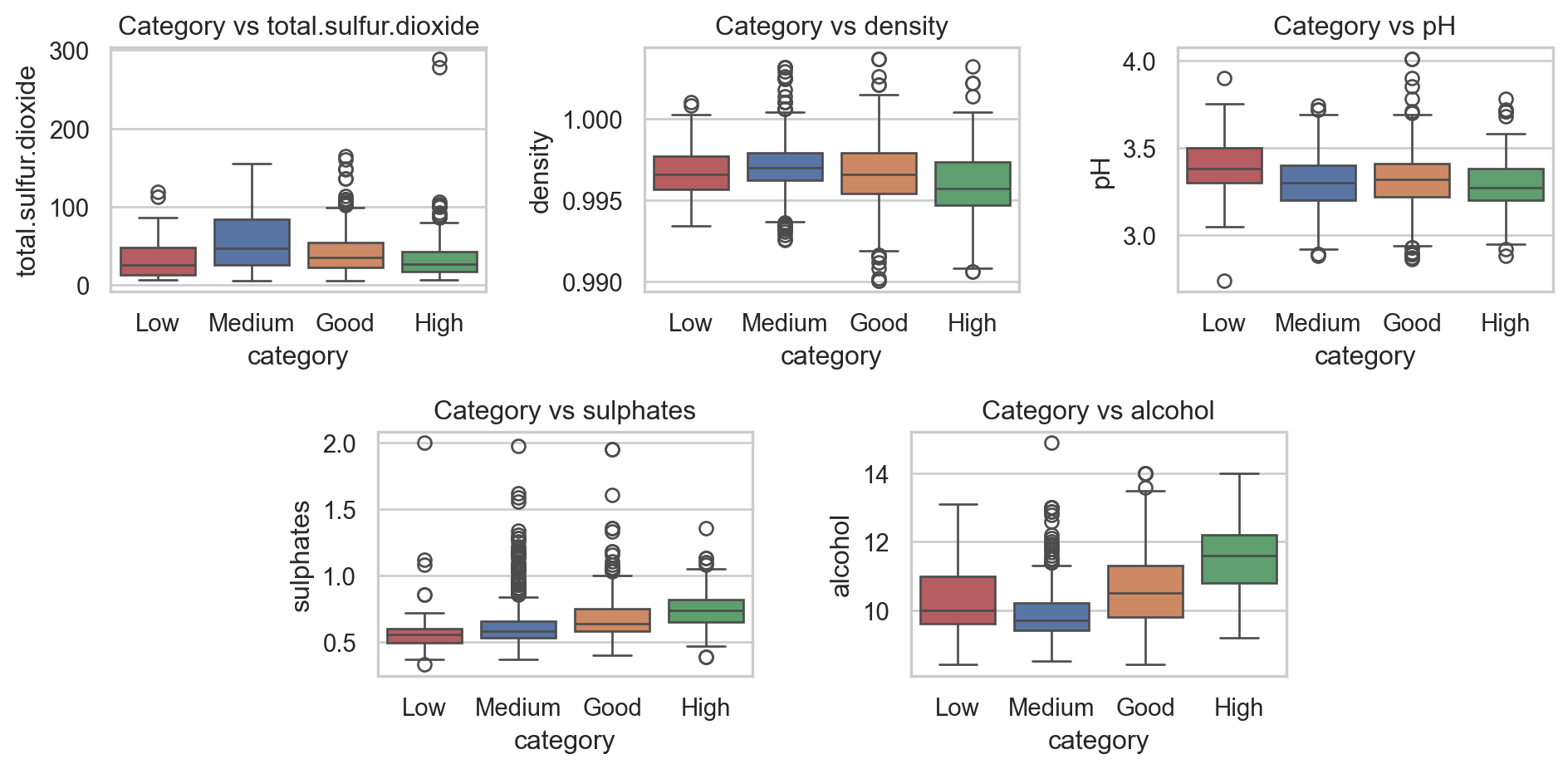
Multinomial Logistic Regression
In action: Kaggle wine quality data
Multinomial Logistic Regression
from sklearn.preprocessing import MinMaxScaler, PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, balanced_accuracy_score, f1_score, recall_score, precision_score, log_loss, confusion_matrix, ConfusionMatrixDisplay
# Train test split
X_wine_train, X_wine_test, y_wine_train, y_wine_test = train_test_split(
df_wine.iloc[:,:-2], df_wine['category'], test_size=0.25,
stratify=df_wine['category'],
random_state=42)
# Scaling data
scaler = MinMaxScaler()
# Fitting the model
X_wine_train = scaler.fit_transform(X_wine_train)
X_wine_test = scaler.transform(X_wine_test)
lgr = LogisticRegression(max_iter=300)
lgr_fit = lgr.fit(X_wine_train, y_wine_train)
y_hat_test1 = lgr_fit.predict(X_wine_test)
performance1 = pd.DataFrame( {
'Acc': [accuracy_score(y_wine_test, y_hat_test1)],
'Balanced Acc': [balanced_accuracy_score(y_wine_test, y_hat_test1)],
'Precision': [precision_score(y_wine_test, y_hat_test1, average="macro")],
'Recall': [recall_score(y_wine_test, y_hat_test1, average="macro")],
'F1-score': [f1_score(y_wine_test, y_hat_test1, average="macro")] }, index=['Logit'])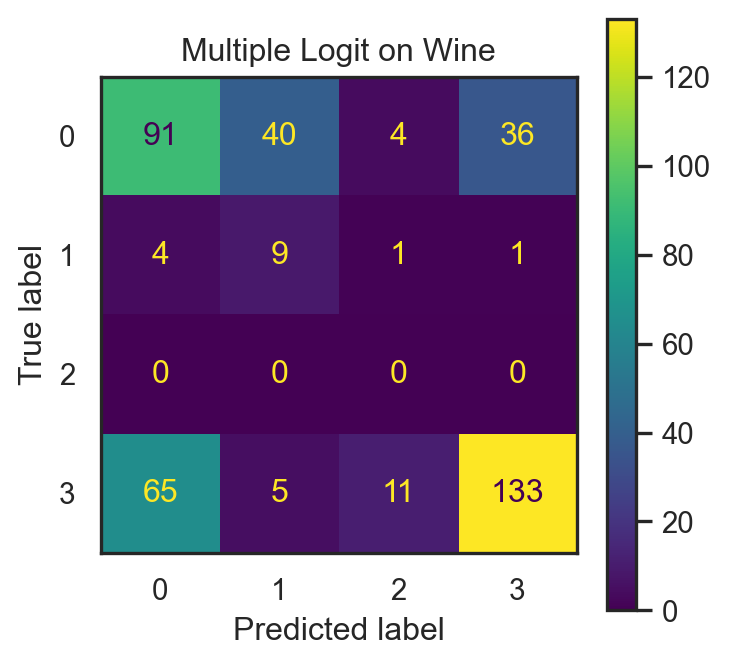
| Acc | Balanced Acc | Precision | Recall | F1-score | |
|---|---|---|---|---|---|
| Logit | 0.5825 | 0.379442 | 0.438415 | 0.379442 | 0.375857 |
Multinomial Logistic Regression
In action: Kaggle wine quality data
Multinomial Logistic Regression with Polynomial Features
degree = list(range(2,9,2))
# List to store all losses
poly_loss, poly_test_loss, test_loss = [], [], {}
for deg in degree:
pf = PolynomialFeatures(degree=deg)
X_poly = pf.fit_transform(X_wine_train)
model = LogisticRegression(max_iter=300)
score = -cross_val_score(model, X_poly, y_wine_train, cv=10,
scoring='neg_log_loss').mean()
poly_loss.append(score)
# Fit and predict
model = model.fit(X_poly, y_wine_train)
X_poly_test = pf.transform(X_wine_test)
y_hat_test = model.predict(X_poly_test)
prob = model.predict_proba(X_poly_test)
poly_test_loss.append(log_loss(y_wine_test, prob))
test_loss['Acc'] = [accuracy_score(y_wine_test, y_hat_test)]
test_loss['Balanced Acc'] = [balanced_accuracy_score(y_wine_test, y_hat_test)]
test_loss['Precision'] = [precision_score(y_wine_test, y_hat_test, average="macro")]
test_loss['Recall'] = [recall_score(y_wine_test, y_hat_test, average="macro")]
test_loss['F1-score'] = [f1_score(y_wine_test, y_hat_test, average="macro")]
performance1 = pd.concat([performance1, pd.DataFrame(test_loss, index=[f'Poly {deg}'])])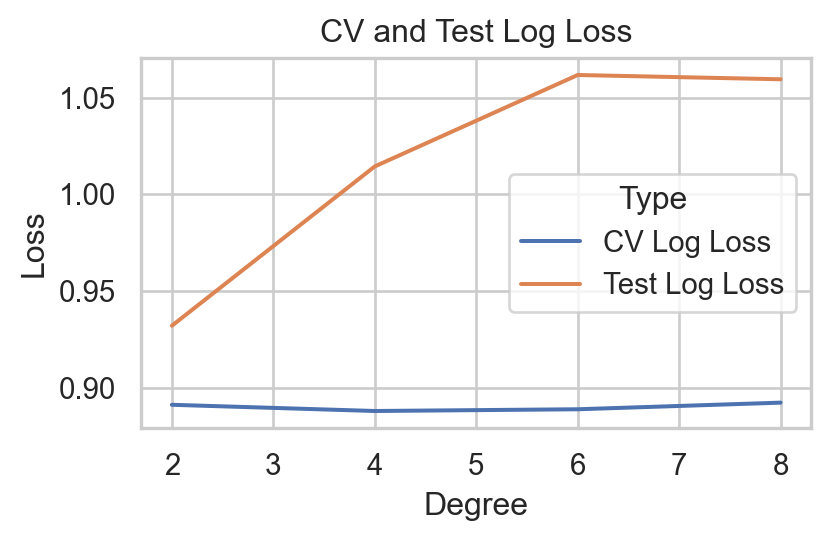
| Acc | Balanced Acc | Precision | Recall | F1-score | |
|---|---|---|---|---|---|
| Logit | 0.5825 | 0.379442 | 0.438415 | 0.379442 | 0.375857 |
| Poly 2 | 0.5850 | 0.407704 | 0.708400 | 0.407704 | 0.426100 |
| Poly 4 | 0.5925 | 0.432772 | 0.711266 | 0.432772 | 0.464086 |
| Poly 6 | 0.5925 | 0.435747 | 0.707423 | 0.435747 | 0.467052 |
| Poly 8 | 0.5925 | 0.435747 | 0.707353 | 0.435747 | 0.467121 |
Multinomial Logistic Regression
In action: Kaggle wine quality data
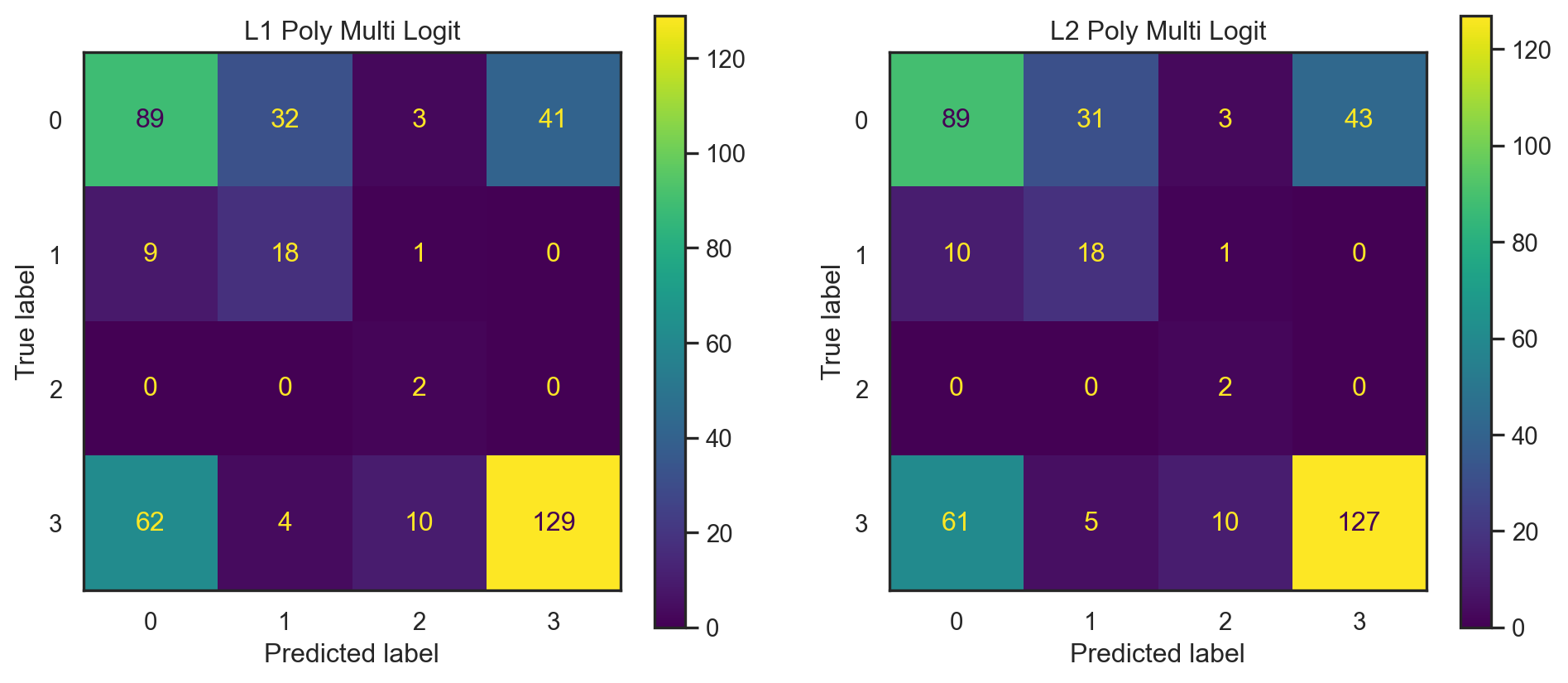
\(L_2\) Regularized Multinomial Logistic Regression with Polynomial Features
deg_opt = np.argmin(performance1['F1-score'][1:])
pf = PolynomialFeatures(degree=degree[deg_opt])
X_poly = pf.fit_transform(X_wine_train)
X_poly_test = pf.transform(X_wine_test)
alphas = list(np.linspace(1e-5, 1, 30)) + list(np.linspace(1.01, 10, 30))
# List to store all losses
poly_loss, poly_test_loss, test_loss = [], [], {}
coefs = {f'alpha:{alp}': [] for alp in alphas}
for alp in alphas:
model = LogisticRegression(penalty="l2", C=1/alp, max_iter=300)
score = -cross_val_score(model, X_poly, y_wine_train, cv=10,
scoring='neg_log_loss').mean()
poly_loss.append(score)
# Fit and predict
model = model.fit(X_poly, y_wine_train)
y_hat_test = model.predict(X_poly_test)
coefs[f'alpha:{alp}'] = model.coef_[0]
prob = model.predict_proba(X_poly_test)
poly_test_loss.append(log_loss(y_wine_test, prob))
test_loss['Acc'] = [accuracy_score(y_wine_test, y_hat_test)]
test_loss['Balanced Acc'] = [balanced_accuracy_score(y_wine_test, y_hat_test)]
test_loss['Precision'] = [precision_score(y_wine_test, y_hat_test, average="macro")]
test_loss['Recall'] = [recall_score(y_wine_test, y_hat_test, average="macro")]
test_loss['F1-score'] = [f1_score(y_wine_test, y_hat_test, average="macro")]
performance1 = pd.concat([performance1, pd.DataFrame(test_loss, index=[f'L2-Alp:{alp}'])])Multinomial Logistic Regression
In action: Kaggle wine quality data
\(L_1\) Regularized Multinomial Logistic Regression with Polynomial Features
alphas = list(np.linspace(1e-5, 1, 30)) + list(np.linspace(1.01, 10, 30))
# List to store all losses
poly_loss, poly_test_loss, test_loss = [], [], {}
coefs = {f'alpha:{alp}': [] for alp in alphas}
for alp in alphas:
model = LogisticRegression(penalty="l1", solver='saga', C=1/alp, max_iter=300)
score = -cross_val_score(model, X_poly, y_wine_train, cv=10,
scoring='neg_log_loss').mean()
poly_loss.append(score)
# Fit and predict
model = model.fit(X_poly, y_wine_train)
coefs[f'alpha:{alp}'] = model.coef_[0]
X_poly_test = pf.transform(X_wine_test)
y_hat_test = model.predict(X_poly_test)
prob = model.predict_proba(X_poly_test)
poly_test_loss.append(log_loss(y_wine_test, prob))
test_loss['Acc'] = [accuracy_score(y_wine_test, y_hat_test)]
test_loss['Balanced Acc'] = [balanced_accuracy_score(y_wine_test, y_hat_test)]
test_loss['Precision'] = [precision_score(y_wine_test, y_hat_test, average="macro")]
test_loss['Recall'] = [recall_score(y_wine_test, y_hat_test, average="macro")]
test_loss['F1-score'] = [f1_score(y_wine_test, y_hat_test, average="macro")]
performance1 = pd.concat([performance1, pd.DataFrame(test_loss, index=[f'L1-Alp:{alp}'])])Multinomial Logistic Regression
Summary
| Acc | Balanced Acc | Precision | Recall | F1-score | |
|---|---|---|---|---|---|
| Logit | 0.5825 | 0.379442 | 0.438415 | 0.379442 | 0.375857 |
| Poly 2 | 0.5850 | 0.407704 | 0.708400 | 0.407704 | 0.426100 |
| Poly 4 | 0.5925 | 0.432772 | 0.711266 | 0.432772 | 0.464086 |
| Poly 6 | 0.5925 | 0.435747 | 0.707423 | 0.435747 | 0.467052 |
| Poly 8 | 0.5925 | 0.435747 | 0.707353 | 0.435747 | 0.467121 |
| L2-Alp:0.138 | 0.5900 | 0.440411 | 0.695612 | 0.440411 | 0.470734 |
| L1-Alp:0.724 | 0.5950 | 0.443352 | 0.702880 | 0.443352 | 0.474235 |
Multinomial Logistic Regression
Summary
Pros & Cons
Pros
- Simplicity: It’s easy to understand and implement.
- Efficiency: It’s not so computationally expensive, making it suitable for large datasets.
- Interpretability: It converts relative distances from input data to boundary decision into probabilities, which can be meaningfully interpreted.
- No Scaling Required: It doesn’t require input features to be scaled or standardized (you can also tranform for efficient computation).
- Works Well with Linearly Separable Data: Performs well when the data is linearly separable.
Cons
- Assumes Linearity: Assumes a linear relationship between the independent variables and the log-odds of the dependent variable.
- Sensitivity to Outliers: Outliers can affect the model’s performance and accuracy.
- Overfitting: Can overfit if the dataset has a large number of features compared to the number of observations.
- Limited to Binary Outcomes: Standard logistic regression is designed for binary classification and may not perform as well with multiclass classification problems.
- Assumes Independence of Errors: Assumes that the observations are independent of each other and that there is no multicollinearity among predictors.
🥳 It’s party time 🥂
📋 View party menu here: Party 2 Menu.
🫠 Download party invitation here: Party 2 Invitation Letter.


