ទ្រឹស្តីតម្រែតម្រង់តម្លៃ (Regression Theory)

១. សេចក្តីផ្តើម

តម្រែតម្រង់តម្លៃ ឬ Regression សំដៅដល់កិច្ចការទាំងឡាយណាដែលយើងចង់ព្យាករណ៍តម្លៃនៃ output ជាចំនួនពិត (\(y\in\mathbb{R}\))។ មានកិច្ចការជាច្រើនដែលអាចចាត់ចូលជាប្រភេទតម្រែតម្រង់តម្លៃ ហើយលើសពីនេះទៅទៀត វាក៏មានលក្ខណៈទូទៅជាងបញ្ហាដែលមានទម្រង់ជា ការធ្វើចំណែកថ្នាក់បែបមានការណែនាំ (supervised classification) ផងដែរ ដោយសារគេអាចបម្លែងតម្លៃជាចំនួនពិតទៅជាប្រូបាបប៊ីលីតេនិង នាំទៅដល់ការធ្វើចំណែកថ្នាក់បានដោយងាយ ឬនិយាយម្យ៉ាងទៀតគឺថា ការធ្វើចំណែកថ្នាក់បែបមានការណែនាំជាទូទៅកើតចេញពីការកែច្នៃតម្រែតម្រង់តម្លៃ។ ហេតុនេះហើយ យើងចាប់ផ្តើមនិយាយពីទ្រឹស្តីសំខាន់ៗនៃតម្រែតម្រង់តម្លៃមុននឹងឈានទៅដល់ការសិក្សាម៉ូដែលផ្សេងៗសម្រាប់ដោះស្រាយបញ្ហបែបនេះ។

រូបទី១៖ តម្រែតម្រង់តម្លៃ (regression) និង ការធ្វើចំណែកថ្នាក់ដោយមានការណែនាំ (supervised classification) ។

ក្នុងអត្ថបទនេះ យើងនឹងសិក្សាពីប្រភេទរង្វាស់នៃកំហុសមួយប្រភេទដែលគេនិយមប្រើក្នុងការសិក្សាតម្រែតម្រង់តម្លៃហៅថា មធ្យមនៃលម្អៀងការ៉េ (Mean Squared Error) ហើយនិងម៉ូដែលដែលល្អបំផុតសម្រាប់ប្រើប្រាស់ជាមួយនឹងរង្វាស់កំហុសប្រភេទនេះ។ បើដឹងថាម៉ូដែលដែលល្អបំផុតជានរណាទៅហើយ ហេតុអ្វីបញ្ហាតម្រែតម្រង់តម្លៃនៅតែមានភាពស្មុគស្មាញទៀត? ក្រៅពីឆ្លើយសំនួរនេះ គោលដៅចម្បងគឺយើងចង់បង្ហាញពីបរមាភាពនៃម៉ូដែលដែលយើងហៅថាជាបរមាម៉ូដែលនេះតាមរយៈទ្រឹស្តីនិង ការគណនាផងដែរ។ យើងក៏នឹងស្គាល់ផងដែរពីធាតុសំខាន់ៗជាច្រើនដូចជា វុិចទ័រចៃដន្យ (random vector) និង សង្ឃឹមគណិតមានលក្ខខណ្ឌ (conditional expectation) នៃរបាយប្រូបាបមានវិមាត្រលើសពីមួយ។

សម្រាប់មិត្តអ្នកអាន៖ ប្រសិនបើមិត្តអ្នកអានមិនមែនជាអ្នកចូលចិត្តស្វែងយល់ពីមូលហេតុជាទ្រឹស្តីគណិតវិទ្យានៃបញ្ហាផ្សេងៗនោះទេ អត្ថបទនេះមិនមែនសម្រាប់ប្រិយមិត្តទេ។ ប្រិយមិត្តអាចអានត្រឹមផ្នែកទី២ដែលនិយាយអំពីការតាងទិន្នន័យហើយ រំលងទៅអានផ្នែកបន្ទាប់ដែលនិយាយអំពីម៉ូដែលតម្រែតម្រង់លីនេអ៊ែរតែម្តង។

២. ទិន្នន័យ

មុននឹងចូលដល់ការស្វែងយល់ពីមូលដ្ឋាននៃតម្រែតម្រង់តម្លៃនិង ម៉ូដែលនានាព្រមទាំងការសិក្សាសុីជម្រៅក្នុងសិក្ខាម៉ាសុីន យើងនឹងកំណត់តាងធាតុសំខាន់ៗមួយចំនួនដែលនឹងត្រូវប្រើប្រាស់ជាទូទៅសម្រាប់ការសិក្សានេះ។

យើងបានកំណត់តាងទិន្នន័យសម្រាប់បង្វឹកម៉ូដែលសិក្ខាម៉ាសុីនដោយ៖ \({\cal T}=\{(x_1,y_1),\dots, (x_n,y_n)\}\) ដែលមានផ្ទុក \(n\geq 1\) ទិន្នន័យហើយក្នុងនោះ គូ input-output \((x_i,y_i)\in\mathbb{R}^d\times{\cal Y}\) ចំពោះគ្រប់ \(i=1,...,n\) ។ ក្នុងករណីតម្រែតម្រង់តម្លៃយើងមាន \({\cal Y}=\mathbb{R}\) ហើយក្នុងករណីកិច្ចការធ្វើចំណែកថ្នាក់បែបមានការណែនាំយើងបាន \(\cal Y\) រាប់អស់និង មានចំនួនធាតុតូចបង្គួរ ។ យើងបានទិន្នន័យសម្រាប់បង្វឹកម៉ូដែល៖

\[{\cal T}=\left[\begin{array} \ x_{11} & x_{12} & \dots & x_{1d} & y_{1}\\ x_{21} & x_{22} & \dots & x_{1d} & y_{2}\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ x_{n1} & x_{n2} & \dots & x_{nd} & y_{n} \end{array}\right]\] ដែលក្នុងនោះ ជួរឈរនីមួយៗហៅថាអថេរឬ អញ្ញាត (variable) ហើយជាវុិចទ័រមានប្រវែង \(n\) កំណត់ដោយ៖ \[ X_j=\left(\begin{array} \ x_{1j} \\ x_{2j} \\ \vdots \\ x_{nj} \end{array}\right)\in\mathbb{R}^n, j=1,...,d\] ចំណែកជួរដេកនីមួយៗហៅថា ឧទាហរណ៍ ឬ ករណី (example ឬ individual) ហើយជាវុិចទ័រដែលមានប្រវែង \(d\geq 1\) ៖ \[ x_i=\left(\begin{array} \ x_{i1} \\ x_{i2} \\ \vdots \\ x_{id} \end{array}\right)\in\mathbb{R}^d, i=1,...,n\ \text{។}\]

ក្នុងករណីនៃតម្រែតម្រង់តម្លៃ output \(y_i\) ទាំងអស់បង្ករបានជាវុិចទ័រដែលមានប្រវែង \(n\) តាងដោយ៖ \[ y=\left(\begin{array} \ y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{array}\right)\in\mathbb{R}^n\text{ ។}\] រាល់វុិចទ័រក្នុងការសិក្សានេះមានទម្រង់ជាជួរឈហើយអក្សរតូចនិង ធំ (small និង capital) មានន័យខុសគ្នា។

ក្នុងការសិក្សាសិក្ខាម៉ាសុីន ទិន្នន័យតាមជួរដេកទាំងអស់ត្រូវបានគេសន្មតថា មិនអាស្រ័យគ្នានិង មានរបាយដូចៗគ្នាពេលគេស្រង់យកវាមកពីសកល (independent and identically distributed ឬ iid) ហេតុនេះគេអាចនិយាយថាមានអថេរចៃដន្យ \((X,Y)\sim {\cal P}_{X,Y}\) ណាមួយដែលធម្មជាតិនៃការកើតឡើងរបស់វាដូចគ្នានឹងធម្មជាតិនៃទិន្នន័យ \((x_i,y_i)\) និងកំណត់សរសេរដោយ៖ \[(x_i,y_i)\sim (X,Y)\overset{iid}{\sim} {\cal P}_{X,Y},\ \forall i=1,...,n \text{ ។}\]

យើងមិនដាក់លក្ខខណ្ឌនៃភាពមិនអាស្រ័យគ្នារវាងអថេរនៃទិន្នន័យទេ (មានន័យថារវាងចំណោម \(X_j\) ទាំងអស់ និងរវាង \(Y\)) ដោយសារធម្មជាតិនៃអថេរទាំងអស់ត្រូវបានពណ៌នាយ៉ាងពេញលេញដោយ \({\cal P}_{X,Y}\) រួចទៅហើយ ។ ក្នុងកិច្ចការជាក់ស្តែងយើងមិនអាចស្គាល់ \({\cal P}_{X,Y}\) បានទេ ក៏ប៉ុន្តែដោយប្រើប្រាស់លក្ខណៈ \(iid\) នៃទិន្នន័យ រាល់តម្លៃទ្រឹស្តី (សង្ឃឹមមគណិត វ៉ារ្យង់ … ) ដែលទាក់ទងនឹងរបាយ \({\cal P}_{X,Y}\) អាចត្រូវបានប៉ាន់ស្មានដោយប្រើច្បាប់ប្រូបាបប៊ីលីតេ។ ការប៉ានស្មានរបាយទ្រឹស្តីដោយប្រើប្រាស់របាយទិន្នន័យត្រូវបានសិក្សាសុីជ្រៅក្នុងផ្នែកមួយដែលហៅថា ទ្រឹស្តីនៃ Empirical Process ហើយភាពរួមនៃរបាយទិន្នន័យទៅរករបាយទ្រឹស្តីត្រូវបានបកស្រាយនៅក្នុងទ្រឹស្តីបទដ៏ល្បីល្បាញមួយនៃស្ថិតិទ្រឹស្តីគឺ ទ្រឹស្តីបទ Vapnik Chervonenkis ។ ដោយសារទ្រឹស្តីទាំងនេះ ទាមទារបច្ចេកទេសផ្នែកទ្រឹស្តីសុីជម្រៅ ហេតុនេះយើងនឹងមិនសិក្សាពីវានៅក្នុងផ្នែកនេះទេ។ តែទោះជាយ៉ាងណាក៏ដោយ យើងគួរតែដឹងថា រាល់ការគណនាដោយប្រើប្រាស់ទិន្នន័យក្នុងការសិក្សាសិក្ខាម៉ាសុីន មានបាតគ្រឹះចេញពីទ្រឹស្តីស្ថិតិនិង ប្រូបាបប៊ីលីតេ។

៣. រង្វាស់នៃកំហុសនិង បរមាម៉ូដែល

ឥលូវយើងមានឧបរករណ៍គ្រប់គ្រាន់សម្រាប់ពណ៌នាពីសញ្ញាណដ៏សំខាន់នៃសិក្ខាម៉ាសុីនគឺ រង្វាស់នៃកំហុស (Loss) ។ ក្នុងការសិក្សាជាទូទៅចំពោះកិច្ចការបែបតម្រែតម្រង់តម្លៃ គេនិយមប្រើមធ្យមនៃលម្អៀងការ៉េ ឬ Mean Squared Error (MSE) ជារង្វាស់នៃកំហុសនិង កំណត់គុណភាពនៃម៉ូដែល។ ចំពោះម៉ូដែល \(f:\mathbb{R}^d\to\mathbb{R}\) ណាមួយដែលប្រើសម្រាប់ព្យាករណ៍តម្លៃនៃ output \(Y\) ផ្ទៀងផ្ទាត់ \(\mathbb{E}[|f(X)|^2]<+\infty\) គេកំណត់ MSE នៃ \(f\) ដោយ៖

\[ \text{MSE}(f)=\mathbb{E}_{X,Y}[(Y-f(X))^2] \tag{1}\]

ដែល \(\mathbb{E}_{X,Y}\) ជាតម្លៃមធ្យមតាមទ្រឹស្តីឬ សង្ឃឹមមគណិតធៀបនឹងរបាយនៃទិន្នន័យ \((X,Y)\) គឺ \({\cal P}_{X,Y}\)។ តើរង្វាស់ខាងលើមានន័យដូចម្តេច? វាជាតម្លៃមធ្យមនៃគម្លាតការ៉េរវាងអ្វីដែលព្យាករណ៍ដោយម៉ូដែល ពោលគឺ \(f(X)\) ទៅនឹងតម្លៃ output ពិតប្រាកដ \(Y\) ។ យើងថាម៉ូដែល \(f\) ល្អជាងម៉ូដែល \(g\) បើ \(\text{MSE}(f)<\text{MSE}(g)\) ។ នេះមានន័យថា ម៉ូដែលដែលល្អជាងគេគឺជាម៉ូដែលដែលមានតម្លៃ MSE អប្បរមា។

🤔 តើយើងគួរជ្រើសយកម៉ូដែល \(f\) បែបណាដើម្បីឲ្យ Equation 1 មានតម្លៃអប្បរមា?

បើយើងអាចឆ្លើយនឹងសំនួរនេះបាន នោះមានន័យថាយើងនឹងស្គាល់ម៉ូដែលល្អបំផុតសម្រាប់ធ្វើកិច្ចការបែបតម្រែតម្រង់តម្លៃដែលមាន MSE ជារង្វាស់នៃកំហុស។ ជារឿងល្អនោះគឺ យើងដឹងថាម៉ូដែលដែលល្អជាងគេនោះគឺ \(\eta:\mathbb{R}^d\to\mathbb{R}\) ដែលកំណត់ដោយ៖

\[\eta(x)=\mathbb{E}_{Y|X}(Y|X=x) \text{ ។} \tag{2}\]

យើងអាចស្រាយបានដោយងាយ (នៅផ្នែកចុងក្រោយនៃអត្ថបទ) ថា៖

\[ \begin{align} \text{MSE}(\eta)&=\min_{f\in{\cal M}}\text{MSE}(f)\\ &=\min_{f\in{\cal M}}\mathbb{E}_{X,Y}[(Y-f(X))^2] \end{align} \tag{3}\]

ដែល \({\cal M}=\{f:\mathbb{R}^d\to\mathbb{R},\mathbb{E}[|f(X)|^2]<+\infty\}\) ហើយសមភាពខាងលើមានន័យថា \(\eta\) ជាម៉ូដែលដែលផ្តល់តម្លៃ MSE តូចបំផុត។

ម៉ូដែល \(\eta\) ដែលកំណត់ក្នុង Equation 2 ខាងលើត្រូវបានហៅថា អនុគមន៍តម្រែតម្រង់តម្លៃ ឬ ការព្យាករណ៍បែប Bayes (regression function ឬ Bayes estimator) ។

រូបមន្តនៃបរមាម៉ូដែល \(\eta\) ខាងលើមានន័យថា តម្លៃព្យាករណ៍ \(\hat{y}=\eta(x)\) នៃ output របស់ \(x\) គឺជាតម្លៃមធ្យមឬ សង្ឃឹមគណិតមានលក្ខខណ្ឌ (conditional expectation) នៃអថេរចៃដន្យ \(Y\) ដោយដឹងថា input \(X\) យកតម្លៃស្មើនឹង \(x\) ។ យើងអាចគិតពីតម្លៃនេះតាមលំនាំដូចតទៅ៖ បើគេដឹងថា input \(X\) យកតម្លៃស្មើនឹង \(x\) ណាមួយ តើ output \(Y\) នៃ input ដទៃទៀតដែលស្រដៀងៗនឹង \(x\) មានតម្លៃជាមធ្យមប៉ុន្មាន? ពាក្យថា ស្រដៀងនឹង \(x\) ចង់សំដៅដល់របាយនៃទិន្នន័យក្រោមលក្ខខណ្ឌ \(X=x\) ហើយអ្វីដែលយើងចាប់អារម្មណ៍គឺតម្លៃមធ្យមនៃ output \(Y\) នៃទិន្នន័យទាំងនោះ។

🗝️ ជារួម រូបមន្ត \(\eta\) បញ្ជាក់ថាបើយើងចង់ព្យាករណ៍តម្លៃនៃវត្ថុណាមួយ យើងគួរពិនិត្យមើលតម្លៃនៃវត្ថុដែលមានលក្ខណៈប្រហាក់ប្រហែលនឹងវត្ថុនោះ។

🤔 បើយើងស្គាល់រូបមន្តម៉ូដែលល្អបំផុតទៅហើយ តើបញ្ហាតម្រែត្រង់តម្លៃនៅមានអ្វីជាភាពស្មុគស្មាញទៀត?

😣 ចម្លើយគឺព្រោះថា ក្នុងការងារជាក់ស្តែង យើងមិនអាចគណនា \(\eta\) បានទេដោយសារយើងមិនស្គាល់របាយនៃអថេរចៃដន្យមានលក្ខខណ្ឌ \(Y|X\) ។

នៅផ្នែកបន្តបន្ទាប់ទៀត យើងនឹងឃើញថាមានម៉ូដែលតម្រែតម្រង់តម្លៃជាច្រើនប្រភេទដែលសុទ្ធតែជាការប៉ាន់ស្មានតម្លៃនៃ \(\eta\) ពិសេសប្រភេទម៉ូដែលបែបអប៉ារ៉ាម៉ែត្រ (nonparametric models) ។

ឧទារហណ៍.១. ពិនិត្យមើលឧទាហរណ៍ខាងក្រោម៖

១. ដើម្បីព្យារករណ៍តម្លៃនៃផ្ទះមួយ យើងពិនិត្យមើលផ្ទះចំនួន \(K\) ដែលមានលក្ខណៈស្រដៀងនឹងវាបំផុតក្នុងចំណោមផ្ទះដែលមានទាំងអស់ (ស្រដៀងក្នុងន័យ input) ហើយគណនាតម្លៃមធ្យមនៃតម្លៃផ្ទះទាំងនោះ។ វិធីសាសស្រ្តបែបនេះហៅថា \(K\)-Nearest Neighbor (\(K\)NN) សម្រាប់តម្រែតម្រង់តម្លៃដែលជាវិធីសាស្រមួយដែលមានគោលដៅប៉ាន់ស្មានដោយផ្ទាល់ទៅលើតម្លៃនៃ \(\eta\) ។

២. បើយើងសន្មត់ថាបរមាម៉ូដែល \(\eta\) មានរាងជាអនុគមន៍លីនេអ៊ែរនៃ input នោះតម្លៃព្យាករណ៍ \(\hat{y}\) កំណត់ដោយ៖

\[\hat{y}=\beta_0+\beta_1X_1+\beta_2X_2+\dots+\beta_dX_d \tag{4}\]

ដែល \(\beta=(\beta_0,\beta_1,\dots,\beta_d)^t\in\mathbb{R}^{d+1}\) ជាមេគុណឬ ប៉ារ៉ាម៉ែត្រគន្លឹះនៃម៉ូដែលដែលយើងត្រូវកំណត់រក។ បញ្ហាប្រភេទនេះហៅថា តម្រែតម្រង់លីនេអ៊ែរ (linear regression) ដែលជាប្រភេទម៉ូដែលមូលដ្ឋានគ្រឹះដ៏សំខាន់និង ពេញនិយមមួយហើយក៏ជាប្រធានបទនៃអត្ថបទបន្ទាប់ផងដែរ។

៤. សង្ឃឹមគណិតមានលក្ខខណ្ឌនិង បរមាម៉ូដែល \(\eta\)

យើងនឹងបកស្រាយពីលទ្ធផលជាទ្រឹស្តីដែលបានបង្ហាញក្នុងផ្នែកមុន ជាពិសេសគឺ ភាពជាម៉ូដែលល្អបំផុតធៀបនឹង MSE នៃអនុគមន៍តម្រែតម្រង់តម្លៃ \(\eta\) កំណត់ក្នុង Equation 2 ។

៤.១. វុិចទ័រចៃដន្យ (Random vectors)

ដោយទិន្នន័យត្រូវបានប្រដូចនឹងឧបករណ៍គណិតវិទ្យាហៅថា អថេរនិង វុិចទ័រចៃដន្យ (random variable និង random vector) នោះយើងនឹងសិក្សានិយមន័យខ្លះៗនិងលក្ខណៈរបស់វុិចទ័រចៃដន្យពិសេសគឺ សង្ឃឹមគណិតមានលក្ខខណ្ឌដែលជានិយមន័យនៃបរមាម៉ូដែល \(\eta\) ។

និយមន័យ.១. បើ \(X=(X_1,...,X_d)\) ជាវុិចទ័រចៃដន្យមានអនុគមន៍ដង់សុីតេ \(f_X\) (ធៀបនឹងរង្វាស់ Lebesgue) កំណត់លើ \(\mathbb{R}^d\) នោះសង្ឃឹមគណិតនៃ \(X\) តាងដោយ \(\mu=\mathbb{E}(X)=(\mu_1, ..., \mu_d)\in\mathbb{R}^d\) ជាតម្លៃមធ្យមទ្រឹស្តីនៃ \(X\) កំណត់ដោយ៖ \[ \begin{align} \mu&=\int_{\mathbb{R}^d}xf_X(x)dx \end{align}\]

ខុសពីអថេរចៃដន្យមានមួយវិមាត្រ និយមន័យខាងលើមានន័យថា សង្ឃឹមគណិតនៃវុិចទ័រចៃដន្យមួយជាវុិចទ័រនៃសង្ឃឹមគណិតនៃកូអរដោនេររបស់វាគឺ \(\mu_j=\mathbb{E}(X_j)\) ចំពោះ \(j=1,...,d\) ។

លើសពីនេះទៅទៀតដើម្បីពណ៌នាពីភាពរាយប៉ាយនៃ \(X\) ក្នុងករណីវិមាត្រមួយគេប្រើប្រាស់ វ៉ារ្យង់ឬ គម្លាតស្តង់ដារ (variance ឬ standard deviation) តែក្នុងករណីនៃវុិចទ័រចៃដន្យយើងមិនត្រឹមតែត្រូវពណ៌នាពីកម្រិតនៃភាពរាយប៉ាយនៃ កូរអដោនេនីមួយៗរបស់វានោះទេ យើងត្រូវគិតពីទំនាក់ទំនងរវាងកូរអដោនេនីមួយៗរបស់វាថែមទៀងផង។ ទំនាក់ទំនងនិង កម្រិតរាយប៉ាយនេះត្រូវបានពណ៌នាដោយ ម៉ាទ្រីសកូវ៉ារ្យង់ កំណត់ដូចខាងក្រោម៖

និយមន័យ.២. ក្នុងករណីខាងលើ ម៉ាទ្រីសកូវ៉ារ្យង់នៃ \(X\) តាងដោយ \(\Sigma\in\mathbb{R}^{d\times d}\) កំណត់ដោយ៖ \[ \begin{align} \Sigma&=\mathbb{E}[(X-\mathbb{E}(X))(X-\mathbb{E}(X))^t]\\ &=\int_{\mathbb{R}^d}(x-\mu)(x-\mu)^tf_X(x)dx \end{align}\] ហើយយើងមាន៖ \[\begin{align} \Sigma_{ij}&=\mathbb{E}[(X_i-\mu_i)(X_j-\mu_j)] \end{align}\] ហៅថាកូវ៉ារ្យង់នៃកូអរដោនេ \(i\) និង \(j\) នៃវុិចទ័រចៃដន្យ \(X\) ហើយ ចំពោះ \(i=j\) យើងបានធាតុនៃអង្កត់ទ្រូង \(\Sigma_{jj}=\mathbb{V}(X_j)\) ជាវ៉ារ្យង់នៃកូអរដោនេទី \(j\) របស់វា។

អថេរចៃដន្យដែលមានសារៈសំខាន់និង ត្រូវបានប្រើប្រាស់ច្រើនជាងគេក្នុងការសិក្សាទិន្នន័យគឺ របាយណរម៉ាល់ឬ Gaussian (Normal ឬ Gaussian variable) ។ ក្នុងករណីវិមាត្រច្រើនជាង១ របាយនៃវុិចទ័រណរម៉ាល់នៅតែមានទម្រង់ល្អ (យើងអាចសរសេររូបមន្តនៃអនុគមន៍ដង់សុីតេ) និង មានសារៈសខាន់ជាខ្លាំងក្នុងការសិក្សានិង បង្ហាញពីទំនាក់ទំនងនៃកូអរដោនេរបស់វុិចទ័រចៃដន្យ។ ខាងក្រោមនេះជានិយមន័យនៃវុិចទ័រចៃដន្យណរម៉ាល់ក្នុងលំហវិមាត្រ \(d\geq 2\) ។

និយមន័យ.៣. \(X=(X_1,...,X_d)\) ហៅថា វុិចទ័រណរម៉ាល់ឬ វុិចទ័រ Guassian កាលណា គ្រប់បន្សំលីនេអ៊ែរនៃកូអរដោយនេរបស់វា ជាអថេរណរម៉ាល់ មានន័យថា \(\sum_{j=1}^d\alpha_jX_j\) ជាអថេរចៃដន្យណរម៉ាល់ចំពោះគ្រប់តម្លៃមេគុណ \(\alpha_j\in\mathbb{R}\) ដែល \(j=1,...,d\) ។ បើគេស្គាល់មធ្យម \(\mu\in\mathbb{R}^d\) និង ម៉ាទ្រីសកូវ៉ារ្យង់ \(\Sigma\in\mathbb{R}^{d\times d}\) នោះអនុគមន៍ដង់សុីតេរបស់វាកំណត់ដោយ៖ \[f_X(x)=\frac{1}{(2\pi)^{d/2}\sqrt{|\Sigma|}}e^{-\frac{1}{2}(x-\mu)^t\Sigma^{-1}(x-\mu)}\ \text{។}\] ក្នុងរូបមន្តខាងលើ \(|\Sigma|\) និង \(\Sigma^{-1}\) ជាដេទែមីណង់និង ចម្រាស់នៃ \(\Sigma\) រាងគ្នា។ គេកំណត់តាងវុិចទ័រណរម៉ាល់ដែលមានមធ្យម \(\mu\) និង ម៉ាទ្រីសកូវ៉ារ្យង់ \(\Sigma\) ដោយ \(X\sim{\cal N}(\mu, \Sigma)\) ។

ឧទាហរណ៍.២. ខាងក្រោមយើងមានចំណុចចំនួន \(n\) នៃវុិចទ័រណរម៉ាល់ក្នុងប្លង់ដែលកំណត់ដោយមធ្យមនិង ម៉ាទ្រីសកូវ៉ារ្យង់ផ្សេងៗគ្នាតាមករណីនីមួយៗ៖

១. \(n=200, X\sim{\cal N}\left(\left(\begin{array}\ 0 \\ 0\end{array}\right), \left(\begin{array}\ 1 & 0\\ 0 & 2\end{array}\right)\right)\)

២. \(n=200, X\sim{\cal N}\left(\left(\begin{array}\ 5 \\ 5\end{array}\right), \left(\begin{array}\ 2 & -1\\ -1 & 2\end{array}\right)\right)\)

៣. \(n=200, X\sim{\cal N}\left(\left(\begin{array}\ -1 \\ 6\end{array}\right), \left(\begin{array}\ 2 & 1.2\\ 1.2 & 1\end{array}\right)\right)\)

៤. \(n=200, X\sim{\cal N}\left(\left(\begin{array}\ 6 \\ 0\end{array}\right), \left(\begin{array}\ 3 & 0.1\\ 0.1 & 0.25\end{array}\right)\right)\)

Code

import numpy as np
import plotly.graph_objs as go
mu1, Sigma1 = [0, 0], [[1, 0], [0, 3]]

mu2, Sigma2  = [5, 5], [[2, -1], [-1, 2]]

mu3, Sigma3 = [-1, 6], [[2, 1.2], [1.2, 1]]

mu4, Sigma4 = [6, 0], [[3, 0.1], [0.1, 0.25]]
x1 = np.random.multivariate_normal(mean=mu1, cov=Sigma1, size=100)
x2 = np.random.multivariate_normal(mean=mu2, cov=Sigma2, size=100)
x3 = np.random.multivariate_normal(mean=mu3, cov=Sigma3, size=100)
x4 = np.random.multivariate_normal(mean=mu4, cov=Sigma4, size=100)
fig = go.Figure(
    go.Scatter(x=x1[:,0], y = x1[:,1],
               mode = "markers",
               name = "ករណីទី១",
               showlegend = True,
               marker = dict(size = 10)))
fig.add_trace(
    go.Scatter(x=x2[:,0], y = x2[:,1],
               mode = "markers",
               name = "ករណីទី២",
               showlegend = True,
               marker = dict(size = 10)))
fig.add_trace(
    go.Scatter(x=x3[:,0], y = x3[:,1],
               mode = "markers",
               name = "ករណីទី៣",
               showlegend = True,
               marker = dict(size = 10)))
fig.add_trace(
    go.Scatter(x=x4[:,0], y = x4[:,1],
               mode = "markers",
               name = "ករណីទី៤",
               showlegend = True,
               marker = dict(size = 10)))
fig.update_layout(title = "វុិចទ័រណរម៉ាល់វិមាត្រ២",
                  width = 600,
                  height = 600)
fig.show()

រូបទី២៖ របាយនៃវុិចទ័រណរម៉ាល់២វិមាត្រអាស្រ័យទៅតាមមធ្យមនិង ម៉ាទ្រីសកូវ៉ារ្យង់របស់វា។

ក្នុងឧទាហរណ៍ខាងលើ របាយចំណុចក្នុងក្រុមនីមួយៗនៅរាយប៉ាយព័ទ្ធជុំវិញមធ្យម \(\mu\) ហើយទ្រង់ទ្រាយនៃរបាយចំណុចអាស្រ័យនឹងម៉ាទ្រីសកូវ៉ារ្យង់របស់វា។ បើយើងសង្កេតមើលក្រុមទី២ (ពណ៌ក្រហម) របាយចំណុចនៅរាយប៉ាយជុំវិញមធ្យមរបស់វាគឺ \(\mu=\left(\begin{array}\ 5\\5\end{array}\right)\) ហើយបើនិយាយពីទ្រង់ទ្រាយនៃចំណុចវិញ ពេលដែលតម្លៃលើអ័ក្ស \(x\) កើនយើងឃើញថាតម្លៃលើអ័ក្ស \(y\) មានទំនោរធ្លាក់ចុះដោយសារម៉ាទ្រីសកូវ៉ារ្យង់របស់វាមានកូវ៉ារ្យង់អវិជ្ជមានស្មើនឹង \(-1\) (ធាតុលើអង្កត់ទ្រូងច្រាស់នៃម៉ាទ្រីសកូវ៉ារ្យង់) ហើយកម្រិតនៃការរាយប៉ាយតាមទិស \(x\) និង \(y\) មានតម្លៃប្រហែលគ្នាដោយសារវ៉ារ្យង់នៃកូអរដោនេទាំងពីរមានតម្លៃស្មើគ្នាស្មើនឹង \(2\) (ធាតុនៃអង្កត់ទ្រូងនៃម៉ាទ្រីសកូវ៉ារ្យង់) ។

៤.២. សង្ឃឹមគណិតមានលក្ខខណ្ឌ (conditional expectation)

ចំពោះវុិចទ័រចៃដន្យជាប់ (continuous random vector) ដើម្បីយល់ពីសង្ឃឹមគណិតមានលក្ខខណ្ឌយើងត្រូវស្គាល់ដង់សុីតេមានលក្ខខណ្ឌជាមុនសិន។

និយមន័យ.៤. បើ \((X,Y)\) ជាវុិចទ័រចៃដន្យរួមនៃវុិចទ័រចៃដន្យ \(X\) និង \(Y\) កំណត់លើ \(\mathbb{R}^{d_1}\) និង \(\mathbb{R}^{d_2}\) រាងគ្នាហើយមានដង់សុីតេរួម (joint density) \(f_{X,Y}\) នោះដង់សុីតេមានលក្ខខណ្ឌនៃ \(Y\) ដោយដឹងថា \(X=x\in\mathbb{R}^{d_1}\) កំណត់តែចំពោះ \(x\) ដែល \(f_X(x)>0\) ដោយ៖ \[f_{Y|X}(y|X=x)=\frac{f_{X,Y}(x,y)}{f_{X}(x)}\] ដែល \(f_X(x)=\int_{\mathbb{R}^{d_2}}f_{X,Y}(x,y)dy\) ហៅថាដង់សុីតេដោយផ្នែក (marginal density) នៃ \(X\) ចេញពីដង់សុីតេរួម \(f_{X,Y}\) ។

ឧទាហរណ៍.៣. តាង \(\mathbb{R}^*=\mathbb{R}\setminus \{0\}\) និង \(\Omega=(\mathbb{R}^*)^2\times[0,1]\) ។ គណនាដង់សុីតេមានលក្ខខណ្ឌ \(f_{Y|X}(y|X=x)\) ចំពោះ \(x\neq(0,0)\) ដោយដឹងថា \[f_{X,Y}(x,y)=\begin{cases}Cye^{-\|x\|^2y}, & (x,y)\in \Omega\\ 0, &(x,y)\notin \Omega\end{cases}\] ចំពោះចំនួនពិត \(C>0\) ។

Code

import plotly.graph_objects as go
C = 1/np.pi
def f_XY(x,y):
  return C * y * np.exp(-np.dot(x,x)*y)
N = 30
def grid(y):
  x = np.linspace(-3,3,N)
  X = np.array([[i,j] for i in x for j in x])
  for i in range(len(y)):
    if i == 0:
      res = np.column_stack([X, [f_XY(X[j], y[i]) for j in range(X.shape[0])]])
    else:
      Y = np.column_stack([X, [f_XY(X[j], y[i]) for j in range(X.shape[0])]])
      res = np.row_stack([res, Y])
  return res

y = np.linspace(0,1,5)
data = grid(y)
layout = go.Layout(
    title = 'ដង់សុីតេរួមនៃចំពោះតម្លៃខ្លះៗនៃ y',
    width = 650,
    height = 400
)
fig = go.Figure(layout=layout)
frames = []
start, end = 0, 900
x_, y_ = np.linspace(-3,3,N), np.linspace(-3,3,N)
op = [1-0.15*i for i in range(1, 6)]
# col = ['Viridis', 'RdBu', 'Inferno', 'Bluered_r', 'Cividis_r']
for i in range(len(y)):
    id = range(start, end)
    z = data[id,-1].reshape(N,N)
    trace = go.Surface(
        z=z,
        x=x_,
        y=y_,
        colorbar_x = -0.01,
        opacity=op[i],
        name = 'y = {}'.format(np.round(y[i],3)),
        showlegend = True,
        colorscale= 'RdBu',
        colorbar=dict(title="ដង់សុីតេ"),
        cmin=0,
        cmax=0.325
    )
    fig.add_trace(trace)
    start, end = end, end + 900
fig.update_layout(scene = dict(xaxis_title = 'x1',
                  yaxis_title ='x2',
                  zaxis_title='f_(x1,x2,y)'))
fig.show()

រូបទី៣៖ ដង់សុីតេរួម \(f_{X,Y}\) ចំពោះតម្លៃខ្លះៗនៃ \(y\) ។

ជាដំបូងយើងកំណត់ \(C\) ដោយប្រើលក្ខណៈនៃអនុគមន៍ដង់សុីតេ \(\int_{\Omega}f_{X,Y}(x,y)dxdy=1\) ហើយដោយបម្លែងអាំងតេក្រាលធៀប \(x\) ជាទម្រង់ប៉ូលែរ គេបាន៖ \[ \begin{align} 1&=C\int_{\Omega}ye^{-\|x\|^2y}dxdy\\ &=C\int_0^{+\infty}\int_0^{+\infty}\int_0^{2\pi}yre^{-r^2y}drd\theta dy\\ &=\pi C\int_0^1\int_0^{+\infty}e^{-u}dudy,\ \ (u=r^2y)\\ &=\pi C\int_0^1dy\\ \Rightarrow C&=1/\pi \end{align} \]
យើងគណនាដង់សុីតេដោយផ្នែកនៃ \(X\) ចំពោះ \(x\neq (0,0)\) ដោយអាំងតេក្រាលធៀបនឹង \(Y\) ៖ \[ \begin{align} f_{X}(x)&=\int_0^1 f_{X,Y}(x,y)dy\\ &=-\frac{1}{\pi\|x\|^2}\int_0^1yd(e^{-\|x\|^2y})\\ &=-\frac{1}{\pi\|x\|^2}\left[e^{-\|x\|^2}-\int_0^1e^{-\|x\|^2y}dy\right]\\ &=-\frac{1}{\pi\|x\|^2}\left[e^{-\|x\|^2}+\frac{1}{\|x\|^2}e^{-\|x\|^2y}\Big|_0^1\right]\\ &=\frac{1}{\pi\|x\|^4}\left[1-(1+\|x\|^2)e^{-\|x\|^2}\right] \end{align} \]
ចុងក្រោយ យើងគណនាដង់សុីតេមានលក្ខខណ្ឌតាមនិយមន័យ៖

\[ \begin{align} f_{Y|X}(y|X=x)&=\frac{f_{X,Y}(x,y)}{f_{X}(x)}\\ &=\frac{\frac{1}{\pi}ye^{-\|x\|^2y}}{\frac{1}{\pi\|x\|^4}\left[1-(1+\|x\|^2)e^{-\|x\|^2}\right]}\\ &=\frac{e^{\|x\|^2(1-y)}y\|x\|^4}{e^{\|x\|^2}-\|x\|^2-1} \qquad \blacksquare \end{align} \]

ក្នុងចម្លើយចុងក្រោយនៃដង់សុីតេមានលក្ខខណ្ឌនេះ \(x\) ត្រូវបានចាត់ទុកជាចំនួនថេរហើយអញ្ញាតរបស់វាគឺ \(y\in[0,1]\) ។

ឥលូវនេះយើងអាចនិយាយពីចំណុចសំខាន់នៃការសិក្សាផ្នែកទ្រឹស្តីនៃតម្រែតម្រង់តម្លៃគឺ សង្ឃឹមគណិតមានលក្ខខណ្ឌ។

និយមន័យ.៥. បើ \((X,Y)\) ជាវុិចទ័រចៃដន្យរួមនៃវុិចទ័រចៃដន្យ \(X\) និង \(Y\) កំណត់លើ \(\mathbb{R}^{d_1}\) និង \(\mathbb{R}^{d_2}\) រាងគ្នា ហើយមានដង់សុីតេមានលក្ខខណ្ឌ \(f_{Y|X}\) នៃ \(Y|X\) នោះសង្ឃឹមគណិតមានលក្ខខណ្ឌនៃ \(Y\) ដោយដឹងថា \(X=x\in\mathbb{R}^{d_1}\) កំណត់ដោយ៖ \[\mathbb{E}(Y|X=x)=\int_{\mathbb{R}^{d_2}}yf_{Y|X}(y|X=x)dy\] ដែលជាអនុគមន៍នៃ \(x\) ។

ឧទាហរណ៍.៤. ចំពោះ ឧទាហរណ៍.៣. ខាងលើ យើងអាចគណនា \(\mathbb{E}(Y|X=x)\) ដោយ៖

\[ \begin{align} \mathbb{E}(Y|X=x)&=\int_0^1yf_{Y|X}(y|X=x)dy\\ &=\frac{\|x\|^4e^{\|x\|^2}}{e^{\|x\|^2}-\|x\|^2-1}\int_0^1y^2e^{-\|x\|^2y}dy\\ &=\frac{\|x\|^4e^{\|x\|^2}}{e^{\|x\|^2}-\|x\|^2-1}\left[-e^{-\|x\|^2y}\left(\frac{y^2}{\|x\|^2}+\frac{2y}{\|x\|^4}+\frac{2}{\|x\|^6}\right)\right]_0^1\\ &=\frac{\|x\|^4e^{\|x\|^2}}{e^{\|x\|^2}-\|x\|^2-1}\left[\frac{2}{\|x\|^6}-e^{-\|x\|^2}\left(\frac{1}{\|x\|^2}+\frac{2}{\|x\|^4}+\frac{2}{\|x\|^6}\right)\right]\\ &=\frac{2(e^{\|x\|^2}-\|x\|^2-1)-\|x\|^4}{(e^{\|x\|^2}-\|x\|^2-1)\|x\|^2}\qquad \blacksquare \end{align} \]

ប្រសិនបើយើងឧបមាថាទិន្នន័យ \((X,Y)\in \Omega\) មានរបាយកំណត់ ក្នុងឧទាហរណ៍.៣. ខាងលើ នោះយើងនឹងអាចគណនារូបមន្តសម្រាប់ព្យាករណ៍ \(Y\) ដែលល្អជាងគេសម្រាប់រង្វាស់កំហុស MSE កំណត់ដោយ៖ \[\hat{y}=\frac{2(e^{\|x\|^2}-\|x\|^2-1)-\|x\|^4}{(e^{\|x\|^2}-\|x\|^2-1)\|x\|^2}\text{ ។}\]

Code

# របាយដោយផ្នែកធៀប X
def f_Y_known_X(x):
  norm_x = np.dot(x,x)
  return (np.exp(norm_x*(1-y))*y*norm_x ** 2)/ (np.exp(norm_x)-norm_x-1)

def eta(x):
  return (2*(np.exp(x)-x-1)-x**2) / ((np.exp(x)-x-1)*x)

x = np.linspace(0.001, 100, 200)
y = eta(x)
fig = go.Figure([go.Scatter(x = x,
                            y = y,
                            mode = 'lines',
                            name = "បរមាម៉ូដែល",
                            showlegend = True)])
fig.update_layout(title = "បរមាម៉ូដែលជាអនុគន៍នៃការ៉េរបស់ណម x",
                  width = 600, height = 400,
                  xaxis_title= "||x||^2",
                  yaxis_title="តម្លៃ output")
fig.show()

រូបទី៤៖ បរមាម៉ូដែលក្នុង ឧទាហរណ៍.៤. ជាអនុគន៍នៃ \(x\) ។

ជាពិសេសដោយប្រើពន្លាតជាស៊េរីពិតនៃអនុគមន៍អ៊ិស៉្បូណង់ស្យែល \(e^{t}=1+t+t^2/2+...=\sum_{k=0}^{+\infty}\frac{t^k}{k!}\) នោះកន្សោមនៃការព្យាករណ៍ខាងលើសមមូលនឹង \(\frac{\|x\|^6/3+o(\|x\|^6)}{\|x\|^6/2+o(\|x\|^6)}\) ពេល \(\|x\|\to 0\) ដូច្នេះ យើងអាចព្យាករណ៍តម្លៃ \(Y\) ត្រង់ \(X=(0,0)\) តាមបន្លាយភាពជាប់គឺ \(\hat{y}(0,0)=\mathbb{E}(Y|X=(0,0))=2/3\) ។

ឥលូវយើងសាកស្រង់ទិន្នន័យចេញពីរបាយប្រូបាបប៊ីលីតេខាងលើនិង ផ្ទៀតផ្ទាត់មើលថាតើម៉ូដែលដែលយើងបានគណនាពិតជាមានសមត្ថភាពក្នុងការព្យាករណ៍បានល្អឬ យ៉ាងណា?

Code

def f_nX_Y(x,y):
  return y*np.exp(-x*y)

def d_cauchy(x):
  return 1/(1+x)

# បង្កើតទិន្នន័យតាម វិធីសាស្រ Rejection sampling
res = []
while len(res) < 100:
  n_x = np.tan(np.pi*(np.random.uniform(0,1) - 1/2)) ** 2
  n_y = np.random.uniform(0,1)
  if np.random.uniform(0,1) <=  f_nX_Y(n_x, n_y) / d_cauchy(n_x):
    if len(res) < 80:
      res.append([n_x, n_y])
    if len(res) >= 80:
      if n_x >= 10:
        res.append([n_x, n_y])

res = np.array(res)
y_mod = eta(res[:,0])
fig = go.Figure([go.Scatter(x = res[:,0],
                            y = y_mod,
                            mode = 'markers',
                            name = "បរមាម៉ូដែល",
                            showlegend = True)])
fig.add_trace(go.Scatter(x = res[:,0],
                         y = res[:,1],
                         mode = 'markers',
                         name = "ទិន្នន័យដែលស្រង់ពីរបាយប្រូបាប",
                         showlegend = True,
                         marker = dict(color = "red")))
fig.update_layout(title = "បរមាម៉ូដែលនិង ទិន្នន័យស្រង់ពីរបាយប្រូបាបជាអនុគន៍នៃការ៉េរបស់ណម x",
                  width = 650, height = 400,
                  xaxis_title='||x||^2',
                  yaxis_title="តម្លៃ ouput")
mse = np.mean((res[:,1] - y_mod ** 2))
fig.add_annotation(
  x=np.max(res[:,0])/2, 
  y=np.mean(y_mod),
  text="MSE = {}".format(np.round(mse, 3)),
  showarrow=False,
  arrowhead=1)
fig.show()

រូបទី៥៖ ទិន្នន័យតាមរបាយប្រូបាប (ដោយប្រើវិធីសាស្រ្ត Rejection sampling) និង ការព្យាករណ៍ដោយបរមាម៉ូដែល ។ យើងឃើញថាការព្យារកណ៍កាន់តែសុក្រិតនៅពេលណម \(X\) យកតម្លៃកាន់តែធំ នេះក៏ព្រោះតែកាលណាណម \(X\) មានតម្លៃធំ ដង់សុីតេរួមមានតម្លៃសឹងតែសូន្យគ្រប់ទីកន្លែងទៅហើយ លើកលែងតែចំពោះ \(Y\) នៅក្បែរៗនឹង \(0\) ប៉ុណ្ណោះ។ ក្នុងករណីនេះ ទាំងទិន្នន័យដែលបង្កើតតាមរបាយប្រូបាបរួមនិង ម៉ូដែលសុទ្ធប្រើប្រាស់តម្លៃ \(Y\) ប្រហាក់ប្រហែលគ្នា ដែលធ្វើឲ្យម៉ូដែលព្យាករណ៍បានល្អ។

ផ្នែកលក្ខខណ្ឌនៃសង្ឃឹមគណិតមានលក្ខខណ្ឌអាចជាវត្ថុគណិតវិទ្យាផ្សេងក្រៅពី វុិចទ័រចៃដន្យ។ ខាងក្រោមនេះជានិយមនៃសង្ឃឹមគណិតមានលក្ខខណ្ឌធៀបនឹង \(\sigma\) ពីជគណិតមួយ មួយ។

និយមន័យ.៦. បើ \(\cal F\) ជា \(\sigma\) ពីជគណិតរងនៃ \(\sigma\) ពីជគណិតបង្ករដោយ \({Y}\) តាងដោយ \(\sigma(Y)\) នោះគេមានសង្ឃឹមគណិតមានលក្ខខណ្ឌធៀបនឹង (ឬ ដោយដឹងពត៌មានកំណត់ដោយ \(\sigma\) ពីជគណិត) \(\cal F\) តាងដោយ \(\mathbb{E}(Y|{\cal F})\) តែមួយគត់ដែលជាអថេរចៃដន្យវាស់បានធៀបនឹង \({\cal F}\) ផ្ទៀតផ្ទាត់៖ \[\mathbb{E}[\mathbb{1}_{\{A\}}\mathbb{E}(Y|{\cal F})]=\mathbb{E}[\mathbb{1}_{\{A\}}Y]\] ចំពោះគ្រប់ព្រឹត្តិការណ៍ \(A\in{\cal F}\) ។ ជាសម្គាល់៖
១. \(\mathbb{1}_{\{A\}}\) ជាអនុគមន៍សម្គាល់នៃ \(A\) ដែល \(\mathbb{1}_{\{A\}}(\omega)=1\) បើ \(\omega\in A\) និង \(\mathbb{1}_{\{A\}}(\omega)=0\) បើ \(\omega\notin A\)។
២. \(\mathbb{E}(Y|X)=\mathbb{E}(Y|\sigma(X))\) ។

នេះមានន័យថា \(\mathbb{E}(Y|{\cal F})\) ជាអថេរចៃដន្យវាស់បានធៀបនឹង \({\cal F}\) ដែលសង្ឃឹមគណិតនៃបង្រួមរបស់វាលើគ្រប់ព្រឹត្តិការណ៍ \(A\) ត្រួតសុីគ្នានឹងសង្ឃឹមគណិតនៃបង្រួមរបស់ \(X\) ទៅលើព្រឹត្តិការណ៍ដូចគ្នា ចំពោះគ្រប់ \(A\in{\cal F}\) ទាំងអស់។

សង្ឃឹមគណិតមានលក្ខខណ្ឌក៏ដូចជាសង្ឃឹមគណិតគ្មានលក្ខខណ្ឌដែរ ហេតុនេះវាផ្ទៀងផ្ទាត់លក្ខណៈទាំងឡាយនៃសង្ឃឹមគណិតទូទៅដូចជាលក្ខណៈលីនេអ៊ែរនិង លក្ខណៈម៉ូណូតូនជាដើម។ ខាងក្រោមជាលក្ខណៈពិសេសមួយសម្រាប់ឲ្យយើងស្រាយពីលក្ខណៈបរមានៃ បរមាម៉ូដែល \(\eta\) នៅក្នុងកិច្ចការបែបតម្រែតម្រង់តម្លៃមាន MSE ជារង្វាស់នៃកំហុស។

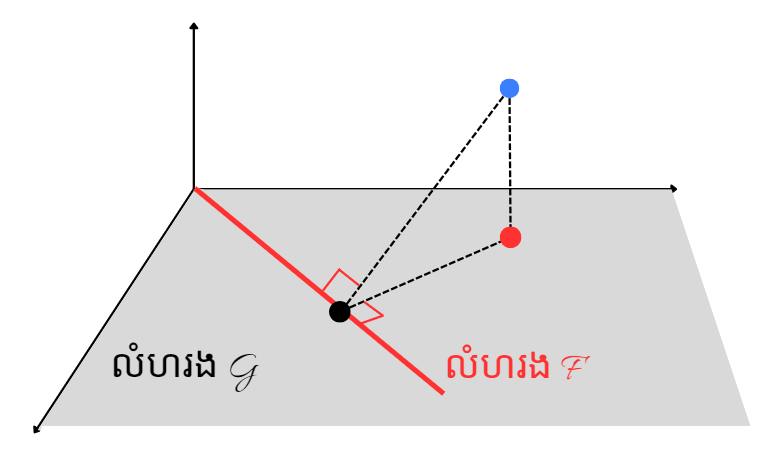
លក្ខណៈ Tower នៃសង្ឃឹមគណិតមានលក្ខខណ្ឌ៖ បើ \({\cal F}\subset{\cal G}\subset \sigma(X)\) ជា \(\sigma\) ពីជគណិតរងពីរនៃ \(\sigma(X)\) នោះយើងបាន៖ \[\mathbb{E}[\mathbb{E}(X|{\cal G})|{\cal F}]=\mathbb{E}(X|{\cal F})\ \text{។}\]

លក្ខណៈ Tower មានន័យថាការគណនាសង្ឃឹមគណិតធៀបនឹងលំហរធំសិន រួចហើយបន្តគណនាធៀបនឹងលំហតូចមានតម្លៃស្មើនឹងសង្ឃឹមគណិតមានលក្ខខណ្ឌធៀបនឹងលំហតូចតែម្តង។ នេះប្រៀបដូចជាការធ្វើចំណោលកែងចំណុចពីលើលំហធំទៅលើលំហតូចដែរ។

រូបទី៦. លក្ខណៈ Tower នៃសង្ឃឹមគណិតមានលក្ខខណ្ឌអាចប្រដូចនឹងចំណោលកែងក្នុងរូបខាងលើ។ ចំណុចពណ៌ខៀវតាងឲ្យ \(X\) ហើយចំណុចក្រហមជាសង្ឃឹមគណិតមានលក្ខខណ្ឌធៀបនឹង \(\cal G\) (ប្លង់) គឺ \(\mathbb{E}(X|{\cal G})\) និង ចំណុចពណ៌ខ្មៅជាសង្ឃឹមគណិតមានលក្ខខណ្ឌធៀបនឹង \(\cal F\) (បន្ទាត់) គឺ \(\mathbb{E}(X|{\cal F})\) ។ ការធ្វើចំំណោលកែងពីចំណុចខៀវគឺ \(X\) ទៅលើ \(\cal G\) ដោយឲ្យជាចំណុចក្រហមគឺ \(\mathbb{E}(X|{\cal G})\) រួចបន្តធ្វើចំណោលទៅលើ \(\cal F\) ដោយឲ្យជា \(\mathbb{E}[\mathbb{E}(X|{\cal G})|{\cal F}]\) គឺដូចនឹងការធ្វើចំណោលពី \(X\) ទៅលើ \(\cal F\) ដោយឲ្យជា \(\mathbb{E}(X|{\cal F})\) តែម្តង។

ឧទាហរណ៍.៥. តាមលក្ខណៈខាងលើគេបាន៖

១. \(\mathbb{E}(Y|{\cal F})=Y\) បើ \(Y\) វាស់បានធៀបនឹង \({\cal F}\) ។ ជាពិសេស \(\mathbb{E}(f(X)|X)=f(X)\) ចំពោះគ្រប់អនុគមន៍ \(f\) ដែលសង្ឃឹមគណិតរបស់វាអាចកំណត់បាន (ព្រោះ \(X\) វាស់បានធៀបនឹង \(\sigma(X)\)) ។

២. \(\mathbb{E}(Y|{\cal F})=\mathbb{E}(Y)\) លុះត្រាតែ \(Y\) មិនអាស្រ័យនឹង \({\cal F}\) ដែលកំណត់តាងដោយ \(Y{\perp\!\!\!\!\perp} {\cal F}\) ។

៣. \(\mathbb{E}[\mathbb{E}(Y|{\cal F})]=\mathbb{E}(Y)\) ព្រោះបើយើងតាងលំហសំណាក់ដោយ \(\Omega\) នោះតាមនិយមនន័យនៃសង្ឃឹមគណិតមានលក្ខខណ្ឌគេបាន៖ \[ \begin{align} \mathbb{E}(Y)&=\mathbb{E}[\mathbb{1}_{\{\Omega\}}Y]\\ &=\mathbb{E}[\mathbb{1}_{\{\Omega\}}\mathbb{E}(Y|{\cal F})],\qquad(\Omega\in{\cal F})\\ &=\mathbb{E}[\mathbb{E}(Y|{\cal F})],\qquad(\mathbb{1}_{\{\Omega\}}=1) \end{align} \]

ចុងក្រោយបំផុតនៃផ្នែកនេះ យើងនឹងស្រាយបរមាភាពនៃ \(\eta\) នៃសមីការ Equation 3 ។ ចំពោះ \(f\) ទូទៅធាតុនៃ \(\cal M\) គេបាន៖ \[ \begin{align} \text{MSE}(f)&=\mathbb{E}[(Y-f(X))^2]\\ &=\mathbb{E}[(Y-\eta(X)+\eta(X)-f(X))^2]\\ &=\mathbb{E}[(Y-\eta(X))^2]+2\mathbb{E}[(Y-\eta(X))(\eta(X)-f(X))]+\mathbb{E}[(\eta(X)-f(X))^2] \end{align} \] ដោយពិនិត្យតួរកណ្តាលនៃកន្សោមខាងលើនិងប្រើលក្ខណៈសង្ឃឹមគណិតមានលក្ខខណ្ឌ យើងបាន៖ \[ \begin{align} \mathbb{E}[(Y-\eta(X))(\eta(X)-f(X))]&=\mathbb{E}[\mathbb{E}[(Y-\eta(X))(\eta(X)-f(X))|X]]\\ &=\mathbb{E}[(\eta(X)-f(X))\mathbb{E}[(Y-\eta(X))|X]]\\ &=\mathbb{E}[(\eta(X)-f(X))(\underbrace{\mathbb{E}(Y|X)-\eta(X)}_{0})]\\ &=0 \end{align} \] ដែលបន្ទាត់ទីពីរពិតយោងទៅតាមលក្ខណៈទី១ នៃ ឧទាហរណ៍.៥. ខាងលើ។ ហេតុនេះយើងបាន៖ \[ \begin{align} \text{MSE}(f)&=\mathbb{E}[(Y-\eta(X))^2]+\mathbb{E}[(\eta(X)-f(X))^2]\\ &\geq\mathbb{E}[(Y-\eta(X))^2],\qquad (\mathbb{E}[(\eta(X)-f(X))^2]\geq 0)\\ &=\text{MSE}(\eta) \end{align} \] បញ្ហាត្រូវបានស្រាយបញ្ជាក់ដោយសារ \(\eta\in{\cal M}\) ។ \(\blacksquare\)

🗝️ អត្ថន័យសំខាន់នៃទ្រឹស្តីខាងលើគឺមានន័យថា \(\eta(X)=\mathbb{E}(Y|X)\) ជាចំណោលកែងនៃ \(Y\) ទៅលើលំហនៃពត៌មានដែលបង្ករដោយ \(X\) ព្រោះថា \(\eta(X)\) ជាអនុគមន៍នៃ \(X\) ដែលមានចម្ងាយទៅ \(Y\) ខ្លីបំផុត (ចំពោះចម្ងាយ \(d(X,Y)=(\mathbb{E}[(X-Y)^2])^{(1/2)}, X,Y\in\mathbb{R}\)) ។