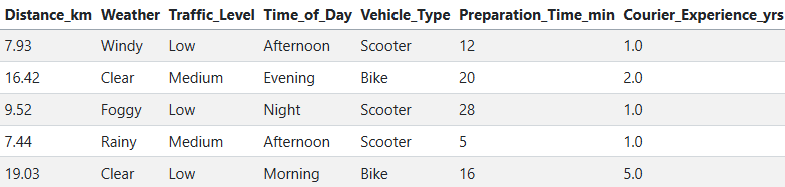
Code
| country | continent | lifeExp | pop | gdpPercap |
|---|---|---|---|---|
| Afghanistan | Asia | 43.828000 | 31889923 | 974.580338 |
| Albania | Europe | 76.423000 | 3600523 | 5937.029526 |
| Algeria | Africa | 72.301000 | 33333216 | 6223.367465 |
| Angola | Africa | 42.731000 | 12420476 | 4797.231267 |
| Argentina | Americas | 75.320000 | 40301927 | 12779.379640 |