![]() Content
Content
Introduction & Brief History
World of Approximation
Neural Networks
Optimization
Applications
Introduction & Brief History
World of Approximation
Neural Networks
Optimization
Applications
Deep Learning (DL) is a subset of Machine Learning (ML) that uses Multilayer Neural Networks, called Deep Neural Networks (DNN), to simulate the complex decision-making power of the human brain 🧠. Some form of deep learning powers most of the Artificial Intelligence (AI) applications in our lives today.
Year |
Development |
|---|---|
| 1943 | Walter Pitts and Warren McCulloch created the first computer model based on neural networks, using “threshold logic” to mimic the thought process. |
| 1960s | Henry J. Kelley developed the basics of a continuous backpropagation model, and Stuart Dreyfus simplified it using the chain rule. |
| 1965 | Alexey Ivakhnenko and Valentin Lapa developed early deep learning algorithms using polynomial activation functions. |
| 1980s | Geoffrey Hinton1 and colleagues revived neural networks by demonstrating effective training using backpropagation |
| 1970s | The first AI winter occurred due to unmet expectations, leading to reduced funding and research. |
| 1980s | Despite the AI winter, research continued, leading to significant advancements in neural networks and deep learning. |
| 1990s | Development of convolutional neural networks (CNNs) by Yann LeCun and others for image recognition. |
| 2006 | Geoffrey Hinton and colleagues introduced deep belief networks, which further advanced deep learning techniques. |
| 2012 | AlexNet, a deep convolutional neural network, won the ImageNet competition, showcasing the power of deep learning in computer vision. |
| 2016 | AlphaGo by DeepMind defeated a human Go champion, demonstrating the potential of deep learning in complex games. |
| Present | Deep learning continues to evolve, with applications in natural language processing, speech recognition, autonomous vehicles, and more. |
Year |
Key Model Development |
|---|---|
| 1943 | Pitts and McCulloch’s neural network model. |
| 1960s | Kelley’s backpropagation model and Dreyfus’s chain rule simplification. |
| 1980s | Hinton’s backpropagation revival & Recurrent Neural Networks (RNNs). |
| 1990s | LeCun’s Convolutional Neural Networks (CNNs). |
| 2006 | Deep belief networks. |
| 2012 | AlexNet’s ImageNet win. |
| 2016 | AlphaGo’s victory. |
| 2017 | Attention is all you need (key models of ChatGPT) |
Approximation is the process of finding a value that is close to the true value of a quantity, but not exactly equal to it. It is often used when an exact value is difficult to obtain or not necessary.Interest Per Year |
N Compound |
Total |
|---|---|---|
| \(100\%\) | 1 | \(1+1\) |
| \(100\%\) | 2 | \((1+1/2)^2\) |
| \(100\%\) | 3 | \((1+1/3)^3\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(100\%\) | n | \((1+1/n)^n\) |
ads) and targets (sales).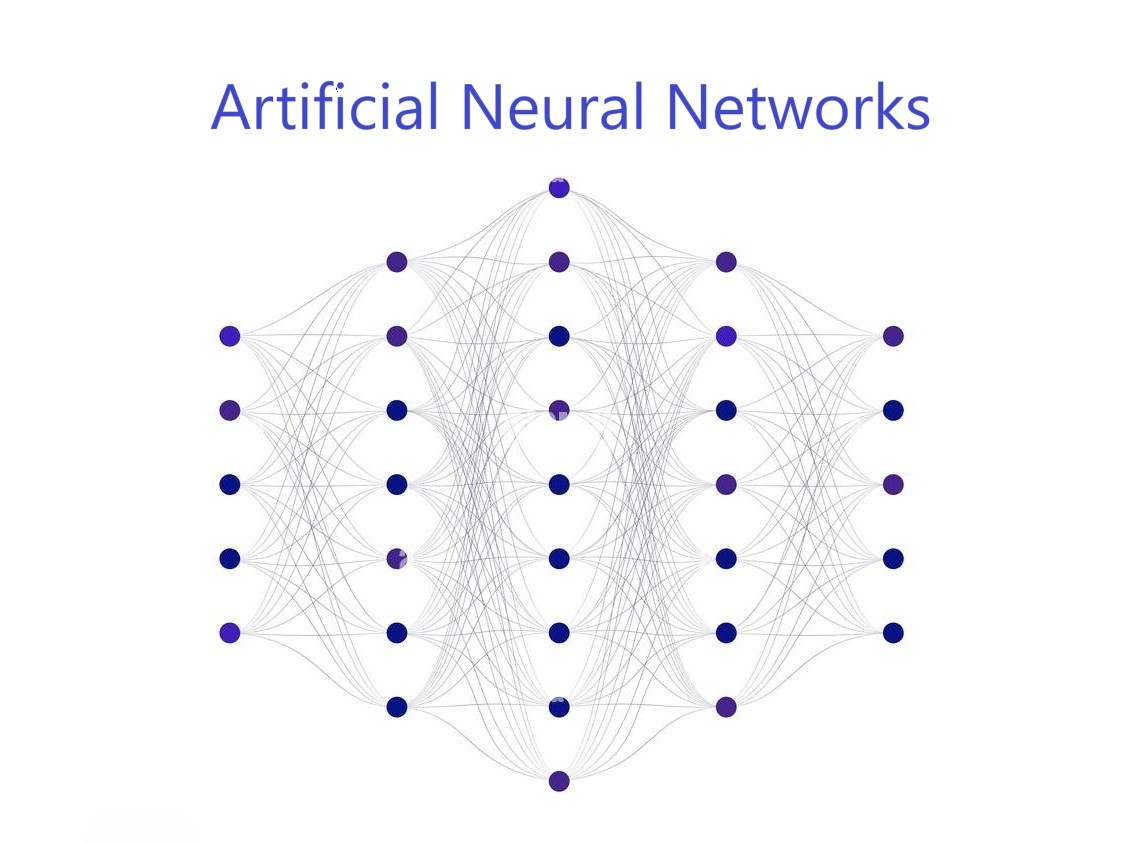





nonlinear activation function.
nonlinear activation function.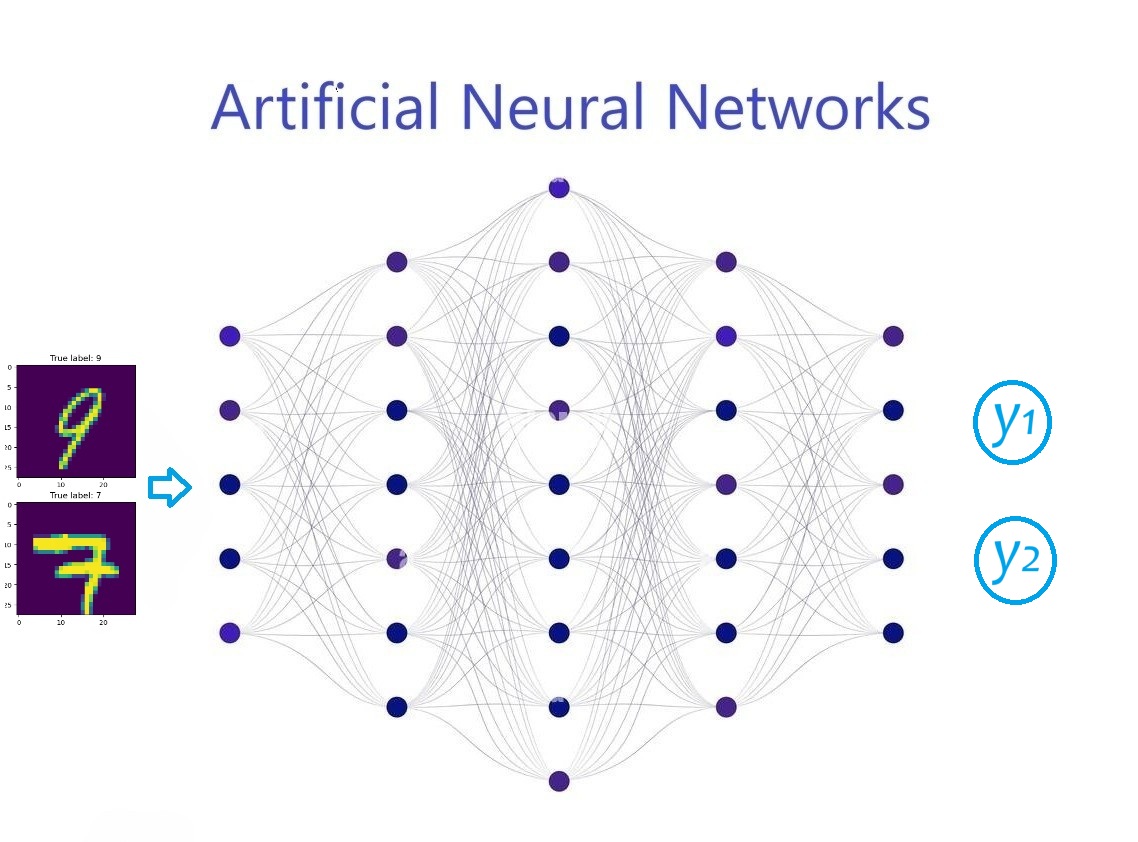

nonlinear activation function.

nonlinear activation function.Abalone dataset.| Sex | Length | Diameter | Height | Whole weight | Shucked weight | Viscera weight | Shell weight | Rings | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | M | 0.455 | 0.365 | 0.095 | 0.5140 | 0.2245 | 0.1010 | 0.150 | 15 |
| 1 | M | 0.350 | 0.265 | 0.090 | 0.2255 | 0.0995 | 0.0485 | 0.070 | 7 |
| 2 | F | 0.530 | 0.420 | 0.135 | 0.6770 | 0.2565 | 0.1415 | 0.210 | 9 |
| 3 | M | 0.440 | 0.365 | 0.125 | 0.5160 | 0.2155 | 0.1140 | 0.155 | 10 |
| 4 | I | 0.330 | 0.255 | 0.080 | 0.2050 | 0.0895 | 0.0395 | 0.055 | 7 |
Sex: OneHotEncoder.MinMaxScaler or StandardScaler.from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
data = data.loc[data.Height > 0,:] # drop missing values
data = pd.get_dummies(data, columns=['Sex'], drop_first=True) # One-hot encoding
X = data.drop('Rings', axis=1)
y = data['Rings']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # Train-test split
scaler = StandardScaler() # Scaling inputs
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
MLP using Keras.

Rings.\[\begin{align*} \text{Sigmoid}(z)&=1/(1+e^{-z})\text{ for }z\in\mathbb{R}\\ \text{Softmax}(z)&=(e^{z_1},\dots,e^{z_d})/\sum_{k=1}^de^{z_k},\text{ for }z\in\mathbb{R}^d\\ \color{red}{\text{ReLU}(z)}&\color{red}{=\max(0,z)\text{ for }z\in\mathbb{R}}\\ \text{Tanh}(z)&=\tanh(z)\text{ for }z\in\mathbb{R}\\ \text{Leaky ReLU}(z)&=\begin{cases}z,&\mbox{if} z>0\\ \alpha z,&\mbox{if }z\leq 0\end{cases}. \end{align*}\]
Gradient
GD Algorithm: Moving opposite to the gradient
for t=1,2,...,N: \[\color{blue}{\theta_{t}}:=\color{blue}{\theta_{t-1}}-\eta\nabla L(\color{blue}{\theta_{t-1}}).\]
if \(\|\nabla L(\color{blue}{\theta_{t^*}})\|<\delta\) at some step \(t^*\): return \(\color{blue}{\theta_{t^*}}\).else: return \(\color{blue}{\theta_{N}}\).GD Algorithm: Moving opposite to the gradient
for t=1,2,...,N: \[\color{blue}{\theta_{t}}:=\color{blue}{\theta_{t-1}}-\eta\nabla L(\color{blue}{\theta_{t-1}}).\]
if \(\|\nabla L(\color{blue}{\theta_{t^*}})\|<\delta\) at some step \(t^*\): return \(\color{blue}{\theta_{t^*}}\).else: return \(\color{blue}{\theta_{N}}\).SGD Algorithm: replace full data by small random subsets
approximate the full loss using small subsets of size \(b<<n\) called minibatches: \(\hat{L}_b(\color{blue}{\theta})=\frac{1}{b}\sum_{i=1}^b(y_i^B-\color{blue}{\hat{y}_i^B})^2.\)for t=1,2,...,N: \[\color{blue}{\theta_{t}}:=\color{blue}{\theta_{t-1}}-\eta\nabla \hat{L}_b(\color{blue}{\theta_{t-1}}).\]
if \(\|\nabla \hat{L}_b(\color{blue}{\theta_{t^*}})\|<\delta\) at some step \(t^*\): return \(\color{blue}{\theta_{t^*}}\).else: return \(\color{blue}{\theta_{N}}\).Model: "sequential_7"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓ ┃ Layer (type) ┃ Output Shape ┃ Param # ┃ ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩ │ dense_21 (Dense) │ (None, 32) │ 320 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_22 (Dense) │ (None, 32) │ 1,056 │ ├─────────────────────────────────┼────────────────────────┼───────────────┤ │ dense_23 (Dense) │ (None, 1) │ 33 │ └─────────────────────────────────┴────────────────────────┴───────────────┘
Total params: 1,409 (5.50 KB)
Trainable params: 1,409 (5.50 KB)
Non-trainable params: 0 (0.00 B)
batch_size: number of minibatch \(b\).epochs: number of times that the network passes through the entire training dataset.validation_split: a fraction of the training data for validation during model training. We can keep track of the model state during training by measuring the loss on this validation data, especially for preventing overfitting.# Training the network
history = model.fit(X_train, y_train, epochs=120, batch_size=32, validation_split=0.1, verbose=0)
# Extract loss values
train_loss = history.history['loss']
val_loss = history.history['val_loss']
# Plot the learning curves
epochs = list(range(1, len(train_loss) + 1))
fig1 = go.Figure(go.Scatter(x=epochs, y=train_loss, name="Training loss"))
fig1.add_trace(go.Scatter(x=epochs, y=val_loss, name="Training loss"))
fig1.update_layout(title="Training and Validation Loss",
width=510, height=200,
xaxis=dict(title="Epoch", type="log"),
yaxis=dict(title="Loss"))
fig1.show()Pros
Cons
