TP7 - Corresponding Analysis (CA)

Exploratory Data Analysis & Unsuperivsed Learning
Course: PHAUK Sokkey, PhD
TP: HAS Sothea, PhD

Objective: Qualitative columns are often ignored in predictive models or analysis. It is important to notice that qualitative variables are as important as the quantitative ones when it comes to building predictive models or analyzing their connection within the dataset. In this TP, we will focus on identifying the associations between two qualitative variables.

The Jupyter Notebook for this TP can be downloaded here: TP7_CA.ipynb.

1. Data loading and Preprocessing

Titanic dataset contains information on the passengers aboard the RMS Titanic, which sank in 1912. It includes details like age, gender, class, and survival status.

A. Import the Titanic dataset from kaggle using: Titanic dataset.

How many quantitative and qualitative variables are there in this dataset?
Convert each column into its correct data type.

import kagglehub

# Download latest version
path = kagglehub.dataset_download("surendhan/titanic-dataset")

# Import data
import pandas as pd
data = pd.read_csv(path + "/titanic.csv")
data.head()

	PassengerId	Survived	Pclass	Name	Sex	Age	SibSp	Parch	Ticket	Fare	Cabin	Embarked
0	892	0	3	Kelly, Mr. James	male	34.5	0	0	330911	7.8292	NaN	Q
1	893	1	3	Wilkes, Mrs. James (Ellen Needs)	female	47.0	1	0	363272	7.0000	NaN	S
2	894	0	2	Myles, Mr. Thomas Francis	male	62.0	0	0	240276	9.6875	NaN	Q
3	895	0	3	Wirz, Mr. Albert	male	27.0	0	0	315154	8.6625	NaN	S
4	896	1	3	Hirvonen, Mrs. Alexander (Helga E Lindqvist)	female	22.0	1	1	3101298	12.2875	NaN	S

data.dtypes

PassengerId      int64
Survived         int64
Pclass           int64
Name            object
Sex             object
Age            float64
SibSp            int64
Parch            int64
Ticket          object
Fare           float64
Cabin           object
Embarked        object
dtype: object

Survived and Pclass should be considered categorical. Let’s convert them.

data['Survived'] = data.loc[:,'Survived'].astype(object)
data['Pclass'] = data.loc[:,'Pclass'].astype(object)
data = data.drop(columns=['PassengerId'])

print(f'Quantitative columns: {data.select_dtypes(include="number").columns}')
print(f'Qualitative columns: {data.select_dtypes(include="object").columns}')

Quantitative columns: Index(['Age', 'SibSp', 'Parch', 'Fare'], dtype='object')
Qualitative columns: Index(['Survived', 'Pclass', 'Name', 'Sex', 'Ticket', 'Cabin', 'Embarked'], dtype='object')

B. Are there any missing values? If so,

Study the impact of missing value removal on the quantitative variables.
Study the impact of missing value removal on the qualitative variables.
Conclude the dynamic of the missing values and handle them.
Remove redundant observations if there is any.

data.isna().sum()

Survived      0
Pclass        0
Name          0
Sex           0
Age          86
SibSp         0
Parch         0
Ticket        0
Fare          1
Cabin       327
Embarked      0
dtype: int64

For column ‘Fare’, there is only one missing value. Therefore, we can simply drop it or impute it.
For column ‘Cabin’, around \(80\%\) of this column are missing values. It is not helpful to try to impute or remove the rows with missing values. Threfore, we simply drop this column.
The main column to be studied is ‘Age’. Therefore, we will study the impact of missing value removal from this column.

from sklearn.impute import SimpleImputer
data = data.drop(columns=['Cabin'])
sip = SimpleImputer(strategy='mean')
data['Fare'] = sip.fit_transform(data[['Fare']])

Impact on numerical columns

import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="whitegrid")

quant_cols = data.select_dtypes(include="number").columns
quant_cols

_, axs = plt.subplots(2, 3, figsize=(12, 5))

for i, va in enumerate(quant_cols[1:]):
  sns.kdeplot(data=data, x=va, ax=axs[0,i])
  axs[0,i].set_title(f'Distribution of {va} before removing NA')

  sns.kdeplot(data=data.dropna(), x=va, ax=axs[1,i])
  axs[1,i].set_title(f'Distribution of {va} after removing NA')
plt.tight_layout()
plt.show()

Impact on categorical columns

qual_cols = data.drop(columns=['Name', 'Ticket']).select_dtypes(include="object").columns
qual_cols
_, axs = plt.subplots(2, len(qual_cols), figsize=(18, 7))

for i, va in enumerate(qual_cols):
  sns.countplot(data=data, x=va, ax=axs[0,i])
  axs[0,i].set_title(f'Distribution of {va} before removing NA')
  axs[0,i].bar_label(axs[0,i].containers[0])

  sns.countplot(data=data.dropna(), x=va, ax=axs[1,i])
  axs[1,i].set_title(f'Distribution of {va} after removing NA')
  axs[1,i].bar_label(axs[1,i].containers[0])
plt.tight_layout()
plt.show()

2. \(\chi^2\)-test and CA

The chi-square test is a statistical method used to determine if there is a significant association between two categorical variables. It tests the following hypotheses: \[\begin{cases} H_0:\text{ There is no association between the two variables (they are independent).}\\ H_1:\text{ There is an association between the two variables (they are not independent).} \end{cases}\] Under null hypothesis \(H_0\), \(\chi^2\)-statistic defined by \(\chi^2=\sum_{i,j}\frac{(O_{ij}-E_{ij})^2}{E_{ij}}\sim\chi^2((r-1)(c-1))\) where

\(r,c\): the number of categories of the 1st and 2nd variable respectively.
\(O_{ij}\): the observed frequency of \(i\)-th and \(j\)-th category of the 1st and the 2nd variable.
\(E_{ij}\): the expected/theoretical frequency of \(i\)-th and \(j\)-th category of the 1st and the 2nd variable.

A. \(\chi^2\)-test for Pclass vs Embarked.

Visualize the relationship between the two variables.
Compute the \(\chi^2\) statistics of the pair Pclass and Embarked variable.
Deduce the p-value of \(\chi^2\)-test of the two variables.
Can we reject the null hypothesis \(H_0\) of the two variables being independent at \(95\%\) confidence level?
Recall the assumptions of \(\chi^2\)-test. Is the result about reliable?

import numpy as np
from scipy.stats import chi2_contingency

ax = sns.countplot(data=data[["Pclass", "Survived"]], x="Pclass", hue="Survived")
ax.set_title("Embarked chance within each class")
plt.show()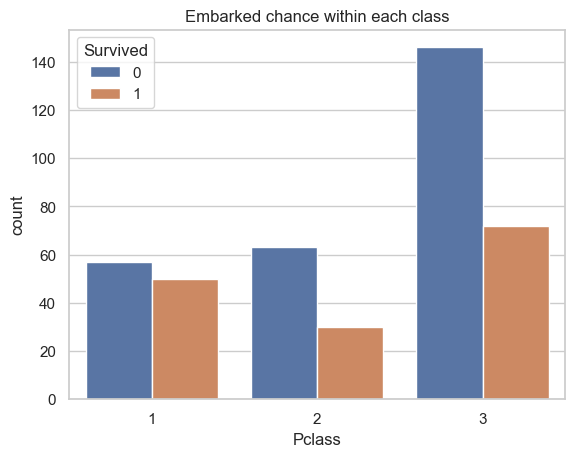

# Contingincy table
df = pd.crosstab(data['Pclass'], data['Survived'])
print(df)
# Row profile
C = df.sum(axis=0)
R = df.sum(axis=1)
E = R.values.reshape(-1,1) @ C.values.reshape(-1,1).transpose()/df.sum().sum()

chi_stat = np.sum((df-E) ** 2/E).sum()
print(f'* Chi-square statistic: {chi_stat}')

Survived    0   1
Pclass           
1          57  50
2          63  30
3         146  72
* Chi-square statistic: 6.693869422819262

c:\Users\hasso\AppData\Local\Programs\Python\Python312\Lib\site-packages\numpy\core\fromnumeric.py:86: FutureWarning:

The behavior of DataFrame.sum with axis=None is deprecated, in a future version this will reduce over both axes and return a scalar. To retain the old behavior, pass axis=0 (or do not pass axis)

from scipy.stats import chi2

# degree of freedom
dfr = 2
p_value = 1 - chi2.cdf(chi_stat, dfr)

print(f"The p-value associated with the chi-square statistic: {chi_stat} is {p_value}")

The p-value associated with the chi-square statistic: 6.693869422819262 is 0.03519206276590603

With p-value is close to zero, we can reject the null hypothesis of independence between the two variables with confidence level nearly 1.

B. Pclass vs Embarked:

Perform \(\chi^2\)-test on this pair of variables.
Perform CA on this pair of variables.
Create symmetric biplot of the resulting CA.
Interpret the result.

from scipy.stats import chi2_contingency
import prince

df = pd.crosstab(data['Pclass'], data['Embarked'])
chi2, p, dof, expected = chi2_contingency(df)

print(f'Chi-squrae staistic: {chi2} with p-value: {p}')

ca = prince.CA(n_components=2)
ca = ca.fit(df)

Chi-squrae staistic: 82.83186678873668 with p-value: 4.373384811850251e-17

row_coords = ca.row_coordinates(df)
col_coords = ca.column_coordinates(df)

# Plotting the results
plt.figure(figsize=(8, 6))
plt.scatter(row_coords[0], row_coords[1], c='red', s=100, label='Pclass')
plt.scatter(col_coords[0], col_coords[1], c='blue', s=150, label='Embarked')

class_label = {1: '1st', 2: '2nd', 3: '3rd'}

# Adding labels
for i, txt in enumerate(df.index.astype(object)):
    plt.annotate(txt, (row_coords[0].iloc[i], row_coords[1].iloc[i]+0.03), color='red')

for i, txt in enumerate(df.columns):
    plt.annotate(str(txt), (col_coords[0][i], col_coords[1][i]+ 0.03), color='blue')

plt.vlines(x=[0], ymax=0.7, ymin=-0.7, linestyles='--')
plt.hlines(y=[0], xmax=0.75, xmin=-0.75, linestyles='--')
plt.title('Correspondence Analysis: Pclass by Embarked')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.legend()
plt.grid()
plt.show()

C:\Users\hasso\AppData\Local\Temp\ipykernel_17636\1543237411.py:16: FutureWarning:

Series.__getitem__ treating keys as positions is deprecated. In a future version, integer keys will always be treated as labels (consistent with DataFrame behavior). To access a value by position, use `ser.iloc[pos]`

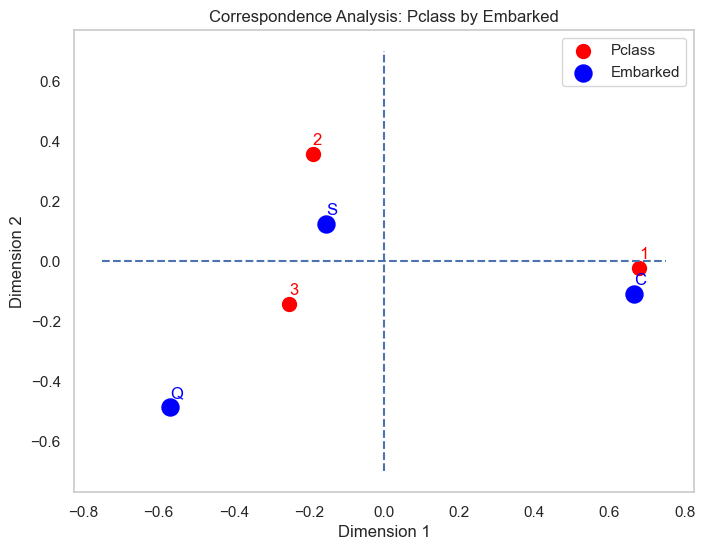
According to this map, it’s clear that

the 1st class passengers mostly embarked from Cherbourg
2nd class and some 3rd passengers embarked from Southampton
Queenstown is the rare category (deviated away from the origin than other variables) of Embarked and seem to be associated with the third class passengers than the rest.

3. Eye and Hair color

Study the connection between eye and hair colors from the Eye & Hair Color dataset available in kaggle as Hair Eye Color.

import kagglehub

# Download latest version
path = kagglehub.dataset_download("jasleensondhi/hair-eye-color")
data = pd.read_csv(path+'/HairEyeColor.csv')
data.head()

	Unnamed: 0	Hair	Eye	Sex	Freq
0	1	Black	Brown	Male	32
1	2	Brown	Brown	Male	53
2	3	Red	Brown	Male	10
3	4	Blond	Brown	Male	3
4	5	Black	Blue	Male	11

We sum along variable ‘Sex’ as we are interested in the relation between ‘Hair’ and ‘Eye’. We compute the join distribution of these two variables from the join frequency as follow:

df = data.pivot_table(index='Hair', columns='Eye', values='Freq', aggfunc='sum', fill_value=0)
df

Eye	Blue	Brown	Green	Hazel
Hair
Black	20	68	5	15
Blond	94	7	16	10
Brown	84	119	29	54
Red	17	26	14	14

We perform \(\chi^2\)-test on the two variables

chi2, p, dof, expected = chi2_contingency(df)
print(f'Chi-squrae staistic: {chi2} with p-value: {p}')

Chi-squrae staistic: 138.28984162600827 with p-value: 2.3252867870988044e-25

With such a low p-value, we can reject the null hypothesis the independency hypothesis between the two

import prince

ca = prince.CA(n_components=3).fit(df)
print(f'Variance explained by the first two dimensions:\n {ca.eigenvalues_summary}')

Variance explained by the first two dimensions:
           eigenvalue % of variance % of variance (cumulative)
component                                                    
0              0.209        89.37%                     89.37%
1              0.022         9.51%                     98.89%
2              0.003         1.11%                    100.00%

import plotly.io as pio
pio.renderers.default = 'notebook'

ca.plot(df, show_column_labels=True, show_row_markers=True, show_row_labels=True)

The first two dimensions can explain more than 98% of the total inertia of the data. Based on this biplot, one can see the association between eye and hair color as follow:

People who are blond tend to have blue eye color.
People with red hair color tend to have green eye color. Moreover, this appears to be rare eye color as it deviates away from the origin.
The graph also suggest that people with hazel eye color seen to have brown hair color and also red.
Lastly, black hair people are likely to have brown eye color.

4. Countries and languages

Reproduce results of the association between countries and primary language spoken within those countries conducted here. The contingency table of country of residence and primary language spoken is given below:

Country Language	English	French	Spanish	German	Italian	Total
Canada	688	280	10	11	11	1000
USA	730	31	190	8	41	1000
England	798	74	38	31	59	1000
Italy	17	13	11	15	944	1000
Switzerland	15	222	20	648	95	1000
Total	2248	620	269	713	1150	5000

You should work out this part as a real practical task by following this article.

# To do

1. Data loading and Preprocessing

2. \(\chi^2\)-test and CA

3. Eye and Hair color

4. Countries and languages

Further Readings