Model Evaluation

CSCI-866-001: Data Mining & Knowledge Discovery

Lecturer: Dr. Sothea HAS

🗺️ Content

Model Evaluation

• Review: Metrics
• Out-of-Sample Metrics
• \(K\)-fold Cross-Validation

Model Refinement

• Feature Engineering
• Overfitting
• Overcoming overfitting

1. Model Evaluation

Review: Metrics

Classification metrics

Confusion matrix

• \(\color{purple}{\text{Precision}}=\frac{\color{CornflowerBlue}{\text{TP}}}{\color{CornflowerBlue}{\text{TP}}+\color{purple}{\text{FP}}}:\) Controls \(\color{purple}{\text{FP}}\).
• \(\color{Tan}{\text{Recall}}=\frac{\color{CornflowerBlue}{\text{TP}}}{\color{CornflowerBlue}{\text{TP}}+\color{Tan}{\text{FN}}}:\) Controls \(\color{Tan}{\text{FN}}\).
• \(\color{ForestGreen}{\text{F1-score}}=\frac{2.\color{purple}{\text{Precision}}.\color{Tan}{\text{Recall}}}{\color{purple}{\text{Precision}}+\color{Tan}{\text{Recall}}}\).

• Example: Two models predict:

	0	1	2	3	4	5	6	7	8	9
Target	1	1	0	1	0	1	1	0	0	1
Pred1	1	0	0	1	0	1	0	1	0	1
Pred2	0	1	1	0	1	1	1	0	1	1

• Model 1:

• Accuracy: 0.7.
• Recall: 0.67.
• Precision: 0.8.
• F1-score: 0.73.

• Model 2:

• Accuracy: 0.5.
• Recall: 0.67.
• Precision: 0.57.
• F1-score: 0.62.

Classification metrics

Receiver Operating Characteristic Curve (ROC)

• For probabilistic models:
  • Logistic regression
  • Ensemble methods…

\(\bullet\) ROC \(=\{(\)FPR\(_{\delta}\),TPR\(_{\delta}):\delta\in[0,1]\}\).
\(\bullet\) Better model = Larger AUC.

• Example: a model with predictions:

	0	1	2	3	4	5	6	7	8	9
Target	1.00	1.00	0.00	1.00	0.0	1.0	1.0	0.00	0.00	1.00
Pred_prob	0.78	0.67	0.45	0.55	0.6	0.7	0.4	0.47	0.36	0.72

Classification metrics (Summary)

Confusion matrix

• Precision: controlls FP.
• Recall: controlls FN.
• F1-score: ballances the two.

ROC Curve & AUC

• ROC Curve: ballances TPR and FPR.
• Can be used to select \(\delta\in [0,1]\).
• Better model = Larger AUC.

Classification metrics

Losses vs Metrics

• Don’t confuse loss functions with metrics!

• Losses are used to train a model:
  • Log-loss/Cross-entropy: logistic regression.
  • Gini: train decision trees…

• Metrics are used to measure the performance of a built model.

🔑 Model evaluation is done based on suitable metrics.

Out-of-sample Metrics

Out-of-sample Metrics

• A good model must not only performs well on the training data (used to build it), but also on new unseen observations.

• We should judge a model based on how it generalizes to new unseen observations.

• In practice:

• Train data \(\approx80\%\) for building the model.
• Test data \(\approx20\%\) for testing the model’s performance.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2 # input, target, test size
)

Out-of-sample Metrics

Example: Simulated Data

	X1	X2	y
0	0.323036	-0.010089	0
1	0.410868	1.879064	1
2	0.261385	1.692064	1

• Data splitting: \(80\%-20\%\).
• Model: Logistic regression.

import seaborn as sns

# Model
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
colors = px.colors.qualitative.Set1[:2]
X_train, X_test, y_train, y_test = train_test_split(
    X, y.astype(int), test_size=0.2 # input, target, test size
)
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

lg1 = LogisticRegression()
lg1 = lg1.fit(X_train_scaled, y_train)

y_hat = lg1.predict(X_test_scaled)
pred_prob = lg1.predict_proba(X_test_scaled)[:,1]

metrics = {
    'Accuracy': accuracy_score,
    'Recall': recall_score,
    'Precision': precision_score,
    'F1-score': f1_score,
    'AUC': roc_auc_score}

perf_tab = pd.DataFrame(
    {key: metrics[key](y_test, y_hat) if key!="AUC" else metrics[key](y_test, pred_prob) for key in metrics.keys()},
    index=['Logit']
)
perf_tab

	Accuracy	Recall	Precision	F1-score	AUC
Logit	0.83	0.86	0.811321	0.834951	0.938

\(K\)-fold Cross-Validation

\(K\)-fold Cross-Validation

• What if we are unlucky?

\(K\)-fold Cross-Validation

• What if we are unlucky?

	Accuracy	Recall	Precision	F1-score	AUC
Logit	0.830000	0.860000	0.811321	0.834951	0.938000
Bad split	0.692308	0.670103	1.000000	0.802469	0.833579

• Here, the training data are less representative for the testing ones.

• Cross-validation is a technique to overcome this problem!

• \(K\)-fold CV with F1-score: \(\color{RoyalBlue}{\text{CV-F1}}=\frac{1}{K}\sum_{k=1}^K\color{green}{\text{F1-score}_k}.\)

• Ex: Computing CV-F1:

• It doesn’t depend on bad splits!
• It’s the average of different Test F1-score.
• It’s the Estimate F1-score of New Unseen Observations\(^{\text{📚}}\).

\(^{\text{📚}}\) Chapter 5, The Introduction to Statistical Learning.

:::

\(K\)-fold Cross-Validation

Summary

• Cross-validation is a model evaluation teachnique.
• It can be used with different metrics other than F1-score, such as Accuracy, Recall, Precision,…
• It can prevent overfitting.
• For Logistic Regression (without hyperparameter tuning), it can provide an estimate of average F1-score of unseen observations.
• For models with hyperparameters, it can be used to tune those values.

• Our toy example 10-fold CV-F1,

	Accuracy	Recall	Precision	F1-score	AUC
Logit	0.830000	0.860000	0.811321	0.834951	0.938000
Bad split	0.692308	0.670103	1.000000	0.802469	0.833579
Split 1	0.840000	0.818182	0.818182	0.818182	0.946834
Split 2	0.820000	0.727273	0.842105	0.780488	0.927760
Split 3	0.820000	0.760000	0.863636	0.808511	0.920800
Split 4	0.850000	0.760870	0.897436	0.823529	0.955717
Split 5	0.810000	0.784314	0.833333	0.808081	0.936775
Split 6	0.820000	0.813953	0.777778	0.795455	0.930641
Split 7	0.780000	0.765957	0.765957	0.765957	0.900040
Split 8	0.810000	0.825000	0.733333	0.776471	0.923750
Split 9	0.760000	0.767442	0.702128	0.733333	0.901673
CV-F1	0.800000	0.769000	0.823000	0.791000	0.918000

2. Model Refinement

Feature Engineering

Feature Engineering

Polynomial Features

• Sometimes, introducing the transformation of the original input features can result in a better model.
• Ex: Polynomial features: \(X_1,\dots,X_d\to X_i^kX_j^{p-k}, k=0,1,\dots,p\).

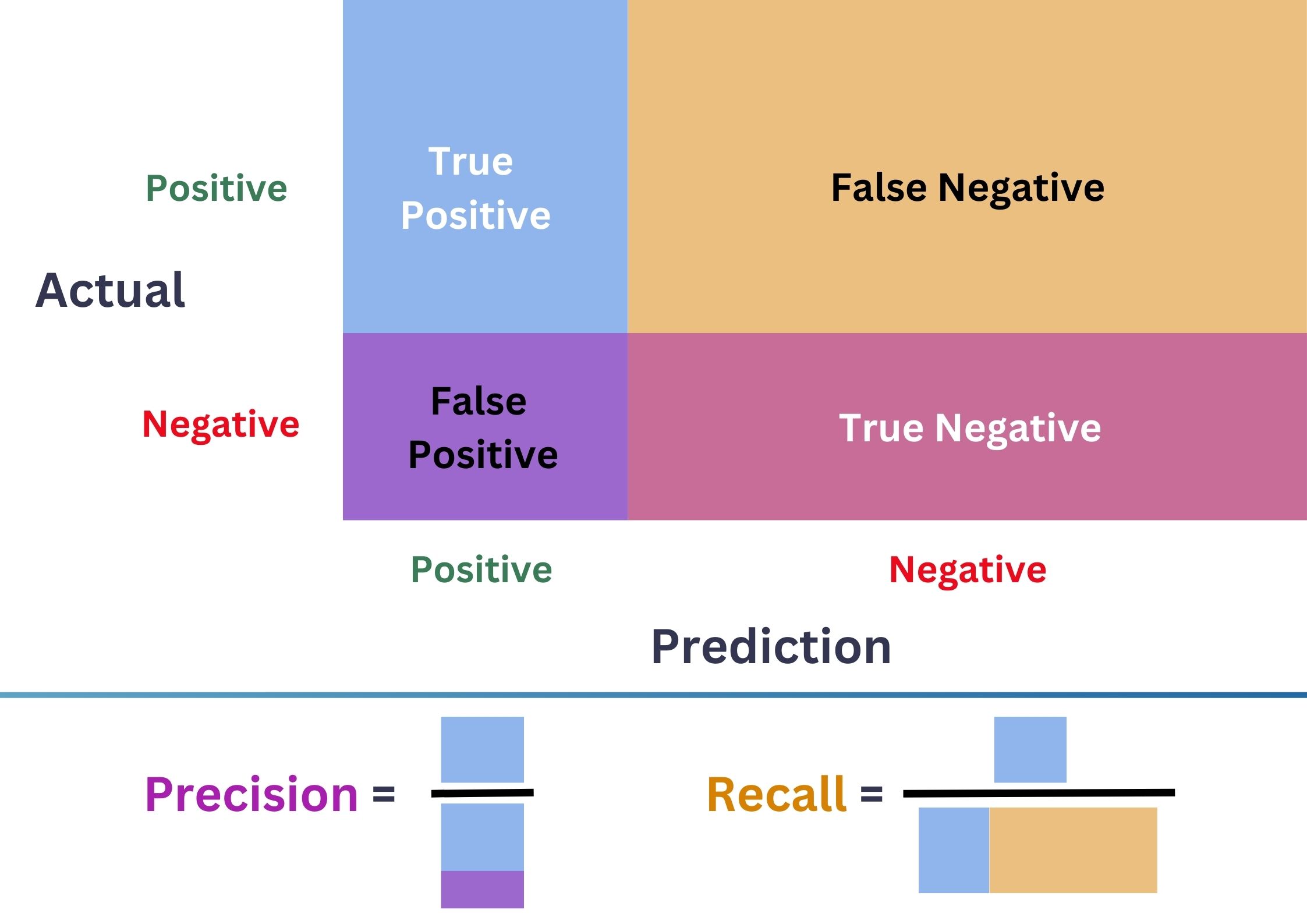
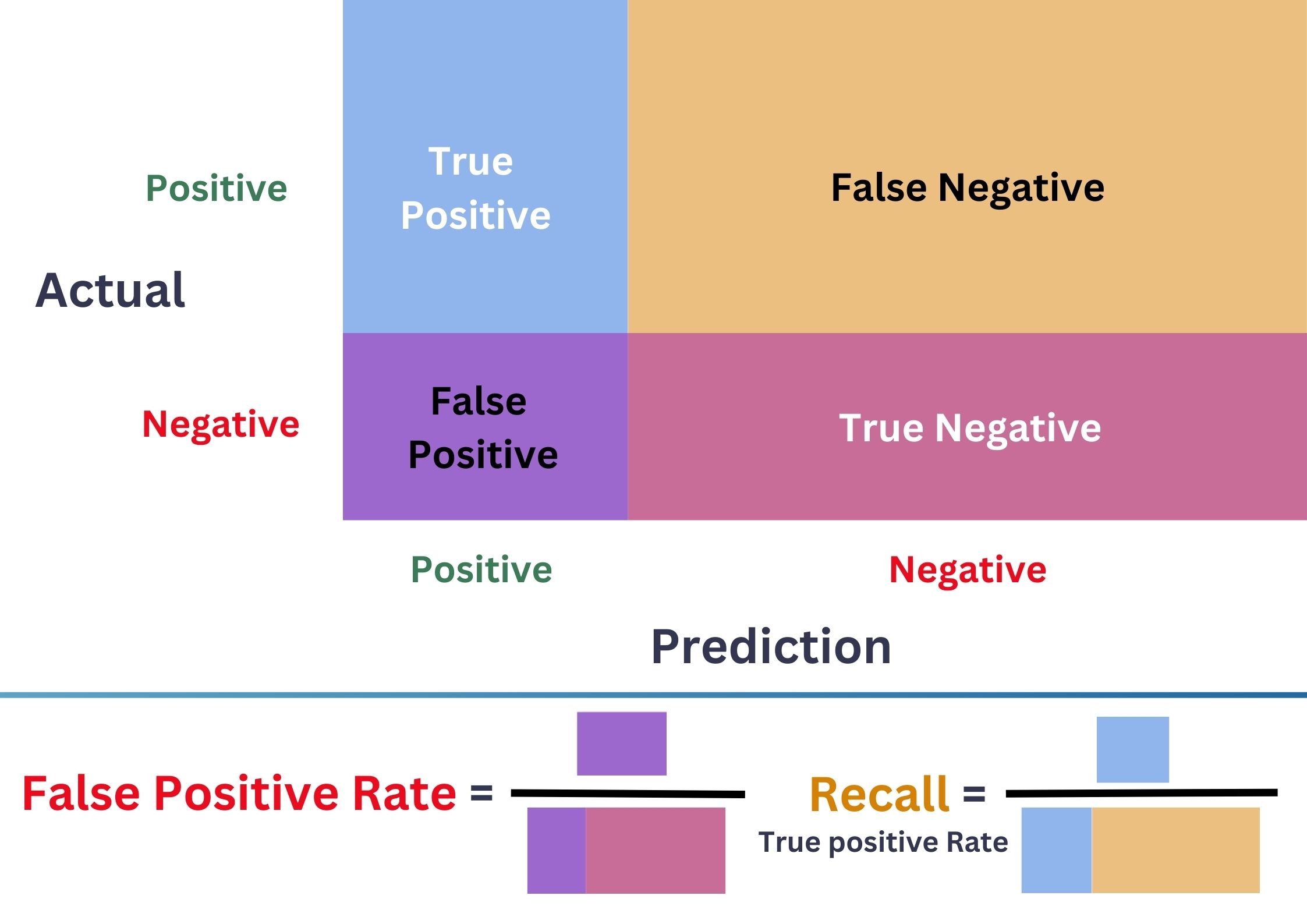
from sklearn.preprocessing import PolynomialFeatures

list_mod = []
degrees = [2,3,4,5,6,7,8,9,10,11,12,13,14,15]
for deg in degrees:
    poly = PolynomialFeatures(degree=deg, include_bias=True)
    X_poly_train = poly.fit_transform(X_train)
    X_poly_test = poly.transform(X_test)

    lg2 = LogisticRegression()
    lg2 = lg2.fit(X_poly_train, y_train)
    list_mod.append(lg2)
    y_hat = lg2.predict(X_poly_test)
    pred_prob = lg2.predict_proba(X_poly_test)[:,1]
    if deg == 2:
        perf_tab2 = pd.concat([perf_tab_cv.iloc[[0,-1],:], pd.DataFrame(
            {key: metrics[key](y_test, y_hat) if key!="AUC" else metrics[key](y_test, pred_prob) for key in metrics.keys()},
            index=['Poly2'])], axis=0
        )
    else:
        perf_tab2 = pd.concat([perf_tab2, pd.DataFrame(
            {key: metrics[key](y_test, y_hat) if key!="AUC" else metrics[key](y_test, pred_prob) for key in metrics.keys()},
            index=[f'Poly{deg}'])], axis=0
        )
perf_tab2

	Accuracy	Recall	Precision	F1-score	AUC
Logit	0.83	0.860	0.811321	0.834951	0.9380
CV-F1	0.80	0.769	0.823000	0.791000	0.9180
Poly2	0.84	0.820	0.854167	0.836735	0.9392
Poly3	0.89	0.860	0.914894	0.886598	0.9508
Poly4	0.91	0.880	0.936170	0.907216	0.9744
Poly5	0.93	0.880	0.977778	0.926316	0.9880
Poly6	0.93	0.880	0.977778	0.926316	0.9928
Poly7	0.93	0.880	0.977778	0.926316	0.9940
Poly8	0.93	0.880	0.977778	0.926316	0.9932
Poly9	0.92	0.860	0.977273	0.914894	0.9900
Poly10	0.90	0.820	0.976190	0.891304	0.9848
Poly11	0.90	0.820	0.976190	0.891304	0.9892
Poly12	0.90	0.820	0.976190	0.891304	0.9828
Poly13	0.90	0.820	0.976190	0.891304	0.9824
Poly14	0.89	0.840	0.933333	0.884211	0.9720
Poly15	0.89	0.860	0.914894	0.886598	0.9684

• Offer more flexible boundaries.
• May be more suitable in complex problems.
• Higher risk of overfitting!!!

Overfitting

Overfitting

Challenge in every model

• Overfitting happens when a model learns the training data too well, capturing noise and fluctuations rather than the underlying pattern.
• In this case, the model fits the training data almost perfectly, but fails to generalize to new, unseen data.
• Complex models (high-degree poly. features) often overfit the data.

Overcome Overfitting

Overcome Overfitting

Cross-Validation

• Strategies can be used to overcome overfitting:
  • Cross-validation methods
  • Regularization/penalty methods
  • Bootstrap/sampling techniques…
• Cross-validation methods can not only be used to overcome overfitting but also fine-tune suitable hyperparameters of ML models.
• Ex: fine-tune suitable degree of polynomial features:

from sklearn.model_selection import cross_val_score
scores= []
for deg in degrees:
    poly = PolynomialFeatures(degree=deg, include_bias=True)
    X_poly_train = poly.fit_transform(X_train)
    model = LogisticRegression()
    score = cross_val_score(
        model, X_poly_train, y_train, cv=5, 
        scoring='f1').mean()
    scores.append(score)

scores = np.array(scores)
fig = go.Figure(go.Scatter(
    x=degrees, y=scores,
    mode="markers+lines",
    name="F1-score",
    showlegend=True,
    marker=dict(color="red"),
    line=dict(color="red")))
max_score = scores.max()
degrees = np.array(degrees)
best_deg = degrees[scores == max_score][0]
fig.add_trace(
    go.Scatter(
        x=[best_deg]*2,
        y=[0.7, max_score],
        mode="markers+lines",
        name="Optimal degree",
        line=dict(color="green", dash="dash"),
        marker=dict(color="green"))
)
fig.update_layout(
    width=450, height=300,
    title="F1-score vs degree",
    xaxis=dict(title="Degree"),
    yaxis=dict(title="F1-score"))
fig.show()

	Accuracy	Recall	Precision	F1-score	AUC
Poly15	0.92	0.86	0.977273	0.914894	0.99

Model Evaluation Summary

• Model evaluation is about measuring the performance of a considered ML model using suitable metrics.
• Performance of an ML model should be judged based on new unseen data (ones omitted when training the model).
• Cross-validation can be used for:
  • Fine-tuning hyperparameters of the models: the degree of polynomial features, \(K\) for \(K\)NN, or number of trees in random forest…
  • Estimate the score for new observations…
• Best model \(\approx\) the one with the best cross-validation score.
• Similarly, best hyperparameter \(\approx\) ones provide the best cross-validation score.

🥳 It’s party time 🥂