🧊 Dimensional Reduction


CSCI-866-001: Data Mining & Knowledge Discovery



Lecturer: Dr. Sothea HAS

🗺️ Content

  • Motivation

  • Correlation matrix

  • Principal Component Analysis (PCA)

  • Dimensional Reduction & Reconstruction

  • Correlation Circle

  • t-distribution Stochastic Neighbor Embeding (t-SNE)

  • Autoencoder

Motivation

Motivation

California Housing Prices dataset

  • The data contains information from the 1990 California census.
  • Dimension: (20640, 10). It describes blocks across California.
longitude latitude housing_median_age total_rooms total_bedrooms population households median_income median_house_value ocean_proximity
0 -122.23 37.88 41 880 129.0 322 126 8.3252 452600 NEAR BAY
1 -122.22 37.86 21 7099 1106.0 2401 1138 8.3014 358500 NEAR BAY
2 -122.24 37.85 52 1467 190.0 496 177 7.2574 352100 NEAR BAY
3 -122.25 37.85 52 1274 235.0 558 219 5.6431 341300 NEAR BAY
4 -122.25 37.85 52 1627 280.0 565 259 3.8462 342200 NEAR BAY
  • There are columns indicating economy and size of the houses of each neighborhood.
  • How can we summarize and visualize individual-column relationship of the data?

Correlation Matrix

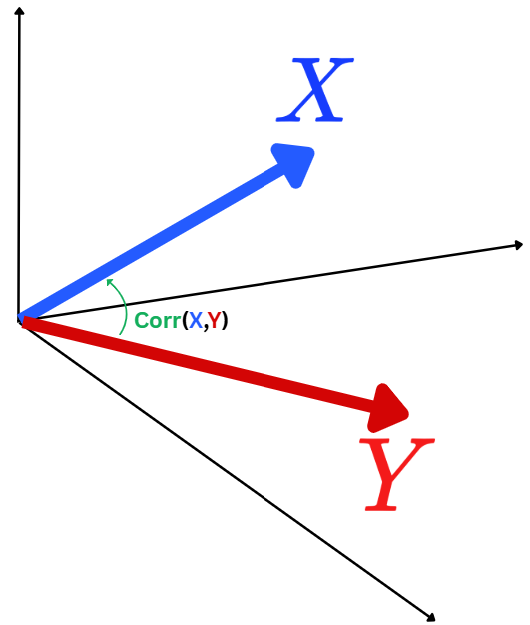
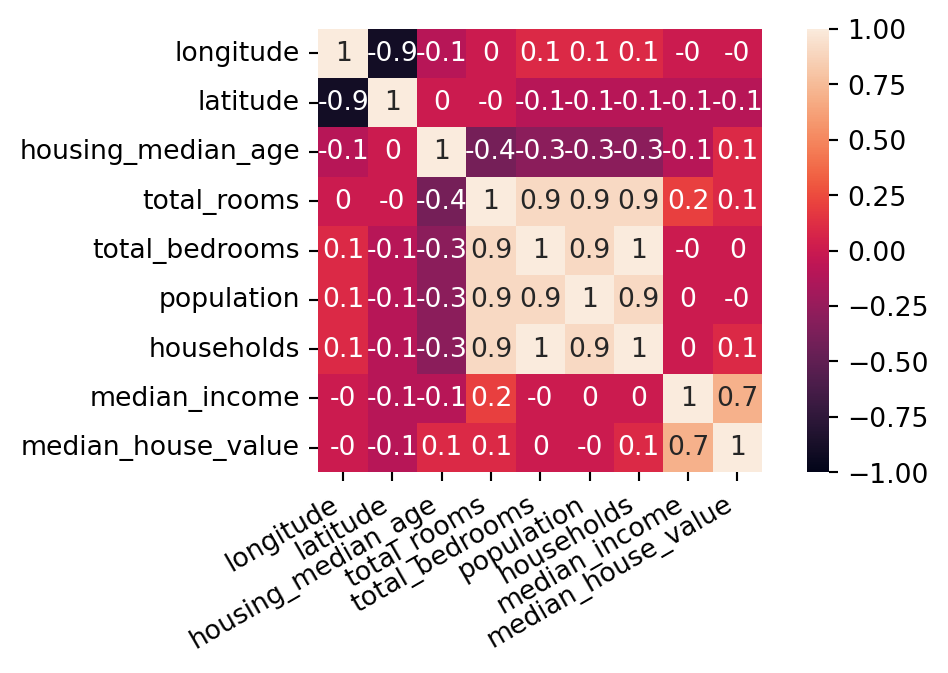
Correlation Matrix

Pearson’s Correlation Coefficients

  • Pearson’s corelation coefficient between two variables/columns \(\color{red}{X}=[\color{red}{x_1,...,x_n}]\) and \(\color{blue}{Y}=[\color{blue}{y_1,...,y_n}]\) measures their linear relationship and is defined by \[\text{Corr}(\color{red}{X},\color{blue}{Y})=\frac{\sum_{i=1}^n(\color{red}{x_i-\overline{x}_n})(\color{blue}{y_i-\overline{y}_n})}{\sqrt{\sum_{i=1}^n(\color{red}{x_i-\overline{x}})^2\sum_{i=1}^n(\color{blue}{y_i-\overline{y}})^2}}=\frac{\text{Cov}(\color{red}{X},\color{blue}{Y})}{\sigma_{\color{red}{X}}\sigma_{\color{blue}{Y}}}.\]
  • Properties:
    • \(-1\leq \text{Corr}(\color{red}{X},\color{blue}{Y})\leq 1\) for any pair \(\color{red}{X}\) and \(\color{blue}{Y}\).
    • \(\text{Corr}(\color{red}{X},\color{blue}{Y})\approx -1\) indicates strong negative linear relationship.
    • \(\text{Corr}(\color{red}{X},\color{blue}{Y})\approx 1\) indicates strong positive linear relationship.
    • \(\text{Corr}(\color{red}{X},\color{blue}{Y})\approx 0\) indicates weak or non-linear relationship.

Correlation Matrix

California Housing Prices dataset

  • Correlation matrix of the dataset:
Code 
import matplotlib.pyplot as plt
import seaborn as sns
f, ax = plt.subplots(figsize=(6, 3))
corr = data.select_dtypes(include="number").corr().round(1)
sns.heatmap(corr, annot=True,
    vmin=-1.0, vmax=1.0,
    square=True, ax=ax)
ax.set_yticklabels(ax.get_yticklabels(), ha='right')
ax.set_xticklabels(ax.get_xticklabels(), rotation=30, ha='right')
plt.show()

  • Variables are clustered according to location, economy and size.
  • High correlations among columns suggest that information can be compressed/reduced.
  • Geometrically, the pattern of data can be represented in simpler/smaller dimension.
  • PCA can detect important directions of data and reduce dimension of the data.
  • The important directions may carry meaningful interpretation for summaring the data.
  • Let’s explore this…

Principal directions & components

Principal directions & components

Principal directions (PDs) & Components (PCs)

  • Given data matrix: \(X\in\mathbb{R}^{n\times d}\),
X Y Z
0 -0.959 -0.808 -1.409
1 -2.439 0.870 -1.008
2 0.661 0.043 1.787
3 -3.891 -1.206 -4.043
4 0.618 1.229 0.470
5 1.310 0.082 0.454
6 0.822 -2.479 -1.142
7 4.057 1.629 6.200
8 1.932 1.685 4.132

Principal directions & components

Principal directions (PDs) & Components (PCs)

Principal directions \(\vec{u}_k\)

  • First principal direction \(\color{red}{\vec{u}_1}\in\mathbb{R}^d\) is the direction that the data spreads or varies the most.
  • Second principal direction \(\color{green}{\vec{u}_2}\in\mathbb{R}^d\) is the direction that perpendicular to \(\color{red}{\vec{u}_1}\) and captures second largest variation of the data.
  • For \(3\leq k\leq d\), the \(k\)-th principal direction \(\color{blue}{\vec{u}_k}\in\mathbb{R}^d\) is the direction that perpendicular to \(\{\color{red}{\vec{u}_1},\color{green}{\vec{u}_2},\dots,\color{purple}{\vec{u}_{k-1}}\}\) and captures the \(k\)-th largest variation of the data.
  • Let \(U\) be a \(d\times d\) matrix with all PD columns, i.e., \[U=[\color{red}{\vec{u}_1}|\color{green}{\vec{u}_2}|\dots |\color{blue}{\vec{u}_d}],\] then \(\tilde{X}=XU\) is the rotated data with independent columns, and the 1st, 2nd, 3rd… columns has the largest, 2nd largest, 3rd largest… variance, respectively. They’re called Principal Components (PCs).

Principal directions & components

How to find PDs & PCs

Solution to Principal Directions \(\vec{u}_k\)

  • Let \(X\in\mathbb{R}^{n\times d}\) the data matrix.
  • PDs \(\color{red}{\vec{u}_1},\dots,\color{blue}{\vec{u}_d}\) are the 1st, …, \(d\)-th eigenvectors of matrix \(A=X^TX\) with eigenvalues \(\color{red}{\lambda_1}>\dots>\color{blue}{\lambda_d}\geq 0\) respectively.
  • Principal components are the columns of

\[\begin{align*} \underbrace{\tilde{X}}_{n\times d}&=\underbrace{X}_{n\times d}\underbrace{\color{blue}{U}}_{n\times d}\\ &=\begin{bmatrix} \text{x}_{11} & \dots & \text{x}_{1d}\\ \text{x}_{21} & \dots & \text{x}_{2d}\\ \text{x}_{31} & \dots & \text{x}_{3d}\\ \vdots & \ddots & \vdots\\ \text{x}_{n1} & \dots & \text{x}_{nd}\end{bmatrix} \begin{bmatrix} \text{u}_{11} & \dots & \text{u}_{1d}\\ \text{u}_{21} & \dots & \text{u}_{2d}\\ \vdots & \ddots & \vdots\\ \text{u}_{d1} & \dots & \text{u}_{dd}\end{bmatrix} \end{align*}\]

  • The \(j\)-th PC is the combination of original columns of \(X_i\), i.e., \(\text{PC}_j=\sum_{i=1}^du_{ij}X_i.\)

Principal directions & components

Implementation of PCA

Unnormalized PCA

  • Given data: \(X\in\mathbb{R}^{n\times d}\)
  • Centering \(X_c=\underbrace{X}_{n\times d} -\underbrace{\mathbb{1}_n}_{n\times n}\underbrace{X}_{n\times d}/n.\)
  • Perform Eigenvalue Decomposition on covariance matrix \(V=X_c^TX_c/(n-1)\): \[V=\color{blue}{U}\Sigma \color{blue}{U}^T,\]
    • \(\color{blue}{U}\): matrix of eigenvectors
    • \(\Sigma=\text{diag}(\lambda_1,\dots,\lambda_d)\): diagonal matrix of eigenvalues \(\lambda_1\geq \dots\geq \lambda_d\geq 0\).

Normalized PCA

  • Given data: \(X\in\mathbb{R}^{n\times d}\)
  • Standardizing: compute std matrix \(D=\text{diag}(\widehat{\sigma}_1,\dots,\widehat{\sigma}_d)\) and standardized data \(Z=(\underbrace{X}_{n\times d} -\underbrace{\mathbb{1}_n}_{n\times n}\underbrace{X}_{n\times d}/n)D^{-1}.\)
  • Perform Eigenvalue Decomposition on correlation matrix \(C=Z^TZ/(n-1)\): \[C=\color{blue}{U}\Sigma \color{blue}{U}^T.\]
  • Rotated data: \(\color{blue}{\tilde{X}}=X\color{blue}{U}.\) [👉 Demo]

Dimensional Reduction & Reconstruction

Reduction/Reconstruction

Dimensional Reduction

  • Reduction to \(k\) dimensions (\(k<d\)) is done by \(\color{blue}{\tilde{X}_k=\tilde{X}[:,:k]}.\)
  • Quality of representation on each direction: \(\left[\frac{\lambda_1}{\sum_{j=1}^d\lambda_j},\dots,\frac{\lambda_k}{\sum_{j=1}^d\lambda_j}\right].\)
  • Variation explained by \(k\) dimensions: \(\frac{\sum_{j=1}^k\lambda_j}{\sum_{j=1}^d\lambda_j}\times 100.\)
  • For visualization, one can choose \(k=2\) or \(3\). [👉 Demo]
* Total variation of X: 15.25
X Y Z
0 -0.959 -0.808 -1.409
1 -2.439 0.870 -1.008
2 0.661 0.043 1.787
3 -3.891 -1.206 -4.043
4 0.618 1.229 0.470 
* Total variation of projection: 15.2
PC1 PC2 PC3
0 -2.424 -0.173 -0.197
1 -2.287 2.086 -0.406
2 1.239 -0.292 -0.558
3 -6.119 1.163 -0.709
4 0.509 0.555 0.818

Reduction/Reconstruction

Dimensional Reduction

  • Reduction to \(k\) dimensions (\(k<d\)) is done by \(\color{blue}{\tilde{X}_k=\tilde{X}[:,:k]}.\)
  • Quality of representation on each direction: \(\left[\frac{\lambda_1}{\sum_{j=1}^d\lambda_j},\dots,\frac{\lambda_k}{\sum_{j=1}^d\lambda_j}\right].\)
  • Variation explained by \(k\) dimensions: \(\frac{\sum_{j=1}^k\lambda_j}{\sum_{j=1}^d\lambda_j}\times 100.\)
  • For visualization, one can choose \(k=2\) or \(3\). [👉 Demo]
  • Application on California Housing Price dataset:
  • Percentage of variance explained by two PCs: 79.86%.

Reduction/Reconstruction

Dimensional Reduction

  • Reduction to \(k\) dimensions (\(k<d\)) is done by \(\color{blue}{\tilde{X}_k=\tilde{X}[:,:k]}.\)
  • Quality of representation on each direction: \(\left[\frac{\lambda_1}{\sum_{j=1}^d\lambda_j},\dots,\frac{\lambda_k}{\sum_{j=1}^d\lambda_j}\right].\)
  • Variation explained by \(k\) dimensions: \(\frac{\sum_{j=1}^k\lambda_j}{\sum_{j=1}^d\lambda_j}\times 100.\)
  • For visualization, one can choose \(k=2\) or \(3\). [👉 Demo]

Reconstruction

  • The reconsution is defined by: \[\color{red}{X_k^{\text{rec}}}=\tilde{X}_k\color{blue}{U[:,:k]^T}.\]

  • Best low-rank approximation shows that this reconstruction \(\color{red}{X_k^{\text{rec}}}\) is the best \(k\)-rank approximation of \(X\) with respect to Frobenius norm, i.e., \[\color{red}{X_k^{\text{rec}}}=\arg\min_{M_k:r(M_k)\leq k}\|X-M_k\|_F,\] where \(\|.\|_F\) is the Frobenius norm.

Reduction/Reconstruction

Summary

  • PCA captures and arranges directions with largest, 2nd largest,… variation into the 1st, 2nd, … column using Spectral Theorem (Eigenvalue decomposition).
  • These directions are contained in the eigenvector matrix of Covariance (unnormalized) or Correlation matrix (normalized) of the data.
  • The variation along each direction is given by the corresponding eigenvalues: \(\lambda_1>\dots>\lambda_d\).
  • Our goal is to explore dimensional reduction and reconstruction power of PCA, however, it can be used in Data Analysis, EDA, Data Summary…
  • Remark: Many highly correlated columns indicates effective dimensional reduction (the first two PCs can capture significant variation).

Correlation Circle

Correlation Circles

  • Besides dimensional reduction, PCA can be used to analyze the data.
  • How would you explain this scatterplot?
  • One should understand the connection between PCs and the original columns.
  • This is done using Correlation Circle.
  • One can compute correlations between original data with PCs:
Code 
d = len(quan_cols)
combined_data = pd.concat([pd.DataFrame(Z[:,:2], columns=['PC'+str(i+1) for i in range(2)]), pd.DataFrame(X[:,2:], columns = quan_cols[2:])], axis=1)
Corr_matrix = combined_data.corr()[['PC'+str(i+1) for i in range(2)]].iloc[2:,:]
Corr_matrix
PC1 PC2
housing_median_age -0.426668 0.048696
total_rooms 0.963481 0.087248
total_bedrooms 0.971857 -0.077096
population 0.930272 -0.113646
households 0.975068 -0.059403
median_income 0.107198 0.912892
median_house_value 0.084727 0.913812
Code 
fig_cir = go.Figure()
circle = go.Scatter(
    x=np.cos(np.linspace(0, 2 * np.pi, 100)),
    y=np.sin(np.linspace(0, 2 * np.pi, 100)),
    mode='lines',
    name='Unit Circle',
    line=dict(color='black', dash='dash')
)
fig_cir.add_trace(circle)
fig_cir.add_trace(go.Scatter(
    x=[-1,1],
    y = [0,0],
    mode="lines", line=dict(color='gray', dash='dash')
))
fig_cir.add_trace(go.Scatter(
    x=[0,0],
    y = [-1,1],
    mode="lines", line=dict(color='gray', dash='dash')
))

loc = ['top right', 'top left', 'bottom right', 'bottom left', 'top right', 'top left', 'bottom right']

# Add loading vectors
for i, feature in enumerate(quan_cols[2:]):
    fig_cir.add_trace(go.Scatter(
        x=[0, Corr_matrix.iloc[i, 0]],
        y=[0, Corr_matrix.iloc[i, 1]],
        mode='lines+text',
        text=[None, feature],
        textposition=[loc[i]],
        name=feature,
        showlegend=True
    ))

# Set the layout
fig_cir.update_layout(
    title='Correlation Circle',
    xaxis=dict(title='PC1 ('+str(np.round(pca.explained_variance_ratio_[0]*100,2)) + '%)', range=[-1.2, 1.2]),
    yaxis=dict(title='PC2 ('+str(np.round(pca.explained_variance_ratio_[1]*100,2)) + '%)', range=[-1.2, 1.2]),
    showlegend=False,
    width=470,
    height=470
)
fig_cir.show()
Code 
fig_cor = fig_bi_house
fig_cor.add_trace(go.Scatter(
    x=[-1,1],
    y = [0,0],
    mode="lines", line=dict(color='gray', dash='dash')
))
fig_cor.add_trace(go.Scatter(
    x=[0,0],
    y = [-1,1],
    mode="lines", line=dict(color='gray', dash='dash')
))
for i, var in enumerate(quan_cols[2:]):
    fig_cor.add_shape(
        type='line',
        x0=0, y0=0,
        x1=Corr_matrix.iloc[i, 0]*2, y1=Corr_matrix.iloc[i, 1]*2
    )
    fig_cor.add_annotation(
        x=Corr_matrix.iloc[i, 0]+np.random.normal(0,0.25), y=Corr_matrix.iloc[i, 1]+np.random.normal(0,0.25),
        ax=0, ay=0,
        xanchor="center",
        yanchor="bottom",
        text=var
    )
fig_cor.update_layout(width=470, height=470)
fig_cor.show()

Correlation Circles

Interpretation

  • PC1 is strong related to total_rooms, households, population and housing_median_age.
  • PC2 is strong reated to median_income and median_house_value.
  • The length of each variable represents how well represented it is in the plane of PC1 and PC2 (1st factorial plane).
  • Highly correlated original variables are mostly aligned.
  • Those that are nearly perpendicular, tend to be decorrelated.
  • For this example:
    • PC1 seems to represent size and condition of houses within each block.
    • PC2 seems to represent economic condition of houses within each neighborhood.
  • This can be used to summarize the scatterplot of individuals.

Principal Component Analysis (PCA)

Summary

  • PCA captures and arranges directions with largest, 2nd largest,… variation into the 1st, 2nd, … column using Spectral Theorem (Eigenvalue decomposition).
  • These directions are contained in the eigenvector matrix of Covariance (unnormalized) or Correlation matrix (normalized) of the data.
  • The variation along each direction is given by the corresponding eigenvalues: \(\lambda_1>\dots>\lambda_d\).
  • Our goal is to explore dimensional reduction and reconstruction power of PCA, however, it can be used in Data Analysis, EDA, Data Summary…
  • Remark: Many highly correlated columns indicates effective dimensional reduction (the first two PCs can capture significant variation).

\(t\)-distribution Stochastic Neighbor Embedding (\(t\)-SNE)

Setting

  • Suppose \(X\in\mathbb{R}^{n\times d}\) with large \(d\).

Objective

\(t\)-SNE aims at finding lower dimensional (LD) representation of \(X\) (2 or 3) so that the distribution among LD data is similar to the original data.

Code 
from sklearn.manifold import TSNE

# Prepare the t-SNE model
tsne = TSNE(n_components=2, random_state=42)

# Fit and transform the data
X_tsne = tsne.fit_transform(X[:1000,:])  # Use a subset for faster computation
df_tsne = pd.DataFrame(X_tsne, columns=['Component 1', 'Component 2'])
df_tsne['label'] = y_train[:1000]
fig_tsne = px.scatter(df_tsne, x="Component 1", y="Component 2", color="label")
fig_tsne.update_layout(height=420, width=500, title="t-SNE visualization on MNIST")
fig_tsne.show()

\(t\)-distribution Stochastic Neighbor Embedding (\(t\)-SNE)

Original and embedding distribution in \(t\)-SNE

  • Gaussian similarity probability between original points \(\text{x}_i,\text{x}_j\in\mathbb{R}^d\): \[p_{i,j}=\frac{e^{-\|\text{x}_i-\text{x}_j\|^2/(2\sigma^2)}}{\sum_{k\neq \ell:k,\ell=1}^n e^{-\|\text{x}_k-\text{x}_{\ell}\|^2/(2\sigma^2)}}.\]

  • \(t\)-distribution probability between embedded data points \(\text{z}_i,\text{z}_j\in\mathbb{R}^{d'} (d'<d)\): \[q_{i,j}=\frac{(1+\|\text{z}_i-\text{z}_j\|^2)^{-1}}{\sum_{k\neq \ell:k,\ell=1}^n (1+\|\text{z}_k-\text{z}_{\ell}\|^2)^{-1}}.\]

\(t\)-SNE

Optimization for LD data \(z_i\)

  • In the first proposed method (SNE in Hinton and Roweis (2002)), \(q_{i,j}\) was also Gaussian similarity. This often leads to Crowding Problem.
  • Q1: How do we find LD data \(z_i\)?
  • We can measure the proximity between vector (or matrix) of similarity probabilities on HD data \(P=(p_{i,j})\) and on LD data \(Q=(q_{i,j})\) using Kullback-Leibler divergence: \[D_{KL}(P||Q)=\sum_{i,j}p_{i,j}\log\left(\frac{p_{i,j}}{q_{i,j}}\right).\]
  • Gradient of KL w.r.t \(z_i\):

\[\frac{\partial KL}{\partial z_i}=4\sum_{j}(p_{i,j}-q_{i,j})(z_i-z_j)(1+\|z_i-z_j\|^2)^{-1}.\]

Gradient Descent With Momentum

  • Data: \(X=\{\text{x}_1,\dots,\text{x}_n\}\).
  • Perplexity: Perp (effective local neighbors between 5 and 50).
  • Parameters: max_iter, learning rate: \(\eta\), momentum \(\alpha(t)\).
  • Result: LD data \(Z=\{z_1,\dots,z_n\}\).
  • Begin:
    • Compute \(p_{i,j}\)
    • Initialize: \(Z^{(0)}=\{z_1^{(0)},\dots,z_n^{(0)}\}\)
    • for t=1 to max_iter do:
      • Compute \(q_{i,j}\) and gradient: \(\frac{\partial KL}{\partial z_i}\)
      • Update: \(Z^{(t)}=Z^{(t-1)}+\eta\frac{\partial KL}{\partial z_i}+\alpha(t)(Z^{(t-1)}-Z^{(t-2)})\).
  • End. [👉 Demo]

\(t\)-SNE

Summary

  • \(t\)-SNE is a dimentional reduction technique aiming at searching for neighbors of points in a lower-dimensional space (2 or 3) especially for visualization.
  • High-dimensional data \(X\) is converted to pairwise similarity probability \(P=(p_{i,j})\) according to how close they are.
  • The pairwise similarity probability \(Q=(q_{i,j})\) of low-dimensional data points is defined based on \(t\)-distribution of degree 1 or Cauchy distribution.
  • The proximity between \(P\) and \(Q\) is measured using KL divergence.
  • The LD data \(z_i\) are estimated by minimizing KL divergence using Gradient Descent with Momontum.

AutoEncoders

Introduction

  • Autoencoders are a type of DNN used for learning efficient codings of input data.
  • It’s an unsupervised learning method that works by compressing data into a lower-dimensional representation (encoding) and then reconstructing it back to its original form (decoding).

AutoEncoders

Main components / Loss

  • Data: \(X\in\mathbb{R}^{n\times d}\).
  • Encoder: \(E:\mathbb{R}^d\to\mathbb{R}^{d'}\) encodes original data into lower-dimensional representation called Latent Representation.
  • Decoder: \(D:\mathbb{R}^{d'}\to\mathbb{R}^{d}\) reconstructs back the original data from their Latent Representation.

Loss

  • Training optimal \(\color{blue}{E^*}\) and \(\color{blue}{D^*}\) networks can be simply formulated as: \[(\color{blue}{E^*},\color{blue}{D^*})=\arg\min_{E,D} \frac{1}{n}\sum_{i=1}^n\ell(\text{x}_i,D[E(\text{x}_i)]).\]

  • This is equivalent to training two neural networks at once.

  • AE is in fact a generalization of PCA, while PCA finds the optimal linear subs-space (hyperplane) for the projected data, AE is able to learn non-linear manifold embedding [see Elad Plaut (2018)].

AutoEncoders

Other types

  • Sparse Autoencoders: \(\color{blue}{E^*}\) and \(\color{blue}{D^*}\) networks are trained with penalization.
    • \(L_1\) regularization for regression: \[(\color{blue}{E^*},\color{blue}{D^*})=\arg\min_{E,D} \frac{1}{n}\sum_{i=1}^n\ell(\text{x}_i,D[E(\text{x}_i)])+\lambda\sum|\color{blue}{W}_{E,D}|.\]
    • KL divergence for classification: \[(\color{blue}{E^*},\color{blue}{D^*})=\arg\min_{E,D} \frac{1}{n}\sum_{i=1}^n\ell(\text{x}_i,D[E(\text{x}_i)])+\lambda\sum_{j}\color{blue}{\text{KL}}(p\|\hat{p}_j).\]

AutoEncoders

Other types

  • Denoising Autoencoders: \(\color{blue}{E^*}\) and \(\color{blue}{D^*}\) networks are trained just like before, and the noisy input \(\tilde{\text{x}}_i\) is obtained by, for example, \(\tilde{\text{x}}_i\sim {\cal N}(\text{x}_i,\sigma^2I_d).\)

🥳 It’s party time 🥂