Classification: Naive Bayes Classifier & Logistic Regression


CSCI-866-001: Data Mining & Knowledge Discovery



Lecturer: Dr. Sothea HAS

📋 Outline

  • Naive Bayes Classifier (NBC)
    • Motivation and Introduction to Classification
    • NBC Model Setting and Main Assumption
    • Application
    • Handling Imbalanced Data
  • Logistic Regression
    • Model setting and Intuition
    • Conditional Likelihood and Loss function
    • Optimization: GD and SGD
    • Application

1. Naive Bayes Classifier (NBC)

Motivation

Motivation

  • We humans can effortlessly recognize cats and dogs:

  • No sweat even with these kind of patterns:

  • How can we make a computer program learns to do this?
  • Other than cats & dogs, it’s much more useful to identify
    • Email spams
    • Frauds in banking systems
    • Diseases in health care system…

Motivation

Classification in Machine Learning

  • Machine Learning (ML): a branch of AI focused on enabling computers/machines to imitate the way that humans learn.

  • Three main branches:
    • Supervised Learning: for predicting some target (categorical or numerical).
    • Unsupervised Learning: for grouping, understanding and reducing the dimension of the data (not for predicting).
    • Reinforcement Learning: a model works on some tasks and learn to improve itself based on how it’s performed so far.

Motivation

Classification in Machine Learning

  • Machine Learning (ML): a branch of AI focused on enabling computers/machines to imitate the way that humans learn.

  • Supervised Classification: Predicting qualitative/categorical target.
  • Three main branches:
    • Supervised Learning: for predicting some target (categorical or numerical).
    • Unsupervised Learning: for grouping, understanding and reducing the dimension of the data (not for predicting).
    • Reinforcement Learning: a model works on some tasks and learn to improve itself based on how it’s performed so far.

NBC Model Setting and Main Assumption

Naive Bayes Classifiers (NBC)

Consider Email spam dataset ✉️

make address all num3d our over remove internet order mail ... charSemicolon charRoundbracket charSquarebracket charExclamation charDollar charHash capitalAve capitalLong capitalTotal type
0 0.00 0.64 0.64 0.0 0.32 0.00 0.00 0.00 0.00 0.00 ... 0.00 0.000 0.0 0.778 0.000 0.000 3.756 61 278 spam
1 0.21 0.28 0.50 0.0 0.14 0.28 0.21 0.07 0.00 0.94 ... 0.00 0.132 0.0 0.372 0.180 0.048 5.114 101 1028 spam
2 0.06 0.00 0.71 0.0 1.23 0.19 0.19 0.12 0.64 0.25 ... 0.01 0.143 0.0 0.276 0.184 0.010 9.821 485 2259 spam

3 rows × 58 columns

  • Input \(\text{x}_i=(x_{i1},x_{i2},\dots, x_{id})\): Bag of words of email \(i\).
  • Target \(y_i\in\{1,0\}\) with \(1=\) spam and \(0=\) nonspam.
  • Objective: Classify if an email is a spam or not based on its input.
  • Data shape: (4601, 58).
  • Total missing values: 0.
  • Total duplicated rows: 391.
  • After removing duplicates:
Code 
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="whitegrid")
_, ax = plt.subplots(1,1,figsize=(3,2.15))
spam.drop_duplicates(inplace=True)
sns.countplot(data=spam, x="type", hue="type", stat="percent")
ax.set_title("Barplot of Email  Type")
ax.bar_label(ax.containers[0], fmt="%.2f")
ax.bar_label(ax.containers[1], fmt="%.2f")
plt.show()

Naive Bayes Classifiers (NBC)

Model Motivation

  • Given an email (input) \(\text{x}_i=(0, 0.64,\dots,278)\in\mathbb{R}^{57}\), how would you guess its type \(y_i\)?
  • 🔑 The most important quantity in (binary) classification: \[\color{blue}{\mathbb{P}(Y_i=1|X=\text{x}_i)}.\] Interpretation: Given input \(\text{x}_i\), how likely that it belongs to class 1 (spam)?
  • Decision rule: \[\text{ Email x}_i\text{ is a spam }\Leftrightarrow\color{blue}{\mathbb{P}(Y_i=1|X=\text{x}_i)}\geq 0.5.\]
  • From now, building a classifier is just trying to estimate this \[\color{blue}{\mathbb{P}(Y_i=1|X=\text{x}_i)}.\]

Naive Bayes Classifiers (NBC)

Recall Bayes’s Theorem

Bayes’s Theorem

For any two events \(O,H\) with \(\mathbb{P}(O)\times\mathbb{P}(H)>0,\) \[\begin{equation}\overbrace{\mathbb{P}(H|O)}^{\text{Posterior}}=\frac{\overbrace{\mathbb{P}(O|H)}^{\text{Likelihood}}\times\overbrace{\mathbb{P}(H)}^{\text{Prior}}}{\underbrace{\mathbb{P}(O)}_{\text{Marginal}}}.\end{equation}\]

  • \(\mathbb{P}(H)\): Prior belief of having hypothesis \(H\).
  • \(\mathbb{P}(O|H)\): If \(H\) is true, how likely for \(O\) to be observed?
  • \(\mathbb{P}(H|O)\): If \(O\) is observed, how likely for \(H\) to be true?
  • \(\mathbb{P}(O)\): How likely for \(O\) to be observed in general?

Naive Bayes Classifiers (NBC)

Model Setting

  • Bayes’s theorem implies: \[\begin{align*}\color{blue}{\mathbb{P}(Y_i=1|X=\text{x}_i)}&=\frac{\color{red}{\mathbb{P}(X=\text{x}_i|Y_i=1)}\times\color{green}{\mathbb{P}(Y_i=1)}}{\mathbb{P}(X=\text{x}_i)}\\ &\propto \color{red}{\mathbb{P}(X=\text{x}_i|Y_i=1)}\times\color{green}{\mathbb{P}(Y_i=1)}.\end{align*}\]
  • \(\color{green}{\mathbb{P}(Y_i=1)}\) is easy to estimate 😊: \(\frac{\text{Number of all Spams}}{\text{Number of total emails}}\).
  • \(\color{red}{\mathbb{P}(X=\text{x}_i|Y_i=1)}\) is very complicated to estimate 🥹.

Main Assumption of Naive Bayes Classifier

Within any class \(k\in\{1,0\}\), the components of input \(X|Y=k\) are indpendent i.e., \[\color{red}{\mathbb{P}(X=\text{x}|Y=k)}=\prod_{j=1}^d\mathbb{P}(X_j=x_j|Y=k).\]

Key quantities of NBC

Key quantities in Naive Bayes

\[\mathbb{P}(Y=1|X=\text{x})\propto \color{green}{\mathbb{P}(Y=1)}\color{red}{\prod_{j=1}^d\mathbb{P}(X_j=x_j|Y=1)},\]

  • \(\mathbb{P}(X_j=x_j|Y=1)\) can be estimated (in 1D)\(^{\small\text{📚}}\) as follows:
Type of \(X_j\) Distribution Graphic
Qualitative Bernoulli, Multinomial… barplot, countplot
Quantitative Gausian, Exponential… displot, hist, density…
\(^{\text{📚}}\) Chapter 4, Introduction to Statistical Learning with R, James et al. (2021).

\(M\)-class Naive Bayes Classifier

  • For any \(d\)-dimensional input \(\text{x}\) and \(k\in\{1,2,...,M\}\):

Key quantity

\[\mathbb{P}(Y=k|X=\text{x})\propto\mathbb{P}(Y=k)\prod_{j=1}^d\mathbb{P}(X_j=x_j|Y=k).\]

Classification rule

\[x\text{ belongs to class }k^*\text{ if }\mathbb{P}(Y=k^*|X=x)=\max_{1\leq k\leq M}\mathbb{P}(Y=k|X=\text{x}).\]

Application

Application

Email type vs only 3 inputs

  • Input: \(x=(\) make, address, capitalTotal \()\in\mathbb{R}^3\).
  • Test data: the same \(20\%\) of all observations.
Code 
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.model_selection import train_test_split
sns.set(style="white")
X_train2, X_test2, y_train2, y_test2 = train_test_split(spam[["make","address", "capitalTotal"]], spam.iloc[:,57], test_size = 0.2, random_state=42)
nb2 = GaussianNB()
_, ax = plt.subplots(1,1, figsize=(3.25,3.25))
nb2 = nb2.fit(X_train2, y_train2)
pred2 = nb2.predict(X_test2)
conf2 = confusion_matrix(pred2, y_test2)
con_fig2 = ConfusionMatrixDisplay(conf2)
pr2 = nb2.predict_proba(X_test2)[:,1]
con_fig2.plot(ax=ax)
plt.show()

  • Accuracy: \[\frac{463+62}{463+62+20+297}\approx 0.624.\]
  • Misclassification error: \[1-\text{accuracy}\approx0.376.\]
  • This depends on the split ⚠️

Application

Email type vs all inputs

  • Data: \(\text{x}\in\mathbb{R}^{57},y\in\{0,1\}\).
  • Test data: the same \(20\%\).
Code 
X_train1, X_test1, y_train1, y_test1 = train_test_split(spam.iloc[:,:57], spam.iloc[:,57], test_size = 0.2, random_state=42)
_, ax = plt.subplots(1,1, figsize=(4,4))
nb1 = GaussianNB()
nb1 = nb1.fit(X_train1, y_train1)
pred1 = nb1.predict(X_test1)
conf1 = confusion_matrix(pred1, y_test1)
con_fig1 = ConfusionMatrixDisplay(conf1)
pr1 = nb1.predict_proba(X_test1)[:,1]
con_fig1.plot(ax=ax)
plt.show()

  • Accuracy: \[\frac{365+348}{365+348+11+118}\approx 0.846.\]
  • Misclassification error: \[1-\text{accuracy}\approx 0.154.\]
  • This depends on the split ⚠️

Application

Email type vs Selected Inputs

  • Visualize type against inputs can help us filter useful input features.
  • There are too many features, we can apply statistical method, for ex. ANOVA.
Code 
from scipy.stats import f_oneway
# Initialize list to store selected features
selected_features = []
p_values = {}

# Get feature column names (excluding the target)
feature_columns = [col for col in spam.columns if col != 'type']

# For loop to test each feature
for feature in feature_columns:
    # Get unique classes in target variable
    classes = spam['type'].unique()

    # Create groups for ANOVA test
    groups = []
    for class_label in classes:
        group_data = spam[spam['type'] == class_label][feature]
        groups.append(group_data)
    
    # Perform one-way ANOVA
    f_stat, p_value = f_oneway(*groups)
    
    # Store p-value
    p_values[feature] = p_value
    
    # Select feature if p-value < 1e-15
    if p_value < 1e-15:
        selected_features.append(feature)
# Create DataFrame with only selected features and target
if selected_features:
    filtered_data = spam[selected_features + ['type']]
  • Number of selected features: 38.

  • Accuracy: \[\frac{359+350}{359+350+9+124}\approx 0.842.\]
  • Misclassification error: \[1-\text{accuracy}\approx 0.158.\]
  • This depends on the split ⚠️

Pros & Cons of NBC

Pros

  • Efficiency & simplicity
  • Less training data requirement
  • Scalability: works well on large and high-dimensional data
  • Ability to handle categorical data
  • Ability to handle missing data
  • Sometimes, it still works well even thought the assumption of independence is violeted.

Cons

  • May perform poorly when features are highly correlated due to the violation of independence assumption.
  • May not work well for complex relationship.
  • Zero probability: when some categories are not presented in some training features.
  • Continuous features often be modeled using Gaussian distribution, which might not always be appropriate.

Handling Imbalanced Data

Imbalanced data ⚠️

  • If the data contains \(95\%\) nonspam, always guessing nonspam gives \(0.95\) accuracy!
  • Accuracy isn’t the right metric for imbalanced data ⚠️

Confusion Matrix


  • \(\color{purple}{\text{Precision}}=\frac{\color{CornflowerBlue}{\text{TP}}}{\color{CornflowerBlue}{\text{TP}}+\color{purple}{\text{FP}}}\)
  • \(\color{Tan}{\text{Recall}}=\frac{\color{CornflowerBlue}{\text{TP}}}{\color{CornflowerBlue}{\text{TP}}+\color{Tan}{\text{FN}}}\)
  • \(\color{ForestGreen}{\text{F1-score}}=\frac{2.\color{purple}{\text{Precision}}.\color{Tan}{\text{Recall}}}{\color{purple}{\text{Precision}}+\color{Tan}{\text{Recall}}}\).
  • \(\color{ForestGreen}{\text{F1-score}}\) balances \(\color{purple}{\text{FP}}\) & \(\color{Tan}{\text{FN}}\).

Imbalanced data ⚠️

  • \(\color{purple}{\text{Precision}}=\frac{\color{CornflowerBlue}{\text{TP}}}{\color{CornflowerBlue}{\text{TP}}+\color{purple}{\text{FP}}}\)
  • \(\color{Tan}{\text{Recall}}=\frac{\color{CornflowerBlue}{\text{TP}}}{\color{CornflowerBlue}{\text{TP}}+\color{Tan}{\text{FN}}}\)
  • \(\color{ForestGreen}{\text{F1-score}}=\frac{2.\color{purple}{\text{Precision}}.\color{Tan}{\text{Recall}}}{\color{purple}{\text{Precision}}+\color{Tan}{\text{Recall}}}\).
Code 
import plotly.graph_objects as go
x = np.linspace(0,1,20)
y = np.linspace(0,1,20)
z1 = [[2*x[i]*y[j]/(x[i]+y[j]) for j in range(len(y))] for i in range(len(x))]
z2 = [[(x[i]+y[j])/2 for j in range(len(y))] for i in range(len(x))]

camera = dict(
    eye=dict(x=1.7, y=-1.2, z=1.2)
)

fig = go.Figure(go.Surface(x = x,
                           y = y,
                           z = z1,
                           name = "F1-score",
                           colorscale = "Blues",
                           showscale = False))
fig.add_trace(go.Surface(x = x,
                         y = y,
                         z = z2,
                        name = "Mean",
                        colorscale = "Electric",
                        showscale = False))
fig.update_layout(scene = dict(
                    xaxis_title='Precision',
                    yaxis_title='Recall',
                    zaxis_title='Scores'),
                  title = dict(text="F1-score vs Mean", 
                               y=0.9,
                               x=0.5,
                               font=dict(size = 30, 
                                         color = "#1C66B5")
                              ),
                  scene_camera=camera,
                  width = 560,
                  height = 500)
fig.show()

Imbalanced data ⚠️

Receiver Operating Characteristic Curve (ROC)

\(\bullet\) ROC \(=\{(\)FPR\(_{\delta}\),TPR\(_{\delta}):\delta\in[0,1]\}\).
\(\bullet\) Better model = Larger Area Under the Curve (AUC).

Code 
from plot_metric.functions import BinaryClassification
from plotly.tools import mpl_to_plotly
# Visualisation with plot_metric
y1 = 1*(y_test1 == "spam")
bc1 = BinaryClassification(y1, pr1, labels=["nonspam", "spam"], seaborn_style="whitegrid")

bc2 = BinaryClassification(y1, pr2, labels=["nonspam", "spam"], seaborn_style="whitegrid")

# Figures
a = bc1.plot_roc_curve()
fig_full = plt.gcf()
pl_full = mpl_to_plotly(fig_full)
pl_full.update_layout(width=500, height=450, 
                      title=dict(text="ROC Curve of Full model", 
                                 font=dict(size=25)),
                      xaxis_title = dict(font=dict(size=20, color = "red")),
                      yaxis_title = dict(text='True Positive Rate (Recall)', font=dict(size=20, color = "#EBB31D")),
                      template='plotly_white')
pl_full.show()

Imbalanced data ⚠️

Receiver Operating Characteristic Curve (ROC)

\(\bullet\) ROC \(=\{(\)FPR\(_{\delta}\),TPR\(_{\delta}):\delta\in[0,1]\}\).
\(\bullet\) Better model = Larger Area Under the Curve (AUC).

Code 
bc2 = BinaryClassification(y1, pr2, labels=["nonspam", "spam"], seaborn_style="whitegrid")

# Figures
b = bc2.plot_roc_curve()
fig_3 = plt.gcf()
pl_3 = mpl_to_plotly(fig_3)
pl_3.update_layout(width=500, height=450, 
                      title=dict(text="ROC Curve of 3-input model", 
                                 font=dict(size=25)),
                      xaxis_title = dict(font=dict(size=20, color = "red")),
                      yaxis_title = dict(text='True Positive Rate (Recall)', font=dict(size=20, color = "#EBB31D")),
                      template='plotly_white')
pl_3.show()

Imbalanced data ⚠️ (Summary)

Confusion matrix

  • Precision: controlls FP.
  • Recall: controlls FN.
  • F1-score: ballances the two.

ROC Curve & AUC

  • ROC Curve: ballances TPR and FPR.
  • Can be used to select \(\delta\in [0,1]\).
  • Better model = Larger AUC.

Imbalanced data ⚠️ (to explore)

  • Sampling methods:
    • Oversampling: random, SMOTE, SMOTE SVM, ADASYN…
    • Undersampling: random, new miss, CNN, Tomek Links…
  • Weight adjustment methods (nonparametric)
    • Tree-based algorithms, \(k\)-NN, kernel methods…
  • Tuning threshold \(\delta\).
  • Work with packages that handle imbalanced data:
  • Helpful links: Geeks for Geeks, Angelleon Collado, Machine Learning Mastery…

2. Logistic Regression

Binary Logistic Regression

Binary Logistic Regression

Model setting

x1 x2 y
-0.752759 2.704286 1
1.935603 -0.838856 0
Code 
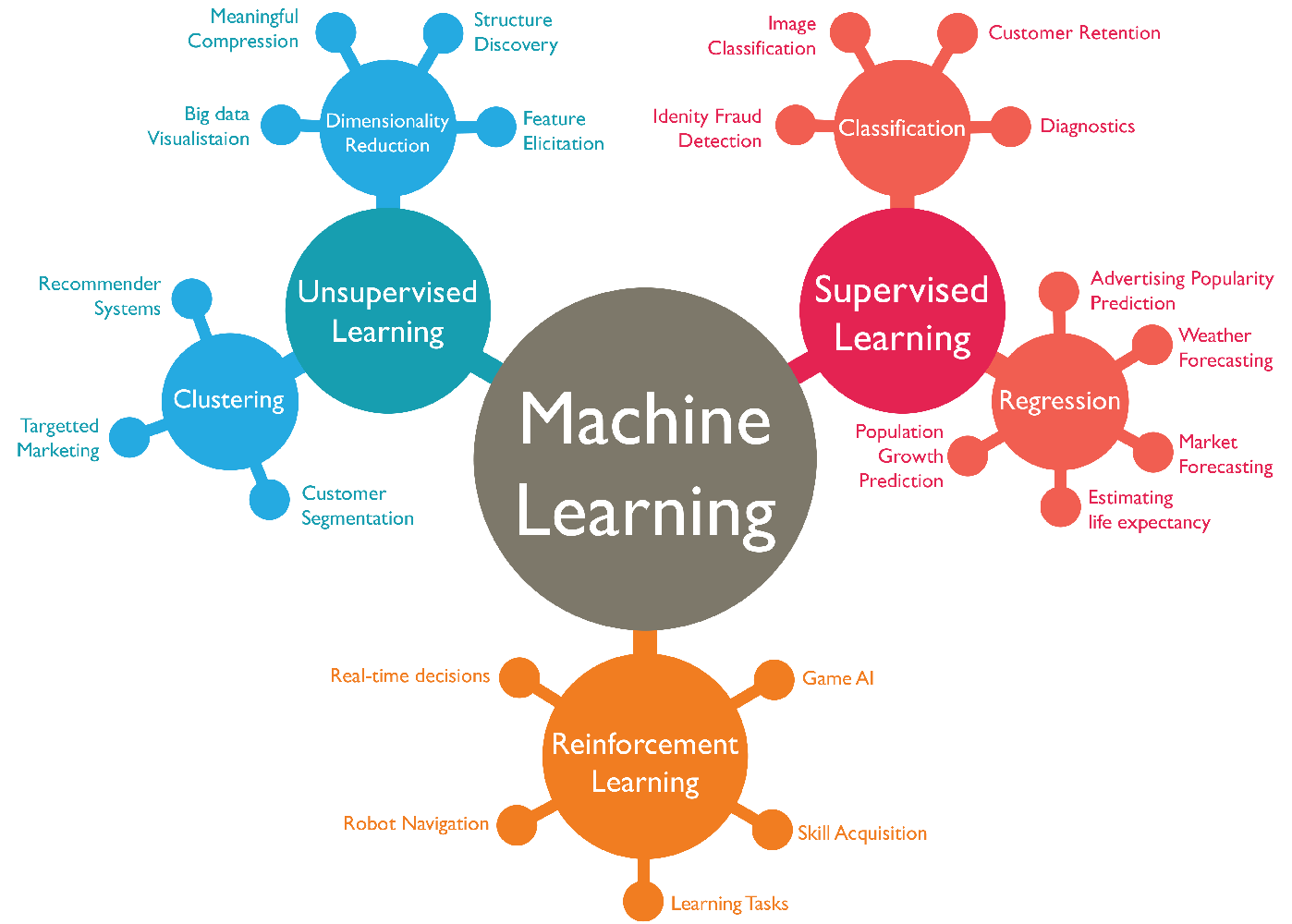
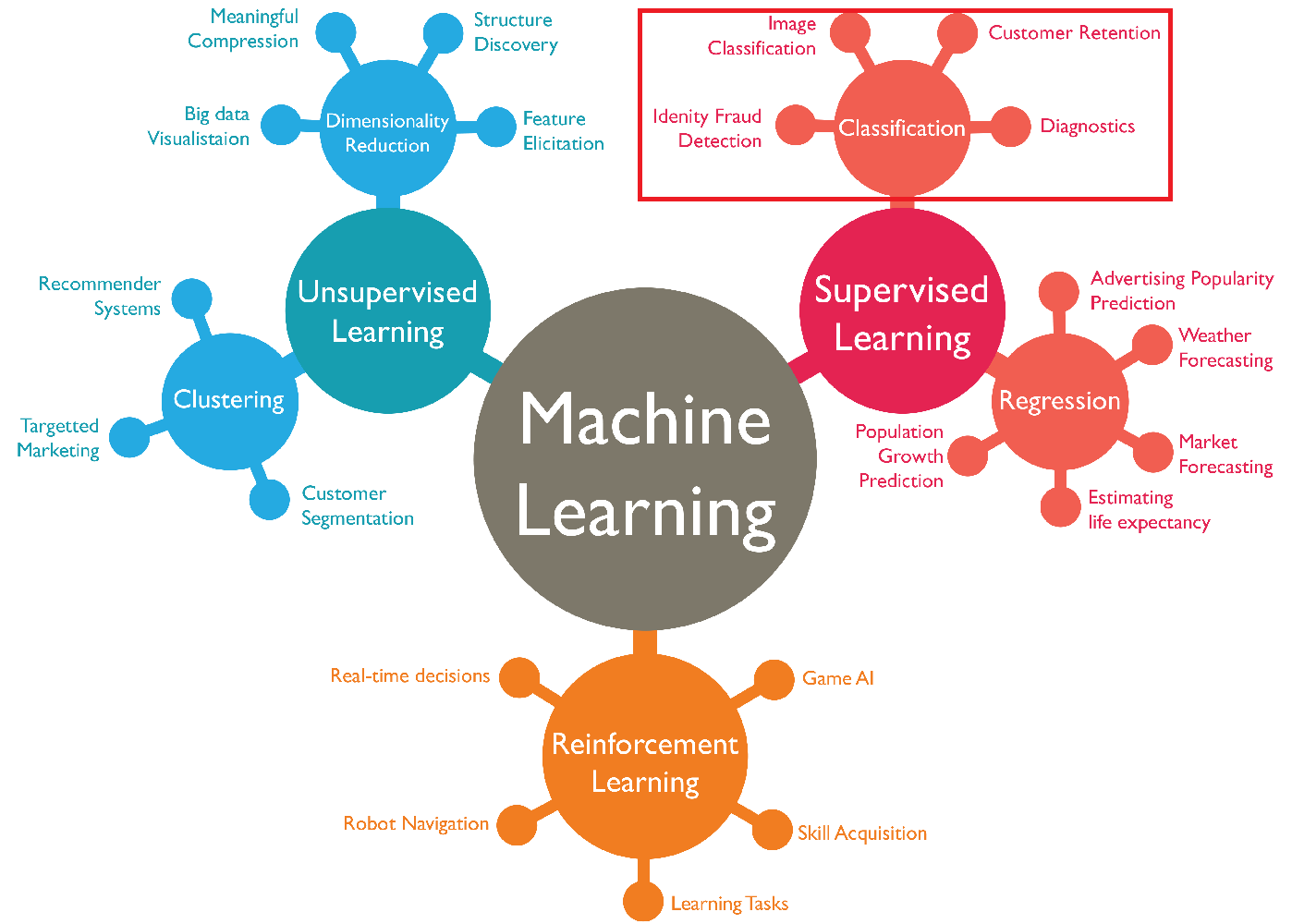
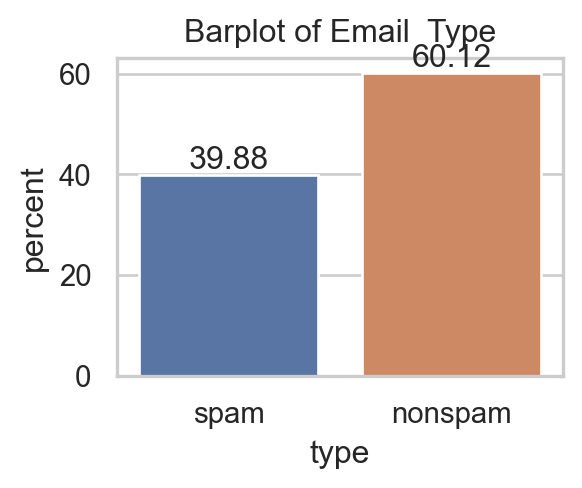
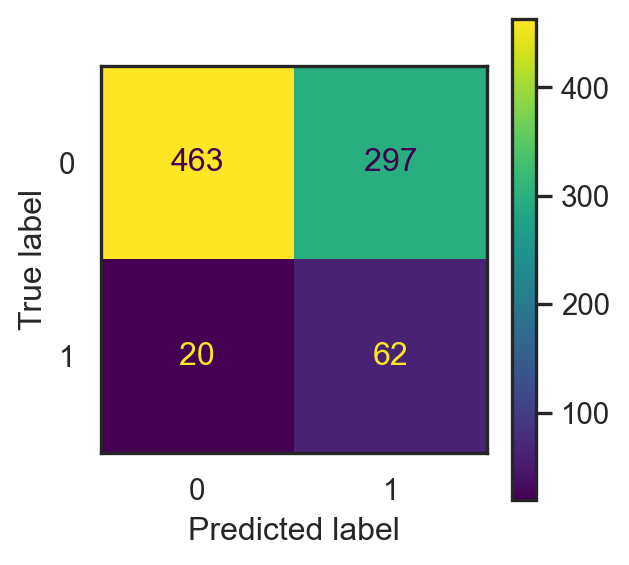
import plotly.express as px
import plotly.graph_objects as go
fig = px.scatter(
    data_toy1, x="x1", y="x2", 
    color="y")

# Lines
line_coefs = np.array(
    [[1, 1, -2], [-1, 0.3, 0.5], [-0.5, 0.3, -1], [0.1, -1, 1]])
frames = []
x_line = np.array([np.min(x1[:,1]), np.max(x1[:,1])])
y_range = np.array([np.min(x1[:,2]), np.max(x1[:,2])])
id_small = np.argsort(np.abs(x1[:,1]) + np.abs(x1[:,2]))[5]
point_far = np.array([x_line[0], y_range[1]])
point_near = np.array([x1[id_small,1],x1[id_small,2]])

for i, coef in enumerate(line_coefs):
    y_line = (-coef[0] - coef[1] * x_line) / coef[2]
    a, b = -coef[1]/coef[2], -coef[0]/coef[2]
    point_proj_far = np.array([(point_far[0]+a*point_far[1]-a*b)/(a**2+1), a*(point_far[0]+a*point_far[1]-a*b)/(a**2+1)+b])
    point_proj_near = np.array([(point_near[0]+a*point_near[1]-a*b)/(a**2+1), a*(point_near[0]+a*point_near[1]-a*b)/(a**2+1)+b])
    p1 = np.row_stack([point_far, point_proj_far])
    p2 = np.row_stack([point_near, point_proj_near])
    frames.append(go.Frame(
        data=[fig.data[0],
              fig.data[1],
              go.Scatter(
                x=p1[:,0],
                y=p1[:,1],
                name="Far from boundary",
                line=dict(dash="dash"),
                visible="legendonly"
              ),
              go.Scatter(
                x=p2[:,0],
                y=p2[:,1],
                name="Close to boundary",
                line=dict(dash="dash"),
                visible="legendonly"
              ),
              go.Scatter(
                x=x_line, y=y_line, mode='lines',
                line=dict(width=3, color="black"), 
                name=f'Line: {i+1}')],
        name=f'{i+1}'))

y_line = (-line_coefs[0,0] - line_coefs[0,1] * x_line) / line_coefs[0,2]
a, b = -line_coefs[0,0]/line_coefs[0,2], - line_coefs[0,1]/line_coefs[0,2]
point_proj_far = np.array([(point_far[0]+a*point_far[1]-a*b)/(a**2+1), a*(point_far[0]+a*point_far[1]-a*b)/(a**2+1)+b])
point_proj_near = np.array([(point_near[0]+a*point_near[1]-a*b)/(a**2+1), a*(point_near[0]+a*point_near[1]-a*b)/(a**2+1)+b])
p1 = np.row_stack([point_far, point_proj_far])
p2 = np.row_stack([point_near, point_proj_near])
fig1 = go.Figure(
    data=[
        fig.data[0],
        fig.data[1],
        go.Scatter(
            x=p1[:,0],
            y=p1[:,1],
            name="Far from boundary",
            line=dict(dash="dash"),
            visible="legendonly"
            ),
        go.Scatter(
            x=p2[:,0],
            y=p2[:,1],
            name="Close to boundary",
            line=dict(dash="dash"),
            visible="legendonly"
        ),
        go.Scatter(
            x=x_line, y=y_line, mode='lines',
            line=dict(width=3, color="black"), 
            name=f'Line: 1')
    ],
    layout=go.Layout(
        title="1st simulated data & boundary lines",
        xaxis=dict(title="x1", range=[-3.4, 3.4]),
        yaxis=dict(title="x2", range=[-3.4, 3.4]),
        updatemenus=[{
            "buttons": [
                {
                    "args": [None, {"frame": {"duration": 1000, "redraw": True}, "fromcurrent": True, "mode": "immediate"}],
                    "label": "Play",
                    "method": "animate"
                },
                {
                    "args": [[None], {"frame": {"duration": 0, "redraw": False}, "mode": "immediate"}],
                    "label": "Stop",
                    "method": "animate"
                }
            ],
            "type": "buttons",
            "showactive": False,
            "x": -0.1,
            "y": 1.25,
            "pad": {"r": 10, "t": 50}
        }],
        sliders=[{
            "active": 0,
            "currentvalue": {"prefix": "Line: "},
            "pad": {"t": 50},
            "steps": [{"label": f"{i}",
                       "method": "animate",
                       "args": [[f'{i}'], {"frame": {"duration": 1000, "redraw": True}, "mode": "immediate", 
                       "transition": {"duration": 10}}]}
                      for i in range(1,5)]
        }]
    ),
    frames=frames
)

fig1.update_layout(height=370, width=500)

fig1.show()
  • Objective: Given input \(\text{x}_i\in\mathbb{R}^d\), classify if \(y\in\{0,1\}\) (Male or female).
  • Main idea: classify \(\Leftrightarrow\) identify decision boundary.
  • Main assumption: Boundary(B) is linear.
  • Model: Given input \(\text{x}_i\), the chance that it belongs to class \(1\) is given by \[\mathbb{P}(Y_i=1|X=\text{x}_i)=\sigma(\color{blue}{\beta_0}+\sum_{j=1}^d\color{blue}{\beta_j}x_{ij}),\] where \(\color{blue}{\beta_0,\beta_1,\dots,\beta_d}\in\mathbb{R}\) are the key parameters to be estiamted from the data, and \(\sigma(t)=1/(1+e^{-t}),\forall t\geq 0\).

Binary Logistic Regression

Model intuition

  • Ex: Given \(\text{x}_0=[\text{h}_0,\text{w}_0]\in\mathbb{R}^2,\) for any candidate parameter \(\color{blue}{\vec{\beta}=[\beta_0,\beta_1,\beta_2]}\), \[\color{green}{z_0}=\color{blue}{\beta_0}+\color{blue}{\beta_1}\text{h}_0+\color{blue}{\beta_2}\text{w}_0\text{ is the relative distance from }\text{x}_0\to\text{ Boundary (B)}.\]
  • That’s to say that
    • \(\color{green}{z_0}>0\Leftrightarrow \text{x}_0\) is above the boundary.
    • \(|\color{green}{z_0}|\) is large \(\Leftrightarrow\) \(\text{x}_0\) is far from the bounday.
  • A good boundary should be such that:
    • \(|\color{green}{z_0}|\) large \(\Rightarrow\) “certain about its class”.
    • \(|\color{green}{z_0}|\) small \(\Rightarrow\) “less certain about its class”.

Binary Logistic Regression

Model intuition

  • A good boundary should be such that:
    • \(|\color{green}{z_0}|\) large \(\Rightarrow\) “certain about its class”.
    • \(|\color{green}{z_0}|\) small \(\Rightarrow\) “less certain about its class”.
  • Sigmoid function, \(\sigma:\mathbb{R}\to (0,1)\)

\[\color{green}{z}\mapsto\sigma(\color{green}{z})=\frac{1}{1+\exp(-\color{green}{z})}.\]

Key ideas

  • \(\color{green}{z_0}=\color{blue}{\beta_0}+\text{x}_0^T\color{blue}{\vec{\beta}}\) is the relative distance of \(\text{x}_0\) w.r.t (B).
  • Sigmoid converts this relative distance into probability.

Binary Logistic Regression

Example

  • For \(\color{blue}{(\beta_0,\beta_1,\beta_2)=(1, 1, -2)}\), compute \(p(\color{blue}{1}|\text{x})\) for the data:
x1 x2 y
2.489186 -0.779048 0
-2.572868 -1.086146 1
2.767143 2.432104 0

  • Compute relative distance \(z_i=\color{blue}{\beta_0}+\text{x}_i^T\color{blue}{\vec{\beta}}\), then \(p(1|\text{x}_i)\) \[\begin{align*}z_1&=1+1(2.489186)-2(-0.779048)\\ &=5.047282>0\\ \Rightarrow p(1|\text{x}_1)&=\sigma(z_1)=1/(1+e^{-5.047282})=\color{blue}{0.9936}.\\ \\ z_2&=1+1(-2.572868)-2(-1.086146)\\ &=0.599424>0\\ \Rightarrow p(1|\text{x}_2)&=\sigma(z_2)=1/(1+e^{-0.599424})=\color{blue}{0.6455}.\\ \\ z_3&=1+1(2.767143)-2(2.432104)\\ &=-1.097065 < 0\\ \Rightarrow p(1|\text{x}_3)&=\sigma(z_3)=1/(1+e^{-(-1.097065)})=\color{red}{0.2503}.\end{align*}\]

  • Interpretation: \(\text{x}_1,\text{x}_2\) are located above the line \((B):1+x_1-2x_2\) as \(z_1,z_2>0\) and are predicted to be in class \(\color{blue}{1}\). On the other hand, \(\text{x}_3\) is located below the line (\(z_3<0\)) and is predicted to be in class \(\color{red}{0}\).

  • Q4: Now,how do we find the best key parameter \(\color{blue}{\beta_0,\dots,\beta_d}\)?

  • We will build a criterion just like RSS in linear regression.

Conditional Likelihood and Loss Function

Binary Logistic Regression

Conditional likelihood \(\to\) Cross-entropy

  • Data: \({\cal D}=\{(\text{x}_1,y_1),...,(\text{x}_n,y_n)\}\subset\mathbb{R}^d\times \{0,1\}\).
  • Objective: search for \(\color{blue}{\beta_0}\in\mathbb{R},\color{blue}{\vec{\beta}}\in\mathbb{R}^d\) such that the model is best aligned with the data \({\cal D}\): \[p(y_i|\text{x}_i)\text{ is large for all }i\in\{1,\dots,n\}.\]

  • Conditional Likelihood Function: If the data are iid, one has \[\begin{align*}{L}(\color{blue}{\beta_0},\color{blue}{\vec{\beta}})&=\mathbb{P}(Y_1=y_1,\dots,Y_n=y_n|X_1=\text{x}_1,\dots,X_n=\text{x}_n)\\ &=\prod_{i=1}^np(y_i|\text{x}_i)\\ &=\prod_{i=1}^n\Big[p(1|\text{x}_i)\Big]^{y_i}\Big[p(0|\text{x}_i)\Big]^{1-y_i}\\ &=\prod_{i=1}^n\Big[\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}})\Big]^{y_i}\Big[(1-\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}}))\Big]^{1-y_i}. \end{align*}\]

  • Cross-entropy: \(\text{CEn}(\color{blue}{\vec{\beta}})=-\sum_{i=1}^n\Big[y_i\log[\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}})]+(1-y_i)\log[(1-\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}}))]\Big]\).

Binary Logistic Regression

Conditional likelihood \(\to\) Cross-entropy

  • Cross-entropy: \(\text{CEn}(\color{blue}{\vec{\beta}})=-\sum_{i=1}^n\Big[y_i\log[\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}})]+(1-y_i)\log[(1-\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}}))]\Big]\).
  • It’s also known as log-loss or logistic loss.
Code 
def log_loss(beta1, beta2, X, y, beta0 = 0.1):
    beta_ = np.array([beta0, beta1, beta2])
    sig = sigmoid(X @ beta_)
    loss = np.mean(y*np.log(sig) + (1-y)*np.log(1-sig))
    return -loss

beta1 = np.linspace(-7,2,25)
beta2 = np.linspace(-2,7,30)
losses = np.array([[log_loss(b1, b2, X=x1, y=y_) for b1 in beta1] for b2 in beta2])
bright_blue1 = [[0, '#235b63'], [1, '#45e696']]
fig = go.Figure(go.Surface(
    x=beta1, y=beta2, z=losses, name="Loss function",
    colorscale=bright_blue1,
    hovertemplate='beta1: %{x}<br>' + 
                  'beta2: %{y}<br>' +
                  'Loss: %{z}<extra></extra>'))
fig.update_layout(
                scene = dict(
                xaxis_title= 'beta1',
                yaxis_title= 'beta2',
                zaxis_title='Loss'),
                width=800, height=300, title="Loss function of the simulated dataset")
fig.show()

Binary Logistic Regression

Estimating coefficients

  • We search for coefficient \(\color{blue}{\vec{\beta}}=[\color{blue}{\beta_0,\dots,\beta_d}]\) minimizing \[\text{CEn}(\color{blue}{\vec{\beta}})=-\sum_{i=1}^n\Big[y_i\log[\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}})]+(1-y_i)\log[(1-\sigma(-\color{blue}{\beta_0}-\text{x}_i^T\color{blue}{\vec{\beta}}))]\Big].\]

  • 😭 Unfortunately, such minimizer values \((\color{blue}{\widehat{\beta}_0,\widehat{\vec{\beta}}})\) CANNOT be analytically computed.

  • 😊 Fortunately, it can be numerically approximated!

  • We can use optimization algorithms such as Gradient Descent Algorithm to estimate the best \(\color{blue}{\hat{\beta}}\).

  • This is the next step!

Binary Logistic Regression

Summary

Logistic Regression Model

  • Main model: \(p(1|\text{x})=1/(1+e^{-\color{green}{z}})=1/(1+e^{-(\color{blue}{\beta_0}+\text{x}^T\color{blue}{\vec{\beta}})})\).
    • Interpretation:
      • Boundary decision is Linear defined by the coefficients \(\color{blue}{\beta_0}\) and \(\color{blue}{\vec{\beta}}\).
      • Probability of being in each class depends on the relative distance of that point to the boundary.
      • Works well when classes are linearly separable.

  • Objective: buliding a Logistic Regression model is equivalent to searching for parameters \(\color{blue}{\beta_0}\) and \(\color{blue}{\vec{\beta}}\) that minimizes the Cross-entropy.
  • The loss cannot be minimized analytically but can be minimized numerically.

Optimization: GD & SGD

Binary Logistic Regression

Gradient

  • If \(L:\mathbb{R}^d\to\mathbb{R}, y=L(x_1,...,x_d)\) be a real-valued function of \(d\) real variables. For any point \(a\in\mathbb{R}^d\), the gradient of \(L\) at point \(a\) is a \(d\)-dimensional vector defined by \[\nabla L(a)=\begin{bmatrix}\frac{\partial L}{\partial x_1}(a)\\ \vdots\\ \frac{\partial L}{\partial x_d}(a)\end{bmatrix}.\]
  • It is the direction (from the point \(a\)) with the fastest increasing rate of the function \(L\).
  • Ex: \(f(x,y)=0.1x^4+0.5y^2\). Compute \(\nabla f(1,-1)\).
    • One has \(\frac{\partial f}{\partial x}=0.4x^3\) and \(\frac{\partial f}{\partial y}=y\).
    • Therefore, \(\nabla f(1,-1)=(0.4,-1).\)
    • Meaning: from point \((1,-1)\), function \(f\) increases fastest along the direction \((0.4, -1)\).
  • Around 1847, Augustin-Louis Cauchy used this to propose a genius algorithm that makes impossibilities, possible!



Binary Logistic Regression

Gradient Descent Algorithm (GD)

  • If \(L\) is the loss function, then our goal is to find its lowest position.
  • Consider \(\theta_0\in\mathbb{R}^d\) and if \(L\) is differentiable, we can approximate \(L\) by a linear form around \(\theta_0\): \[L(\color{green}{\theta_0+h})\approx L(\color{red}{\theta_0})+\nabla L(\theta_0)^Th.\]
    • If \(h=-\eta\nabla L(\theta_0)\) for some \(\eta>0\), we have: \(L(\color{green}{\theta_0-\eta\nabla L(\theta_0)})\approx L(\color{red}{\theta_0})-\eta\|\nabla L(\theta_0)\|^2\leq L(\theta_0).\)
    • Interpretation: The loss \(L(\color{green}{\theta_0-\eta\nabla L(\theta_0)})\) is likely to be lower than \(L(\color{red}{\theta_0})\), therefore in searching for the lowest positoin of \(L\), we should move from \(\color{red}{\theta_0}\to\color{green}{\theta_0-\eta\nabla L(\theta_0)}\). This is the main idea of GD algorithm.
  • Gradient Descent Algorithm:
    • Initialiaztion:
      • learning rate: \(\eta>0\) (small \(\approx 0.001\) or \(0.01\))
      • initial value: \(\theta_0\)
      • Maximum iteration: \(N\)
      • Stopping threshold: \(\delta>0\) (small \(< 10^{-5}\)).
    • Update: for t=1,2,...,N: \[\color{green}{\theta_{t}:=\theta_{t-1}-\eta\nabla L(\theta_{t-1})}.\]
      • if \(\|\nabla L(\theta_{t^*})\|<\delta\) at some step \(t^*\): return \(\color{green}{\theta_{t^*}}\).
      • else: return \(\color{green}{\theta_{N}}\).

Binary Logistic Regression

Gradient Descent Algorithm (GD)

Binary Logistic Regression

Stochastic Gradient Descent (SGD)

Stochastic Gradient Descent (SGD) Algorithm

  • Recall that for Logistic Regression, log loss is defined by \[\color{red}{{\cal L}(\beta_0,\vec{\beta})}=-\color{red}{\sum_{i=1}^n}\left[y_i\log(p(1|\text{x}_i))+(1-y_i)\log(p(0|\text{x}_i))\right]:=\color{red}{\sum_{i=1}^n}\ell(y_i,\hat{y}_i).\]
  • In GD, the gradient \(\nabla {\cal L}\) is computed using the whole training data, which is very costly for large datasets.
  • Using statistics, at each iteration \(t=1,\dots,N\), we can approximate \(\color{red}{\sum_{i=1}^n}\) in the loss by \(\color{green}{\sum_{i\in B_t}}\) using some random subset \(B_t\subset \{1,\dots,n\}\) (called minibatch), i.e., \(\color{red}{{\cal L}(\beta_0,\vec{\beta})}\approx\color{green}{\widehat{\cal L}(\beta_0,\vec{\beta})}=\color{green}{\sum_{i\in B_t}}\ell(y_i,\hat{y}_i)\).
  • Stochastic Gradient Descent Algorithm: (In Logistic Regression: \(\theta=(\beta_0,\vec{\beta})\))
    • Initialize: \(\eta, N, \theta_0, \delta>0\) (same as in GD), and minibatch size \(b=|B_t|,\forall t=1,2,...,N\).
    • Main loop: for i=1,2,...,N: \[\color{green}{\theta_{t}}:=\color{red}{\theta_{t-1}}+\eta\nabla\color{green}{\widehat{\cal L}}(\color{red}{\theta_{t-1}}).\]
  • Ex: Consider 1st simuated data 👉

Binary Logistic Regression

Stochastic Gradient Descent (SGD) in Action

Binary Logistic Regression

Gradient of Log Loss

Optimizing Log Loss in Logistic Regression

  • Log loss for any parameter \(\beta_0,\vec{\beta}\in\mathbb{R}^d: {\cal L}(\beta_0,\vec{\beta})=-\sum_{i=1}^n[y_i\log(p(1|\text{x}_i))+(1-y_i)\log(p(0|\text{x}_i))]\).
  • You should verify that:
    • \(\partial_{\beta_0} {\cal L}(\beta_0,\vec{\beta})=\sum_{i=1}^n\partial_{\beta_0} \ell(y_i,\hat{y}_i)=-\sum_{i=1}^n(y_i-p(1|\text{x}_i))\in\mathbb{R}\).
    • \(\nabla_{\vec{\beta}} {\cal L}(\beta_0,\vec{\beta})=\sum_{i=1}^n\nabla_{\vec{\beta}} \ell(y_i,\hat{y}_i)=-\sum_{i=1}^n\underbrace{(y_i-p(1|\text{x}_i))}_{\in\mathbb{R}}\underbrace{\text{x}_i}_{\in\mathbb{R}^d}\).
  • We define sigmoid function \(\sigma\) and the above gradient function of log loss as follow:
def sigmoid(z):
    return 1/(1+np.exp(-z))

def gradLogLoss(beta, X,y):
    X_ = np.column_stack([np.ones_like(y), np.array(X)])
    return -np.sum(np.diag(y-sigmoid(X_ @ beta)) @ X_, axis=0)

  • GD code is given in the next panel.

  • SGD can be implemented easily from this GD code.

d = 3 # input dimension of X
def grad_desc(grad, X, y, theta0 = [0]*(d+1), 
              max_Iter = 100, lr = 0.1, threshold = 1e-10):
    if theta0 is None:
        val = [np.random.uniform(-10, 10, size=d)]
    else:
        val = [np.array(theta0)]
    grads = [grad(theta0, X, y)]
    for i in range(max_Iter):
        if np.sum(np.abs(grads[-1])) < threshold:
            return np.row_stack(val), np.row_stack(grads)
        new = val[-1] - lr * grads[-1]
        val.append(new)
        gr = grad(new)
        grads.append(gr)
    return np.row_stack(val), np.row_stack(grads)

Binary Logistic Regression

More about gradient-based optimizations

Binary Logistic Regression

Application on Spam dataset

  • We build Binary Logistic Regression for spam filtering.
  • The same \(20%\) test data is considered.
  • Feature engineering:
    • Standardization features: \[x_j\to\tilde{x}_j=\frac{x_j-\mu_j}{\sigma_j}.\]
  • Standardization often helps the optimization to converge faster.
Code 
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
# Standardization
scaler = StandardScaler()
X_sc_train = scaler.fit_transform(X_train1)
X_sc_test = scaler.transform(X_test1)

# Fit model
logit = LogisticRegression()
logit = logit.fit(X_sc_train, y_train1)
logit_pred = logit.predict(X_sc_test)
logit_pred_pro = logit.predict_proba(X_sc_test)[:,1]
acc = np.mean(logit_pred.flatten() == y_test1.to_numpy().flatten())
sns.set(style="white")
_, ax = plt.subplots(1,1,figsize=(3.5,1.5))
conf = confusion_matrix(logit_pred, y_test1)
con_fig = ConfusionMatrixDisplay(conf)
con_fig.plot(ax=ax)
ax.set_title(f"Accuracy = {np.round(acc,3)}")
plt.show()

Binary Logistic Regression

Summary

  • We introduce basic concept of Logistic Regression Model: \[p(1|X=\text{x})=\frac{1}{(1+e^{-\color{blue}{\beta_0}-\text{x}^T\color{blue}{\vec{\beta}}})}.\]
  • The intuition of the model: the probability of being in class \(1\) depends on the relative distance from \(\text{x}\) to a linear boundary defined by \(\color{blue}{[\beta_0,\beta_1,\dots,\beta_d]}\).
  • The linear boundary assumption may be too weak in practice.
  • The performance of the model can be improved further by
    • Selecting relevant features
    • Feature engineering: polynomial transform…
    • Regularization or penalty methods…

Multinomial Logistic Regression

Multinomial Logistic Regression

Model

  • In this case, \(y\) takes \(M\) distinct values, it’s often encoded to be \(M\)-dimensional vector: \[y=k\Leftrightarrow p=(0,\dots,0,\underbrace{1}_{k\text{th index}},0,\dots,0)^T.\]
  • The model also returns \(M\)-dimensional probability vector where index with highest probability is the predicted class.
  • \(\text{Softmax}:\mathbb{R}^M\to\mathbb{S}_{M-1}=\{p_j\in[0,1]^M:\sum_{j=1}^Mp_j=1\}\) defined by \[\vec{z}\mapsto \vec{s}=\text{Softmax}(z)=\Big(\frac{e^{z_1}}{\sum_{j=1}^Me^{z_j}},\dots,\frac{e^{z_M}}{\sum_{j=1}^Me^{z_j}}\Big).\]
  • It converts any \(M\)-dimensional vector \(\vec{z}\) to \(M\)-dimensional probability vector \(\vec{s}\).

Multinomial Logistic Regression

Model

  • \(\text{Softmax}:\mathbb{R}^M\to\mathbb{S}_{M-1}=\{p_j\in[0,1]^M:\sum_{j=1}^Mp_j=1\}\) defined by \[\vec{z}\mapsto \vec{s}=\text{Softmax}(z)=\Big(\frac{e^{z_1}}{\sum_{j=1}^Me^{z_j}},\dots,\frac{e^{z_M}}{\sum_{j=1}^Me^{z_j}}\Big).\]
  • Model: Given parameter matrix \(\color{green}{W}\) of size \(M\times d\) and intercept vector \(\color{green}{\vec{b}}\in\mathbb{R}^d\), the predicted probability of any input data \(\text{x}_i\in\mathbb{R}^d\) is defined by

\[\begin{align*}\color{red}{\hat{p}_i}&=\text{Softmax}(\color{green}{W}\text{x}_i+\color{green}{\vec{b}})\\ &=\text{Softmax}\begin{pmatrix} \color{green}{\begin{bmatrix}w_{11}& \dots & w_{1d}\\ w_{11}& \dots & w_{1d}\\ \vdots & \vdots & \vdots\\ w_{M1}& \dots & w_{Md}\end{bmatrix}}\begin{bmatrix}x_{i1}\\ x_{i2}\\ \vdots\\ x_{id}\end{bmatrix}+\color{green}{\begin{bmatrix}b_{1}\\ b_{2}\\ \vdots\\ b_{M}\end{bmatrix}}\end{pmatrix}=\color{red}{\begin{bmatrix}p_{i1}\\ p_{i2}\\ \vdots\\ p_{iM}\end{bmatrix}}\end{align*}\]

Multinomial Logistic Regression

Model

\[\begin{align*}\color{red}{\hat{p}_i}&=\text{Softmax}(\color{green}{W}\text{x}_i+\color{green}{\vec{b}})\\ &=\text{Softmax}\begin{pmatrix} \color{green}{\begin{bmatrix}w_{11}& \dots & w_{1d}\\ w_{11}& \dots & w_{1d}\\ \vdots & \vdots & \vdots\\ w_{M1}& \dots & w_{Md}\end{bmatrix}}\begin{bmatrix}x_{i1}\\ x_{i2}\\ \vdots\\ x_{id}\end{bmatrix}+\color{green}{\begin{bmatrix}b_{1}\\ b_{2}\\ \vdots\\ b_{M}\end{bmatrix}}\end{pmatrix}=\color{red}{\begin{bmatrix}p_{i1}\\ p_{i2}\\ \vdots\\ p_{iM}\end{bmatrix}}\end{align*}\]

Multinomial Logistic Regression

Cross-entropy loss

  • We search for best possible parameters \(\color{green}{W}\in\mathbb{R}^{M\times d}\) and \(\color{green}{\vec{b}}\in\mathbb{R}^d\) by minimizing Cross Entropy loss defined below: \[\text{CEn}(W,\vec{b})=-\sum_{i=1}^n\sum_{m=1}^M\color{blue}{p_{im}}\log(\color{red}{\hat{p}_{im}}),\text{ where }\color{red}{\widehat{\text{p}}_i}=(\color{red}{\hat{p}_{i1}},\color{red}{\dots},\color{red}{\hat{p}_{iM}})\text{ is the predicted probability of }\color{blue}{\text{p}_i}.\]

Multinomial Logistic Regression

Gradient of Cross-Entropy

Optimizing Cross-entropy in Multinomial Logistic Regression

  • Cross Entropy of any parameter \(\color{green}{W}\in\mathbb{R}^{M\times d}\) and \(\color{green}{\vec{b}}\in\mathbb{R}^d\): \(\text{CEn}(\color{green}{W},\color{green}{\vec{b}})=-\sum_{i=1}^n\sum_{m=1}^M\color{blue}{p_{im}}\log(\color{red}{\widehat{p}_{im}})\).
  • Challenge: Show that
    • \(\nabla_{\color{green}{\vec{b}}} \text{CEn}(\color{green}{W},\color{green}{\vec{b}})=\sum_{i=1}^n\nabla_{\color{green}{\vec{b}}} \ell(\color{blue}{\text{p}_i},\color{red}{\hat{\text{p}}_i})=-\sum_{i=1}^n\underbrace{(\color{blue}{\text{p}_i}-\text{softmax}(\color{green}{W}\text{x}+\color{green}{\vec{b}}))}_{\in\mathbb{R}^d}\).
    • \(\nabla_{\color{green}{W}} \text{CEn}(\color{green}{W},\color{green}{\vec{b}})=\sum_{i=1}^n\nabla_{\color{green}{W}} \ell(\color{blue}{\text{p}_i},\color{red}{\widehat{p}_i})=-\sum_{i=1}^n\underbrace{(\color{blue}{\text{p}_i}-\color{red}{\widehat{\text{p}}_i})}_{\in\mathbb{R}^{d\times 1}}\underbrace{\text{x}_i^T}_{\in\mathbb{R}^{1\times d}}=\underbrace{(\color{red}{\widehat{P}}-\color{blue}{P})^TX}_{\in\mathbb{R}^{d\times d}}\), where

\[\begin{align*} \color{red}{\hat{P}}=\color{red}{\underbrace{\begin{bmatrix} \hat{p}_{11} &\dots & \hat{p}_{1d}\\ \vdots & \vdots & \vdots\\ \hat{p}_{n1} &\dots & \hat{p}_{nd} \end{bmatrix}}_{\text{Matrix of predicted probab}}}, \color{blue}{P}=\color{blue}{\underbrace{\begin{bmatrix} p_{11} &\dots & p_{1d}\\ \vdots & \vdots & \vdots\\ p_{n1} &\dots & p_{nd} \end{bmatrix}}_{\text{One-hot encoded matrix of $y_i$}}}\text{ and } X=\underbrace{\begin{bmatrix} x_{11} &\dots & x_{1d}\\ \vdots & \vdots & \vdots\\ x_{n1} &\dots & x_{nd} \end{bmatrix}}_{\text{Matrix of inputs $x_i$}} \end{align*}\]

Further reading: J. Chiang (2023) and K. Stratos (2018).

Multinomial Logistic Regression

Pros & Cons

Pros

  • Simplicity: It’s easy to understand and implement.
  • Efficiency: It’s not so computationally expensive, making it suitable for large datasets.
  • Interpretability: It converts relative distances from input data to boundary decision into probabilities, which can be meaningfully interpreted.
  • No Scaling Required: It doesn’t require input features to be scaled or standardized (you can also tranform for efficient computation).
  • Works Well with Linearly Separable Data: Performs well when the data is linearly separable.

Cons

  • Assumes Linearity: Assumes a linear relationship between the independent variables and the log-odds of the dependent variable.
  • Sensitivity to Outliers: Outliers can affect the model’s performance and accuracy.
  • Overfitting: Can overfit if the dataset has a large number of features compared to the number of observations.
  • Limited to Binary Outcomes: Standard logistic regression is designed for binary classification and may not perform as well with multiclass classification problems.
  • Assumes Independence of Errors: Assumes that the observations are independent of each other and that there is no multicollinearity among predictors.

🥳 It’s party time 🥂