Code
| country | continent | lifeExp | pop | gdpPercap |
|---|---|---|---|---|
| Afghanistan | Asia | 43.828000 | 31889923 | 974.580338 |
| Albania | Europe | 76.423000 | 3600523 | 5937.029526 |
| Algeria | Africa | 72.301000 | 33333216 | 6223.367465 |
| Angola | Africa | 42.731000 | 12420476 | 4797.231267 |
Univariate distribution
Bivariate distribution
Multiple information
Time series data
Telling a story & Making a point
Gapminder dataset: world’s changes from \(1952\) to \(2007\).Video: Hans Rosling’s 200 Countries, 200 Years, 4 Minutes.| country | continent | lifeExp | pop | gdpPercap |
|---|---|---|---|---|
| Afghanistan | Asia | 43.828000 | 31889923 | 974.580338 |
| Albania | Europe | 76.423000 | 3600523 | 5937.029526 |
| Algeria | Africa | 72.301000 | 33333216 | 6223.367465 |
| Angola | Africa | 42.731000 | 12420476 | 4797.231267 |
Gapminder dataset: world’s changes from \(1952\) to \(2007\).Video: Hans Rosling’s 200 Countries, 200 Years, 4 Minutes.| pop | lifeExp | gdpPercap | |
|---|---|---|---|
| mean | 4.402122e+07 | 67.007423 | 11680.071820 |
| std | 1.476214e+08 | 12.073021 | 12859.937337 |
| min | 1.995790e+05 | 39.613000 | 277.551859 |
| 50% | 1.051753e+07 | 71.935500 | 6124.371108 |
| max | 1.318683e+09 | 82.603000 | 49357.190170 |
Gapminder dataset: world’s changes from \(1952\) to \(2007\).Video: Hans Rosling’s 200 Countries, 200 Years, 4 Minutes.from plotly.subplots import make_subplots
import plotly.graph_objects as go
fig = make_subplots(rows=1, cols=3,
subplot_titles=("Boxplot of pop", "Violinplot of lifeExp", "Histogram of GDP Per Capita"))
fig.add_trace(go.Box(y=data2007['pop'], name="pop"), col=1, row=1)
fig.add_trace(go.Violin(y=data2007['lifeExp'], name="lifeExp"), row=1, col=2)
fig.add_trace(go.Histogram(y=data2007['gdpPercap'],
name="gdpPercap"), row=1, col=3)
fig.update_layout(height=300, width=1000)
fig.update_yaxes(type="log", row=1, col=1)
fig.update_xaxes(title="Population", row=1, col=1)
fig.update_xaxes(title="Life Expectancy", row=1, col=2)
fig.update_xaxes(title="GDP Per Capita", row=1, col=3)
fig.show()Note
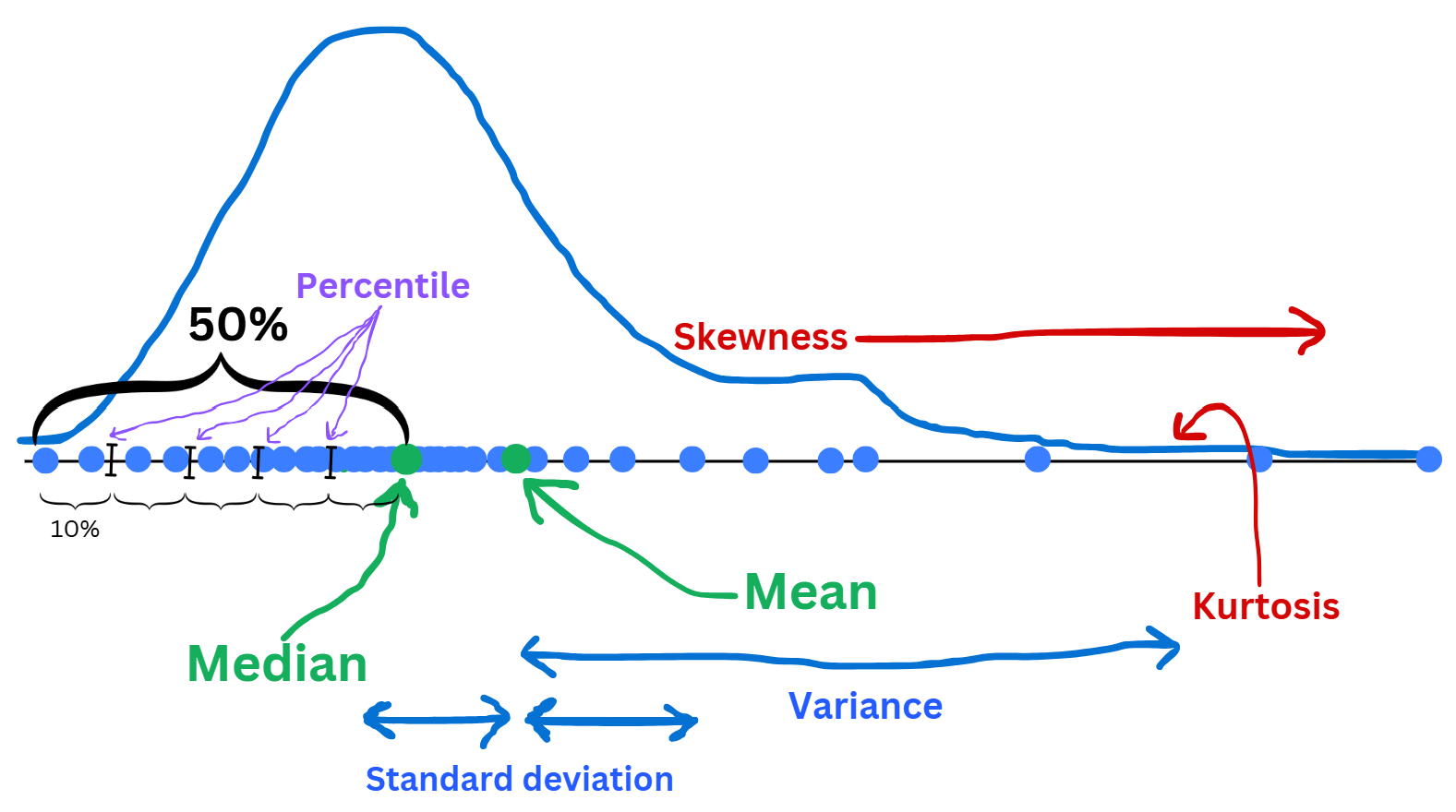
Note
Note
Gaussian kernel: \(K(t)=\frac{1}{\sqrt{2\pi}}e^{-t^2/2}\), then for any \(x\in\mathbb{R}\): \[\hat{f}(x)=\frac{1}{nh}\sum_{i=1}^nK\Big(\frac{x-x_i}{h}\Big).\]Note
Normal.Note
KDE + boxplot.KDE.Boxplot.Note
🤔 Anything interesting from these 3 correlation matrices?

"log" scaling!Are quantitative data on each category of the qualitative data different?
Different = Influenced = Related.
Just use what we have learned:
sorted_data = data2007.sort_values(by='lifeExp')
fig = px.box(data2007, x="continent", y="lifeExp", hover_name="country", color="continent", category_orders={'continent': sorted_data['continent']})
fig.update_layout(title="Life Expectancy on each continent in 2007", height=350, width=450)
fig.show()We grouped gdpPercap into 3 classes:
Are the categories of the 1st qualitative data different on each category of the 2nd qualitative variable?
Mosaic plot represents this effect.
Different = Influenced = Related.
from statsmodels.graphics.mosaicplot import mosaic
import pandas as pd
fig, ax = plt.subplots(figsize=(9, 5))
def prop(key):
if "Asia" in key:
return {'color': '#51cb4b'}
if "Europe" in key:
return {'color': '#dda63e'}
if "Africa" in key:
return {'color': '#e35441'}
if "Americas" in key:
return {'color': '#41b4e3'}
if "Oceania" in key:
return {'color': '#b374df'}
data2007['gdp_category'] = pd.qcut(data2007['gdpPercap'], q=3, labels=['Developing', 'Emerging', 'Developed'])
mosaic(data2007, ['continent','gdp_category'], gap=0.01, properties = prop, label_rotation=30, ax=ax)
plt.show()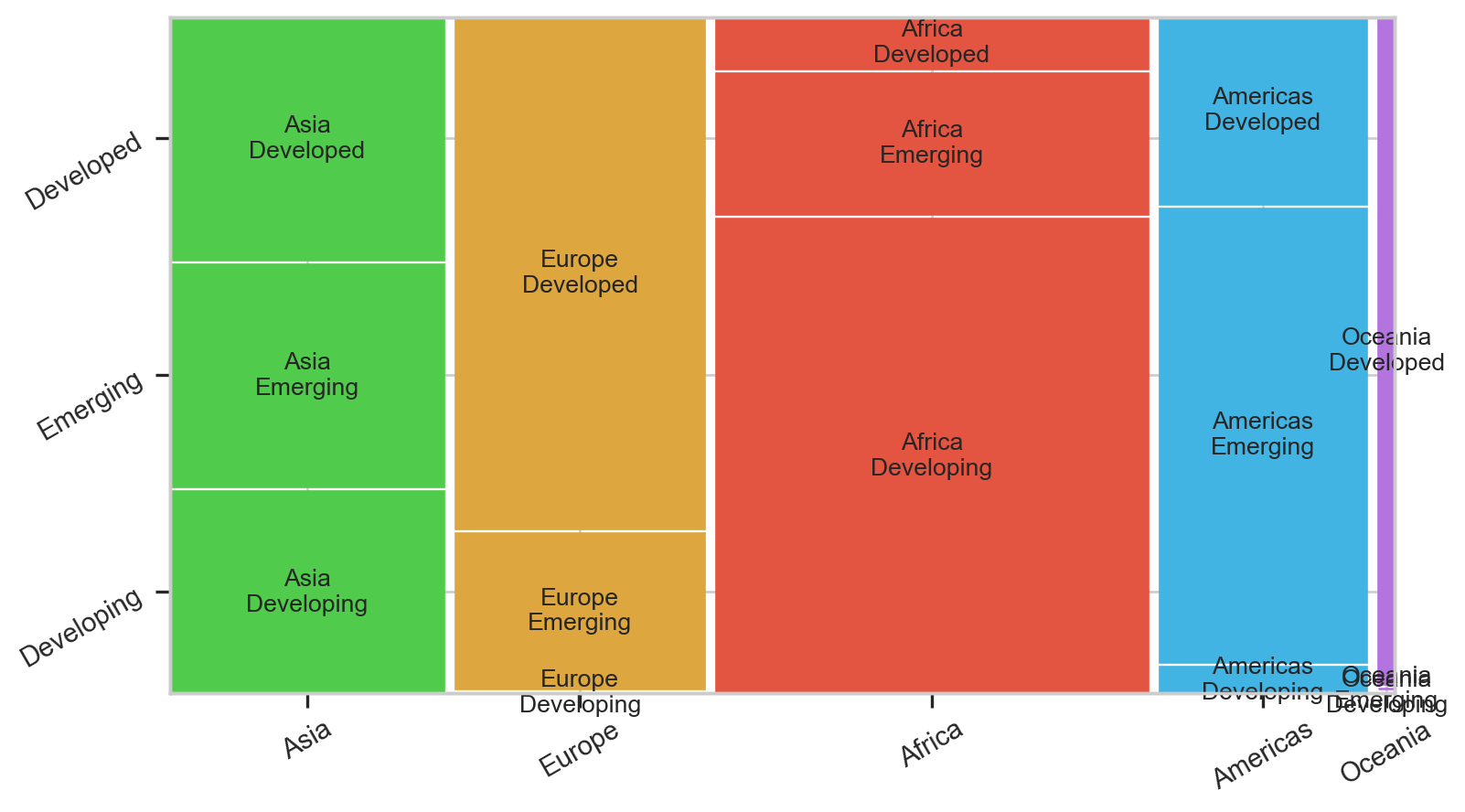
Grouped barplot is an alternative graph representing connection between two qualitative variables.
Different = Influenced = Related.
Color: can represent both quantitative (in form of gradient) and qualitative data (discrete color).
Shape: can represent qualitative variables.
Size: can represent quantitative variables.
3D Graph: often used to represent relationship of 3 quantitative variables.
Cambodia from 1952 to 2007.
