Hypothesis Testing
z-test & t-test
Outline
Motivation Example
Probability Review
z-Test
t-test
Examples
Hypothesis Testing
Is all about using
Normal behavior to reject
What’s not so normal!
Motivation Example
Motivation Example
Newborn baby weights
The weight of new born babies is an important
indicator for the baby’s health.Assumption: Newborn babies who weigh more
than the average weight of newborns are considered healthy.
Tell me, what should I do to check if my newborn brother is healthy?

Motivation Example
Newborn baby weights
- We should first estimate the average weight of newborn babies.
- A collected sample of size \(n=100\) gives \(\overline{W}=3.5\) kg.
- We don’t know the true healthy weight. Can we trust this estimate?
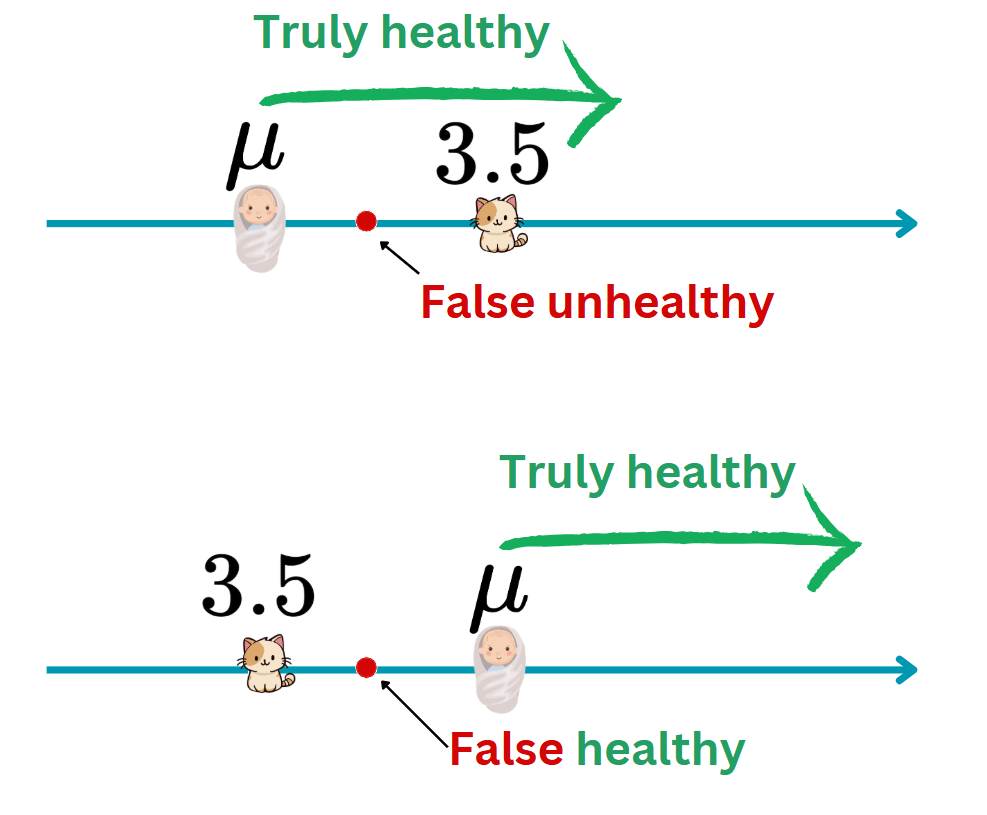
- If \(\mu\) is the true mean of baby weight, there’re 2 problems:
- If \(\mu < 3.5\), healthy babies may be considered unhealthy.
- If \(\mu > 3.5\), unhealthy babies may be considered healthy.
- One of these two mistakes is much much more important than another! Which one? Call it Type I Mistake, and we must control it!
:::
Motivation Example
Hypothesis setting and goal
- In this case, we want to build a decision rule that
- Judges babies based on the estimate \(\overline{W}=3.5\) and
- Controls the risk of committing Type I Mistake to be small.
- Here is the corresponding hypothesis test: \[\begin{cases}\color{red}{H_0}:\mu\geq 3.5\\ \color{green}{H_1}: \mu<3.5,\end{cases}\] where
- \(\color{red}{H_0}:\) Null hypothesis to be rejected with low risk of comitting Type I Mistake.
- \(\color{green}{H_1}:\) Alternative hypothesis to be supported.

Motivation Example
Hypothesis setting and goal (summary)
In this chapter, we aim to test simple hypothesis testing of the form: \[\begin{cases}\color{red}{H_0}:\mu=\color{blue}{\mu_0}\\{ }\\ \color{green}{H_1}: \mu\underset{<}{\overset{>}{\neq}} \color{blue}{\mu_0},\end{cases}\]
For any significance level \(\color{red}{\alpha}\in(0,1)\), often be \(0.05\), we aim to design a rule to reject \(\color{red}{H_0}\) under \(\color{red}{\text{Type I Error}}=\mathbb{P}(\color{red}{\text{Reject }H_0}|H_0\text{ is True})\leq \color{red}{\alpha}\).
To this goal, we need some tools from Probability!
Practice: I would open a ☕ coffee shop at a location if the sell count is at least \(500\) cups per day. Write the null and alternative hypotheses.
Probability Review
Probability
Sample space & Events
- Sample space: The set of all the outcomes of a random experiment.
- Events: Subsets of the sample space \(\Omega\).
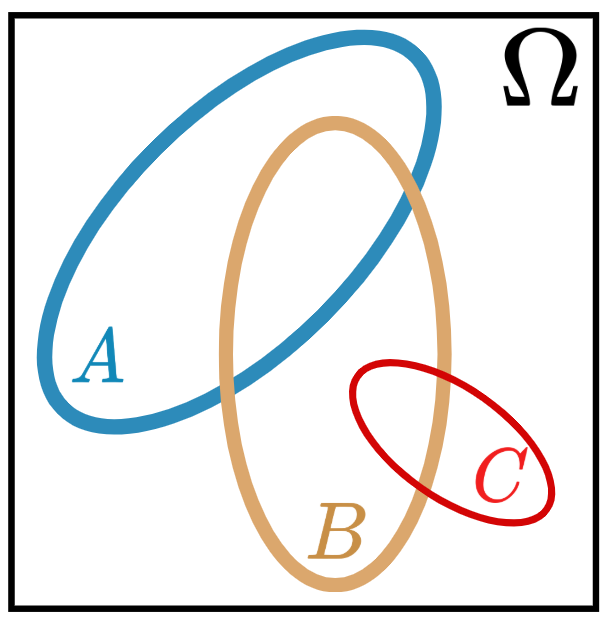
- Example: If I toss a coin (H and T) three times, then
- Sample space: \(\Omega=\{\) HHH, HHT, HTH, THH, HTT, THT, TTH, TTT \(\}\).
- Events:
- A: “Head came out twice”?
- B: “No head before tails”?
- C: “Number of heads and tails are equal”?
Probability
Sample space & Events
- Sample space: The set of all the outcomes of a random experiment.
- Events: Subsets of the sample space \(\Omega\).
- Example: If I toss a coin (H and T) three times, then
- Sample space: \(\Omega=\{\) HHH, HHT, HTH, THH, HTT, THT, TTH, TTT \(\}\).
- Events:
- A: “Head came out twice”, {HHT, HTH, THH}.
- B: “No head before tails”, {THH, TTH, TTT}.
- C: “Number of heads and tails are equal”, { } = ∅.
Probability
Probability on a fintie set
- Probabilty on a finite set: if \(A\subset \Omega\) then \(\color{blue}{\mathbb{P}(A)=\frac{n(A)}{n(\Omega)}}.\)
- Previous example: Coin toss (H and T) 3 times:
- Sample space: \(n(\Omega)=8\).
- Probability:
- A: “Head came out twice”, \(\mathbb{P}(A)=3/8\).
- B: “No head before tails”, \(\mathbb{P}(B)=3/8\).
- C: “Number of heads and tails are equal”, \(\mathbb{P}(C)=0\).
Probability
Axioms of probability
- Probability satisfies the following 3 axioms:
- \(\mathbb{P}(A)\geq 0\) for all \(A\subset \Omega\).
- \(\mathbb{P}(\Omega)=1\).
- If \(A,B\subset\Omega\) are two disjoint events, then \[\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B).\]
- Theorem: \(\color{blue}{A,B\subset\Omega: \mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)}.\)
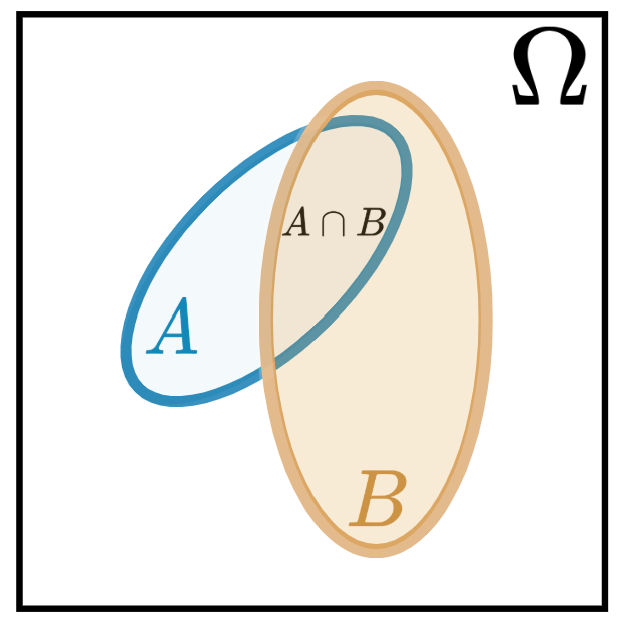
- Our example: \(\mathbb{P}(A\cup B)=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)=3/8+3/8-1/8=5/8\).
Probability
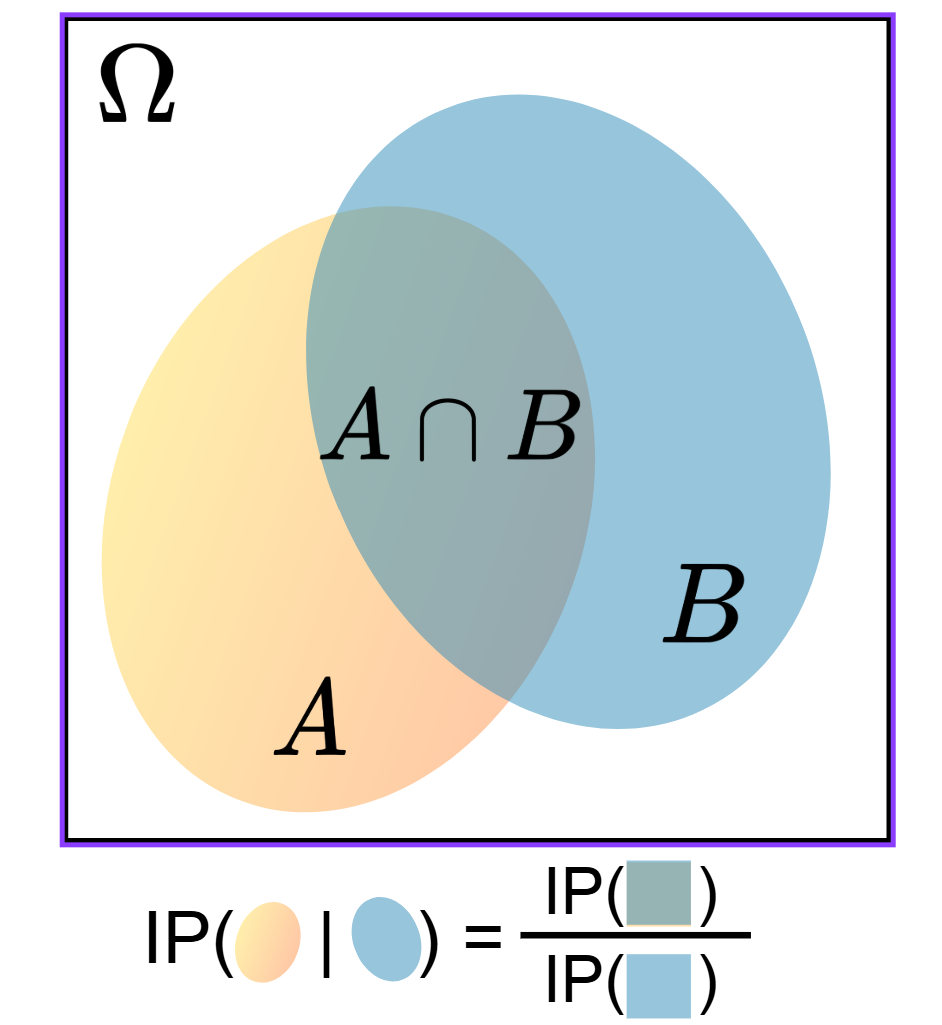
Conditional Probability & Independency
- If \(A,B\subset \Omega:\) with \(\mathbb{P}(B)>0\), the conditional probability of \(A\) given \(B\) is defined by: \[\color{blue}{\mathbb{P}(A|B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}=\frac{n(A\cap B)}{n(B)}}.\]
- Example: \(\mathbb{P}(A|B)=\frac{1/8}{3/8}=1/3\).
- An event \(A\) is independent of \(B\), denoted by \(A\perp B\) if and only if: \[\color{blue}{\mathbb{P}(A|B)=\mathbb{P}(A)}.\]
Probability
Discrete Random Variable
- Any function that maps outcomes to real numbers are called Random Variables (RV), often denoted by \(X,Y,Z,...\)
- If \(X\) takes only discrete values (for example, in {0,1,2,3,…}), it’s called a Discrete RV.
- In coin toss example, if \(X=\) number of heads, then \(X\in\{0,1,2,3\}\):
| \(\omega\) | \(X\) |
|---|---|
| TTT | \(0\) |
| HTT, THT, TTH | \(1\) |
| HHT, HTH, HHT | \(2\) |
| HHH | \(3\) |
- Compute probability for DRV: \[p_k=\mathbb{P}(X=k)=\mathbb{P}(\{\omega:X(\omega)=k\}).\]
- Our example: \(\mathbb{P}(X=0)=1/8.\)
- \(\mathbb{P}(X=1)=\mathbb{P}(X=2)=3/8.\)
- \(\mathbb{P}(X=3)=1/8.\)
Probability
Discrete Random Variable
- Any function that maps outcomes to real numbers are called Random Variables (RV), often denoted by \(X,Y,Z,...\)
- If \(X\) takes only discrete values (for example, in {0,1,2,3,…}), it’s called a Discrete RV.
- In coin toss example, if \(X=\) number of heads, then \(X\in\{0,1,2,3\}\):
| \(\omega\) | \(X\) | \(p_k\) |
|---|---|---|
| TTT | \(0\) | \(1/8\) |
| HTT, THT, TTH | \(1\) | \(3/8\) |
| HHT, HTH, HHT | \(2\) | \(3/8\) |
| HHH | \(3\) | \(1/8\) |
- Compute probability for DRV: \[p_k=\mathbb{P}(X=k)=\mathbb{P}(\{\omega:X(\omega)=k\}).\]
- Our example: \(\mathbb{P}(X=0)=1/8.\)
- \(\mathbb{P}(X=1)=\mathbb{P}(X=2)=3/8.\)
- \(\mathbb{P}(X=3)=1/8.\)
Probability
Graph: barplot
| \(\omega\) | \(X\) | \(p_k\) |
|---|---|---|
| TTT | \(0\) | \(1/8\) |
| HTT, THT, TTH | \(1\) | \(3/8\) |
| HHT, HTH, HHT | \(2\) | \(3/8\) |
| HHH | \(3\) | \(1/8\) |
- 🔑 Remark: Qualitative data are often modeled using discrete random variables.
- Ex: Gender, Time of day, Traffic Level,…
Probability
Expectation & variance of DRV
- If \(X\) is a discrete random variable taking values in \(\{x_1,x_2,\dots,x_n\}\)
- The Expectation of \(X\): \[\mu=\mathbb{E}(X)=\sum_{k=1}^{n}x_kp_k.\]
- The Variance of \(X\): \[\sigma^2=\mathbb{V}(x)=\sum_{k=1}^np_k(x_k-\mu)^2.\]
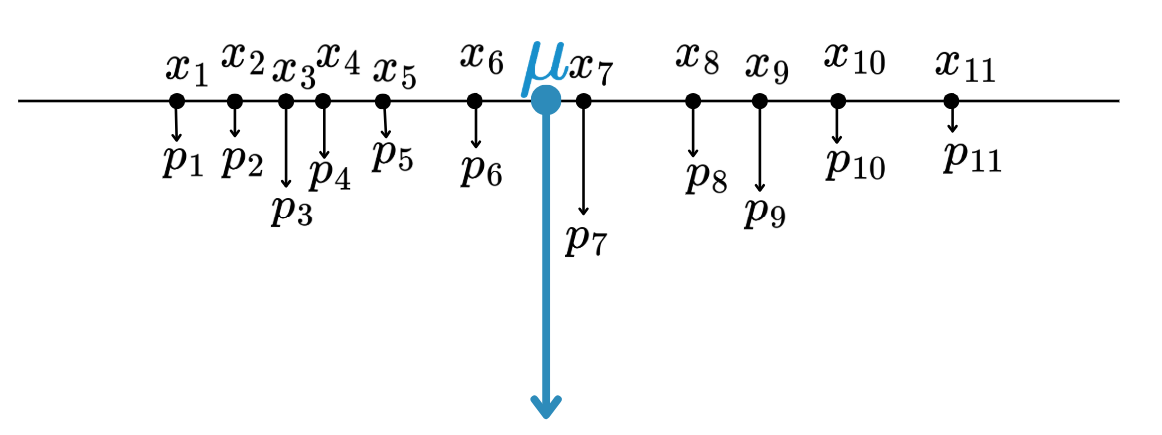
- Our example: \(X\) = Number of heads: \[\begin{align*}\mathbb{E}(X)&=\sum_{k=1}^{n}x_kp_k\\ &=0(1/8)+1(3/8)+2(3/8)+3(1/8)=1.5\\ \mathbb{V}(X)&=\sum_{k=1}^{n}p_k(x_n-1.5)^2\\ &=(0-1.5)^2(1/8)+(1-1.5)^2(3/8)+(2-1.5)^2(3/8)\\ &+(3-1.5)^2(1/8)=0.75.\end{align*}\]
Probability
Some well-known DRV: Bernoulli RV
- For modeling a coin toss or any experiments with only two outcomes: sucess (1) or failure (0), happening with probability \(\color{green}{p}\) and \(\color{red}{1-p}\) respectively.
- A Bernoulli RV \(X\) of parameter \(p\) is denoted by \(X\sim{\cal B}(p)\), and has the following Probability Mass Function (PMF):
| \(X=k\) | \(p_k=\mathbb{P}(X=k)\) |
|---|---|
| \(\color{green}{1}\) | \(\color{green}{p}\) |
| \(\color{red}{0}\) | \(\color{red}{1-p}\) |
- Q2: Check that if \(X\) is a Bernoulli RV of success probability \(p\) denoted by \(X\sim{\cal B}(p)\), then:
- \(\mathbb{E}(X)=p\)
- \(\mathbb{V}(X)=p(1-p).\)
- Ex: Data that can be modeled using Bernoulli RV:
- Gender: Male (1), female (0)
- Disease: Positive (1), negative (0)…
Probability
Some well-known DRV: Binomial RV
- For modeling the number of sucesses that occured in \(\color{red}{n}\) times of independent Bernoulli experiments of some parameter \(p\).
- If \(X\) is a Binomial RV denoted by \(X\sim{\cal Bin}(n,p)\) then:
- It takes values \(k\in\{0,1,...,n\}\) with
- PMF: \(p_k=\mathbb{P}(X=k)=C(n,k)p^k(1-p)^{n-k}=\binom{n}{k}p^k(1-p)^{n-k},\) with
- \(n!=n\times(n-1)\times\dots \times 1\), called “\(n\) factorial”, and
- \(C(n,k)=\binom{n}{k}=\frac{n!}{(n-k)!k!}\) the number of ways to choose \(k\) objects at once (no order) from \(n\) objects.
| \(X\) | \(0\) | \(1\) | \(2\) | \(\dots\) | \(n\) |
|---|---|---|---|---|---|
| \(p_k\) | \((1-p)^n\) | \(np(1-p)^{n-1}\) | \(\frac{n(n-1)}{2}p^2(1-p)^{n-2}\) | \(\dots\) | \(p^n\) |
Probability
Barplot of binomial distribution
- Table of distribution:
| X | \(0\) | \(1\) | \(2\) | \(\dots\) | \(n\) |
|---|---|---|---|---|---|
| \(p_k\) | \((1-p)^n\) | \(np(1-p)^{n-1}\) | \(\frac{n(n-1)}{2}p^2(1-p)^{n-2}\) | \(\dots\) | \(p^n\) |
- Q3: Check that if \(X\sim{\cal Bin}(n,p)\), then:
- \(\mathbb{E}(x)=np\)
- \(\mathbb{V}(x)=np(1-p).\)
- Ex: If the prob. of mistakenly transferring money in “$” instead of “៛” in each transaction is \(0.01\), what’s the probability of making \(5\) mistakes in 100 transactions?
Probability
Some well-known DRV: Poisson
- For modeling the number of rare events such as the number of lost luggages at an airport.
- It requires a key parameter \(\lambda\) which is called intensity parameter.
- If \(X\) is a Poisson RV of parameter \(\lambda>0\) denoted by \(X\sim{\cal P}(\lambda)\) if and only if for each \(k=0,1,2,...\), \[p_k=\mathbb{P}(X=k)=e^{-\lambda}\frac{\lambda^{k}}{k!}\quad (e\approx 2.7182...)\]
- We have the table of its distribution:
| X | \(0\) | \(1\) | \(2\) | \(3\) | \(\dots\) |
|---|---|---|---|---|---|
| \(p_k\) | \(e^{-\lambda}\) | \(e^{-\lambda}\lambda\) | \(e^{-\lambda}\frac{\lambda^2}{2!}\) | \(e^{-\lambda}\frac{\lambda^3}{3!}\) | \(\dots\) |
Probability
Barplot of Poisson distribution
| X | \(0\) | \(1\) | \(2\) | \(3\) | \(\dots\) |
|---|---|---|---|---|---|
| \(p_k\) | \(e^{-\lambda}\) | \(e^{-\lambda}\lambda\) | \(e^{-\lambda}\frac{\lambda^2}{2!}\) | \(e^{-\lambda}\frac{\lambda^3}{3!}\) | \(\dots\) |
- Q4: Check that if \(X\sim{\cal P}(\lambda)\), then:
- \(\mathbb{E}(x)=\lambda\)
- \(\mathbb{V}(x)=\lambda.\)
- Poisson variable can be used to model:
- Number of eggs at a given farm/day
- Number of cars sold/day
- Number of mistakes in transections/day…
Probability
Continuous Random Variables
- A RV \(X\) that takes continuous values are called Continuous RV (CRV).
- Ex: Many things can be modeled using CRV:
- Newborn baby weights 👶
- Height of freshmen at AUPP 🫡
- Time that the latest student arrives to my DA I class 😏…
- How would we describe probability of \(\color{red}{X=x\in\mathbb{R}}\)?
- Probability Mass Function (PMF) \[p_k=\mathbb{P}(X=k),k=0,1,...\]
- It describes the probability that \(X\) takes value \(k\).
- Probability Density Function (PDF) \[f_X(x)=\text{A function of variable }x\]
- Roughly, it describes likelihood of \(X\) taking values around \(x\in\mathbb{R}\).
Probability
Continuous Random Variables
- A RV \(X\) that takes continuous values are called Continuous RV (CRV).
- Ex: Many things can be modeled using CRV:
- Newborn baby weights 👶
- Height of freshmen at AUPP 🫡
- Time that the latest student arrives to my DA I class 😏…
- How would we describe probability of \(\color{red}{X=x\in\mathbb{R}}\)?
- Probability Mass Function (PMF)
- Probability Density Function (PDF)
Probability
Properties of PDF
- If \(f_X\) is the PDF of a CRV \(X\) taking values in \(S\subset\mathbb{R}\), then it satisfies:
- Positivity: \(f_X(x)\geq 0\) for all \(x\in S\)
- Total Area Under the Curve is 1: \(\int_{S}f_X(x)dx=1\).
- Ex: Check that \(f(x)=x^2\) is a density of a RV defined on \(S=[0,\sqrt[3]{3}]\).
- We have \(f(x)=x^2>0\) for all \(x\in [0,\sqrt[3]{3}]\).
- Check total area under the curve: \[\begin{align*} \int_{S}f(x)dx&=\int_{0}^{\sqrt[3]{3}}x^2dx\\ &=\frac{1}{3}\left[x^3\right]_0^{\sqrt[3]{3}}\\ &= ((\sqrt[3]{3})^3-0^3)/3=1. \end{align*}\]
Probability
Compute Probability with PDF
- Formula: if \(f_X\) is the density of a random variable \(X\) taking values in \(S\subset\mathbb{R}\), thus for any \(a,b\in S\) with \(a<b\), one has
\[\color{red}{\mathbb{P}(a<X<b)=\mathbb{P}(a\leq X<b)=\mathbb{P}(a<X\leq b)=\mathbb{P}(a\leq X\leq b)=\int_{a}^bf_X(x)dx.}\]
- Remark: If \(X\) is a CRV, then \(\color{red}{\mathbb{P}(X=a)=0}\) for all \(a\in S\).
- Ex: If \(X\) is a RV with PDF \(f(x)=x^2\), taking values in \(S=[0,\sqrt[3]{3}]\). Compute:
- \(\mathbb{P}(0\leq X<\sqrt[3]{3}/2)\)
- \(\mathbb{P}(\sqrt[3]{3}/2\leq X\leq \sqrt[3]{3})\)
Probability
Expectation and variance of CRV
- If \(X\) is a CRV with PDF \(f_X\) then
- Expectation: \(\mu=\mathbb{E}(X)=\int_{S}xf_X(x)dx.\)
- Variance: \[\sigma^2=\mathbb{V}(X)=\mathbb{E}[(X-\mu)^2]=\int_{S}(x-\mu)^2f_X(x)dx.\]
- Example: Check that if \(X\) is a CRV with PDF \(f_X(x)=x^2\) defined on \(S=[0,\sqrt[3]{3}]\), one has
- \(\mathbb{E}(X)=\int_0^{\sqrt[3]{3}}xf_X(x)dx=\frac{3\sqrt[3]{3}}{4}.\)
- \(\mathbb{V}(X)=\frac{3^{5/3}}{5}-\frac{3^{8/3}}{16}.\)
Probability
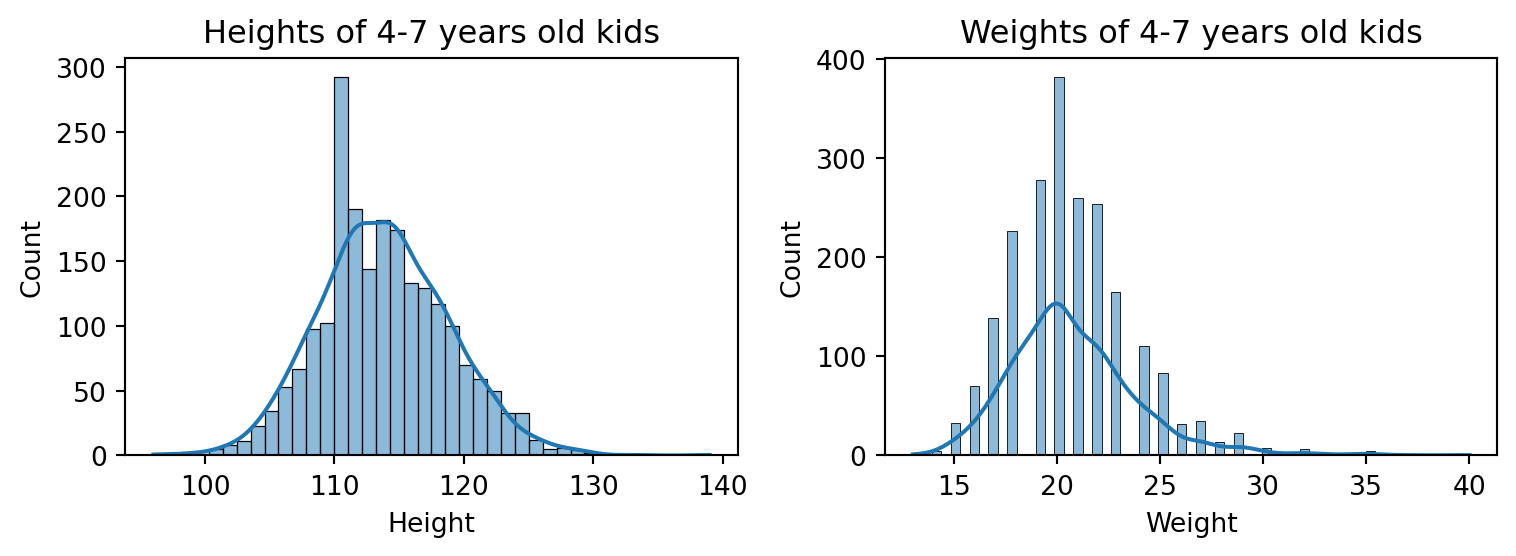
Normal/Gaussian Random Variable
- For modeling natural measurements such as
- Heights, weights, sizes…
- Measurement errors…
- A RV normal or Gaussian with mean \(\mu\) and variance \(\sigma^2\) is denoted by \(X\sim {\cal N}(\color{green}{\mu}, \color{red}{\sigma^2})\).
- Its PDF is defined for all \(x\in\mathbb{R}\) by \[f_X(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-\color{green}{\mu})^2/(2\color{red}{\sigma^2})}.\]
- We can check that
- \(\mathbb{E}(X)=\color{green}{\mu}\) and \(\mathbb{V}(X)=\color{red}{\sigma^2}.\)
Probability
Normal/Gaussian Random Variable
- Consider our French kid dataset:
| Gender | Age | Height | Weight | |
|---|---|---|---|---|
| 1 | M | 74 | 116 | 18 |
| 2 | M | 69 | 120 | 23 |
| 3 | M | 72 | 121 | 25 |
Probability
Standard Normal & Property
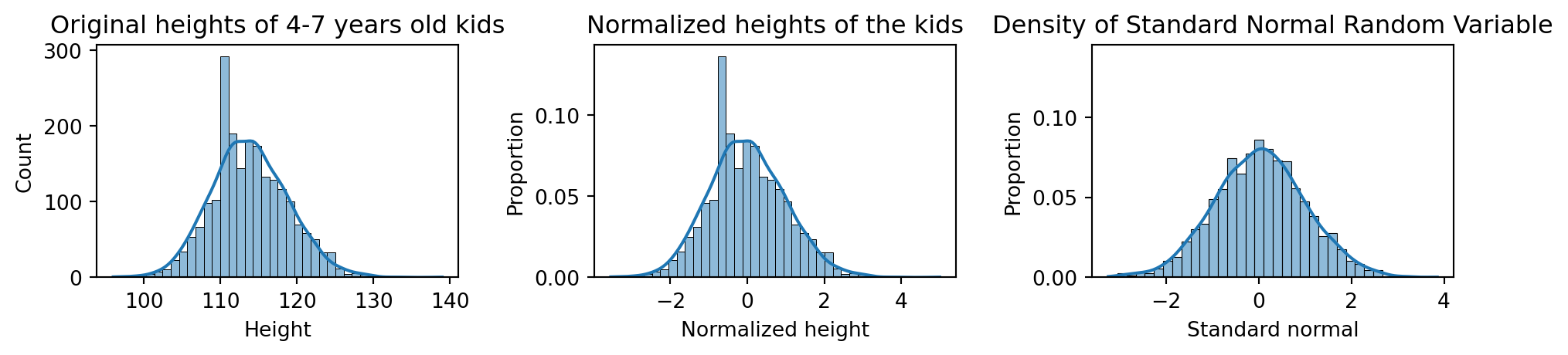
Standard Normal & The main property
A normal RV with mean \(\mu=0\) and variance \(\sigma^2=1\), denoted by \(X\sim{\cal N}(0,1)\), is called “Standard Normal Random Variable”.
If \(X_1,\dots, X_n\sim{\cal N}(\color{green}{\mu},\color{red}{\sigma^2})\) are Independent and Identically Distributed (iid) and \(\overline{X}_n=\sum_{i=1}^nX_i/n\) then \[Z=\frac{\overline{X}_n-\color{green}{\mu}}{\color{red}{\sigma}/\sqrt{n}}\sim {\cal N}(0,1).\]
Probability
Standard Normal & Property
Standard Normal & The main property
A normal RV with mean \(\mu=0\) and variance \(\sigma^2=1\), denoted by \(X\sim{\cal N}(0,1)\), is called “Standard Normal Random Variable”.
If \(X_1,\dots, X_n\sim{\cal N}(\color{green}{\mu},\color{red}{\sigma^2})\) are Independent and Identically Distributed (iid) and \(\overline{X}_n=\sum_{i=1}^nX_i/n\) then \[Z=\frac{\overline{X}_n-\color{green}{\mu}}{\color{red}{\sigma}/\sqrt{n}}\sim {\cal N}(0,1).\]
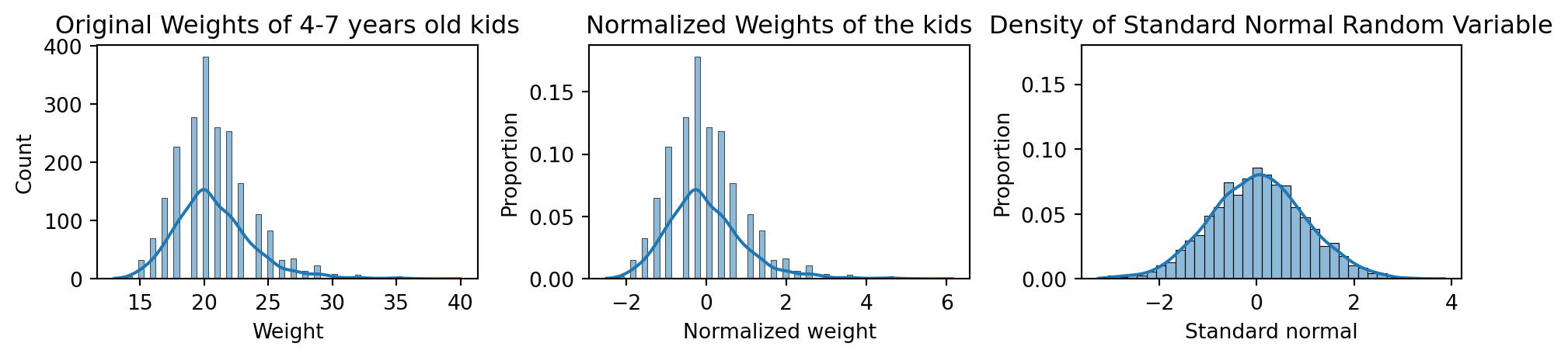
Probability
Standard Normal & Property
- If \(Z\sim{\cal N}(0,1)\), then we know its range very well!
Probability
Standard Normal & Property
- NO ONE CAN COMPUTE THE EXACT VALUE OF \(\mathbb{P}(a\leq Z\leq b)\) for all \(a<b\)!
- People use the following standard normal \(z\) table:
Probability
Challenge 👉 Demo
If \(Z\sim{\cal N}(0,1)\), use \(z\)-table to compute:
- \(\mathbb{P}(Z\leq 0)\)
- \(\mathbb{P}(Z\leq -1)\)
- \(\mathbb{P}(Z\leq 1.37)\)
- \(\mathbb{P}(Z\leq 2.15)\)
- \(\mathbb{P}(0.25< Z\leq 1.27)\)
- \(\mathbb{P}(-1.23 \leq Z < 0.14)\)
- \(\mathbb{P}(Z\geq 2.71)\)
- \(\mathbb{P}(Z>1.96)\)
- \(\mathbb{P}(Z<-0.7)\)
- \(\mathbb{P}(|Z|\geq 1.96)\)
- \(\mathbb{P}(|Z|> 2.5)\)
- \(\mathbb{P}(|Z|< 1.37)\)
- \(\mathbb{P}(|Z|\leq 2.15)\)
- Find \(z_0\) such that \(\mathbb{P}(Z< z_0)=0.9\)
- Find \(z_0\) such that \(\mathbb{P}(Z\geq z_0)=0.314\)
- Find \(z_0\) such that \(\mathbb{P}(|Z|\geq z_0)=0.05\)
- Find \(z_0\) such that \(\mathbb{P}(|Z|\leq z_0)=0.75\)
- Find \(z_0\) such that \(\mathbb{P}(|Z|\leq z_0)=0\).

And now, we have enough probability tools!
\(z\)-Test
z-Test
Recall
- Suppose a sample (weights): \(X_1,X_2,\dots, X_n\in\mathbb{R}\).
- For any \(\color{blue}{\mu_0}\in\mathbb{R}\) we would like to test the following hypothesis: \[(S_>):\begin{cases}H_0: \text{The true mean }\mu=\color{blue}{\mu_0}\\ H_1: \text{The true mean }\mu>\color{blue}{\mu_0}. \end{cases}\]
- In other words, we want to reject \(H_0\) with a small risk of committing Type I Error (= reject \(H_0\) while it’s true).
- This can be done by deploying two important ideas:
- The original data should be well behaved (Gaussian).
- Based on the data, build a quantity that we can guess its range.
z-Test
Z-statistics and Rejection Region
Z-test statistics & Rejection Region
- Key assumption: Assume that \(X_1,\dots,X_n\sim{\cal N}(\mu, \sigma^2)\) are iid with an unknown mean \(\mu\) and a known standard deviation \(\sigma>0\).
- If \(H_0\) is True, then for any \(\color{red}{\alpha}\in (0,1)\) we have
- The quantity: \(Z=\frac{\overline{X}_n-\color{blue}{\mu_0}}{\sigma/\sqrt{n}}\sim{\cal N}(0,1)\) “z-value”.
- If we choose \(\color{red}{z_{\alpha}}\) such that \(\mathbb{P}(Z>\color{red}{z_{\alpha}})=\color{red}{\alpha}\), then “if we reject \(H_0\) whenever \(Z>\color{red}{z_{\alpha}}\), it’s guaranteed that” \[\mathbb{P}(\color{red}{\text{Type I Error}})=\mathbb{P}(\color{red}{\text{Reject }}H_0|H_0\color{blue}{\text{ is True}})=\color{red}{\alpha}.\]
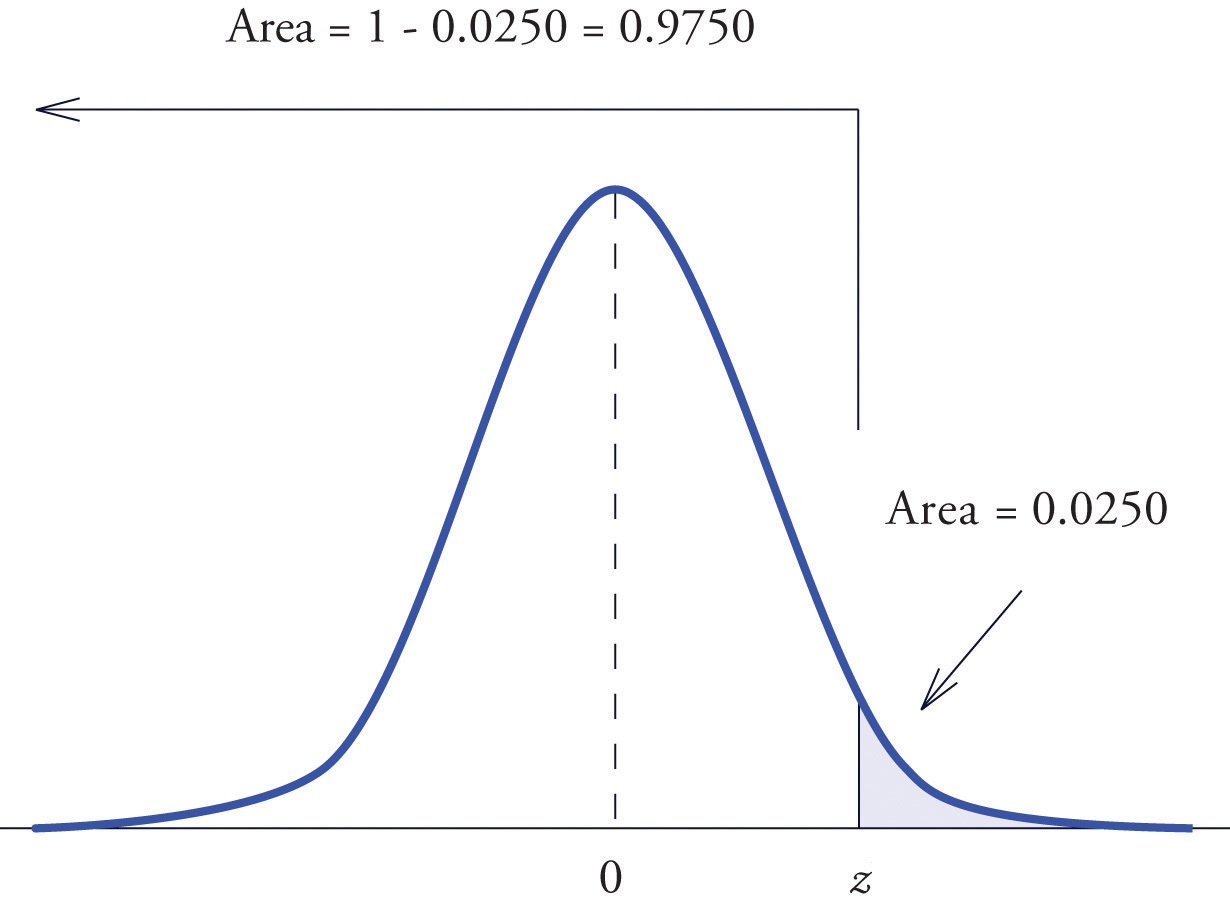
- The set of \(\color{red}{R(\alpha)=\{z: z>z_{\alpha}\}}\) is called Rejection Region at level \(\alpha\), meaning that if \(Z\in\color{red}{R(\alpha)}\), we can reject \(H_0\) with confidence level \(1-\color{red}{\alpha}\).
z-Test
Z-test Summary for (\(S_>\), one-tailed)
Z-test Summary (\(S_>\))
- Suppose the sample: \(X_1,\dots,X_n\sim{\cal N}(\mu,\sigma^2)\) with known \(\sigma^2\) and unknown \(\mu\).
- For some \(\color{blue}{\mu_0}\) given, to test \(H_0:\mu=\color{blue}{\mu_0}\) against \(H_1:\mu>\color{blue}{\mu_0}\) we do:
- Compute \(Z=\frac{\overline{X}_n-\color{blue}{\mu_0}}{\sigma/\sqrt{n}}\)
- For a given significance level \(\color{red}{\alpha}\), compute \(\color{red}{z_\alpha}\) such that \(\mathbb{P}(Z\geq\color{red}{z_\alpha})=\color{red}{\alpha}\).
- Decision:
- If \(Z\geq\color{red}{z_\alpha}\), we reject \(H_0\) with confidence level \(1-\color{red}{\alpha}\).
- If \(Z< \color{red}{z_\alpha}\), we CANNOT \(H_0\) due to insufficient evidence.

z-Test
Z-test Summary for (\(S_<\), one-tailed)
Z-test Summary (\(S_<\))
- Suppose the sample: \(X_1,\dots,X_n\sim{\cal N}(\mu,\sigma^2)\) with known \(\sigma^2\) and unknown \(\mu\).
- For some \(\color{blue}{\mu_0}\) given, to test \(H_0:\mu=\color{blue}{\mu_0}\) against \(H_1:\mu<\color{blue}{\mu_0}\) we do:
- Compute \(Z=\frac{\overline{X}_n-\color{blue}{\mu_0}}{\sigma/\sqrt{n}}\)
- For a given significance level \(\color{red}{\alpha}\), compute \(\color{red}{z_\alpha}\) such that \(\mathbb{P}(Z\leq\color{red}{z_\alpha})=\color{red}{\alpha}\).
- Decision:
- If \(Z\leq\color{red}{z_\alpha}\), we reject \(H_0\) with confidence level \(1-\color{red}{\alpha}\).
- If \(Z> \color{red}{z_\alpha}\), we CANNOT reject \(H_0\) due to insufficient evidence.
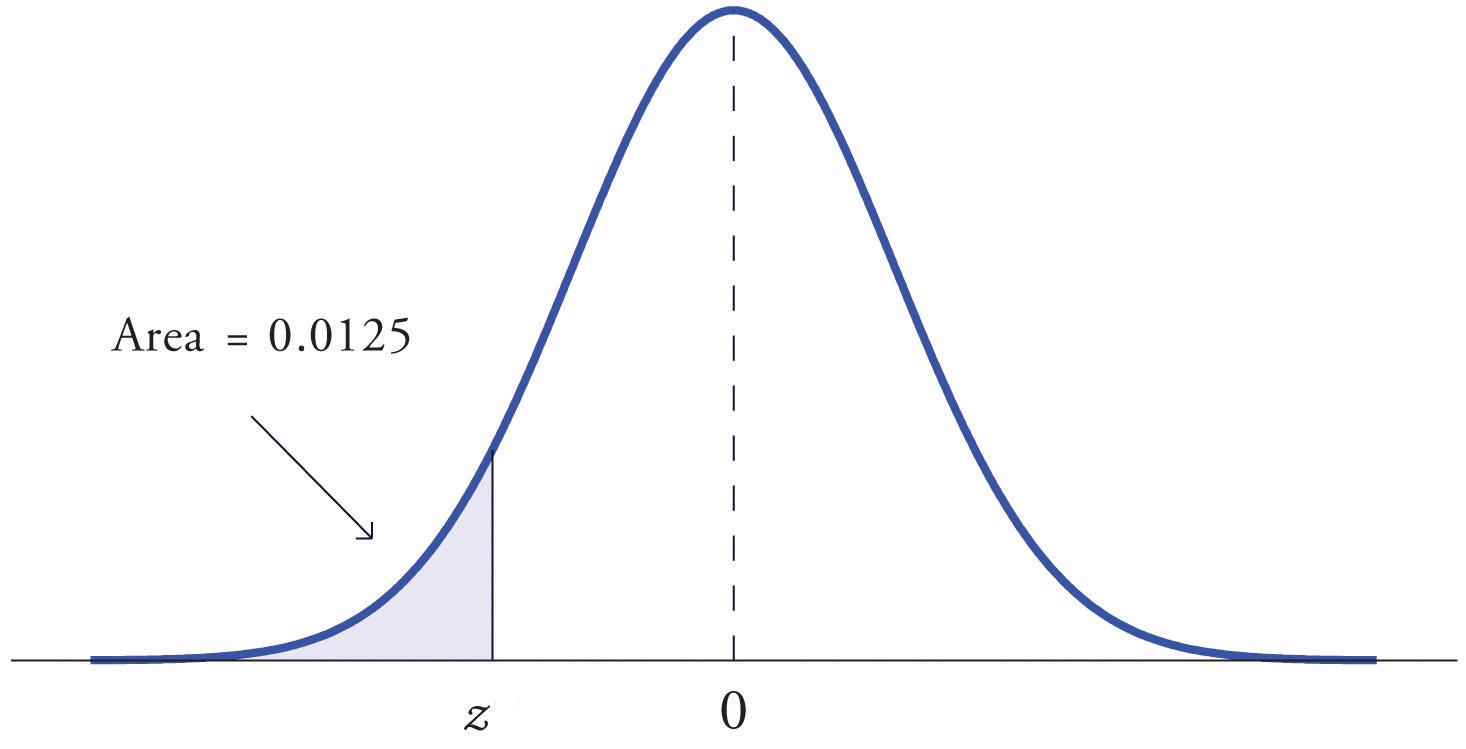
- Ex: (Baby weight) Test \(H_0:\mu=3.75\) against \(H_1:\mu<3.75\) at \(\alpha=0.05\), knowing that \(\sigma=0.5\) kg and \(\overline{W}=3.5\) kg (assuming that baby weights are normally distributed). How about when \(\overline{W}=2.9\) kg?
z-Test
Z-test Summary for (\(S_\neq\) Two-tailed)
Z-test Summary (\(S_\neq\), two-sided test)
- Suppose the sample: \(X_1,\dots,X_n\sim{\cal N}(\mu,\sigma^2)\) with known \(\sigma^2\) and unknown \(\mu\).
- For some \(\color{blue}{\mu_0}\) given, to test \(H_0:\mu=\color{blue}{\mu_0}\) against \(H_1:\mu\neq\color{blue}{\mu_0}\) we do:
- Compute \(Z=\frac{\overline{X}_n-\color{blue}{\mu_0}}{\sigma/\sqrt{n}}\)
- For a given significance level \(\color{red}{\alpha}\), compute \(\color{red}{z_{\alpha/2}}\) such that \(\mathbb{P}(|Z|\geq\color{red}{z_{\alpha/2}})=\color{red}{\alpha}\).
- Decision:
- If \(|Z|\geq\color{red}{z_{\alpha/2}}\), we reject \(H_0\) with confidence level \(1-\color{red}{\alpha}\).
- If \(|Z|< \color{red}{z_{\alpha/2}}\), we CANNOT reject \(H_0\) due to insufficient evidence.
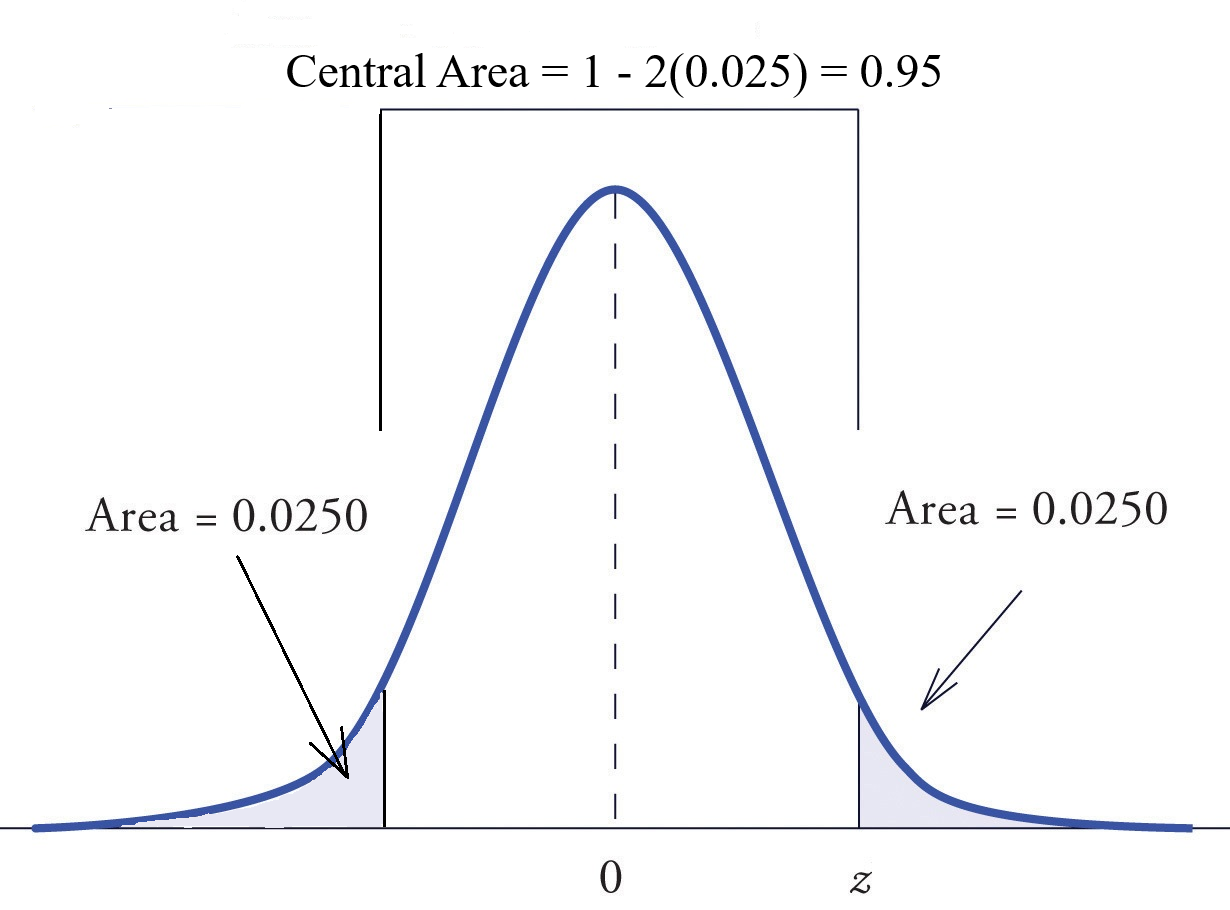
z-Test
Example: Newborn weights in France, 2016
- Test \(\color{red}{\mu=3}\) kg against \(\color{green}{\mu\neq 3}\) kg at significance level \(\alpha=0.1\), given that \(n=745000,\overline{X}_n=3.25\) and \(\sigma^2=1.5\). How about with \(\color{blue}{\mu_0=3.75}\)?
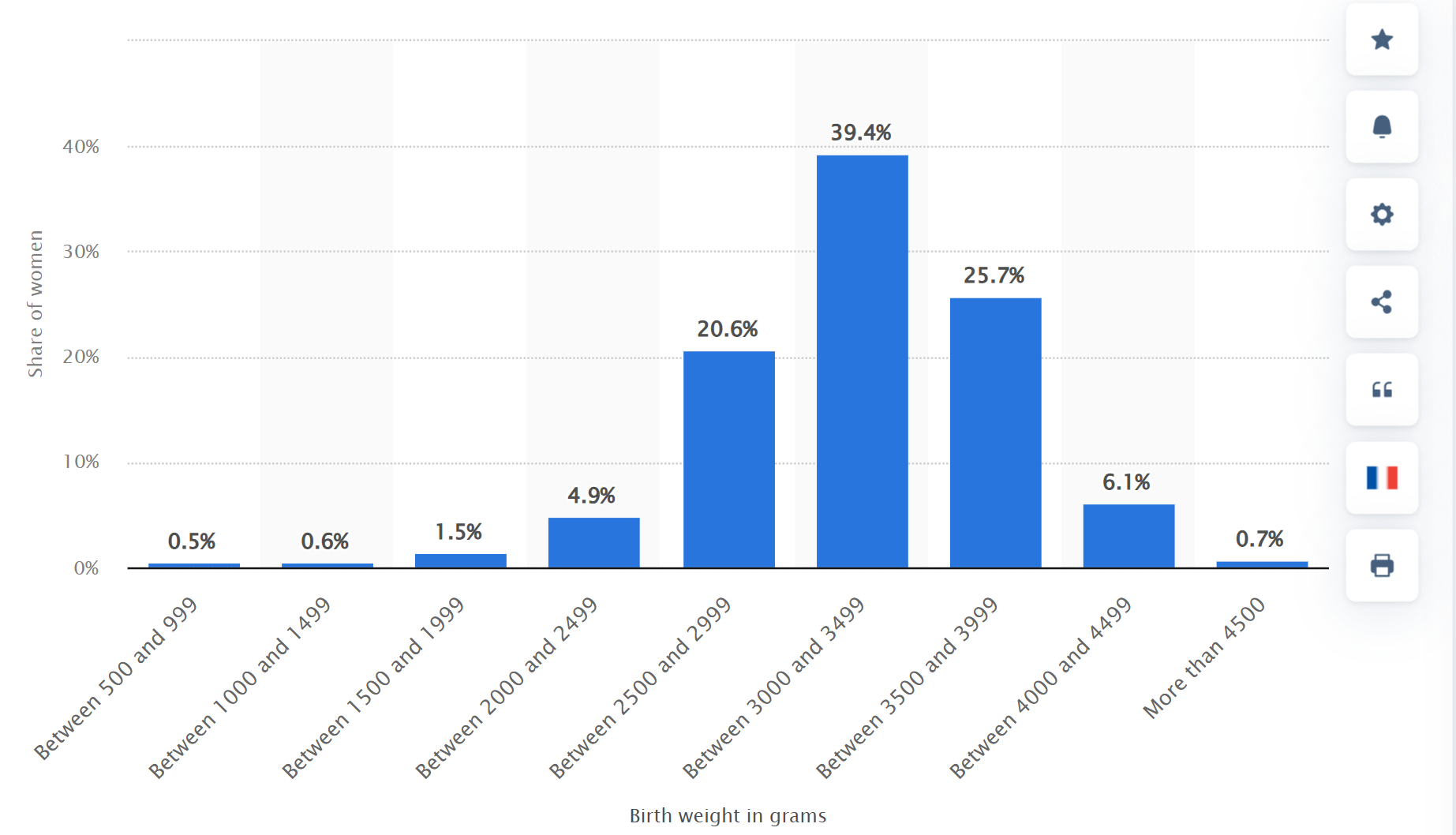
Source: Birth weight of newborns delivered in France 2016, Statistia.
\(t\)-Test
t-Test
\(t\)-distribution
- A Student or \(t\) RV is a CRV that behaves similarly to a Gaussian RV but with slightly heavier tails.
- A \(t\) RV \(T\) with degree of freedom (df) \(k\) is often denoted by \(T\sim{\cal T}(k)\).
- 🔑 As \(k\) increases, \({\cal T}(k)\to Z\sim{\cal N}(0,1)\).
t-Test
\(t\)-Table: tdistributiontable
- Just like Standard normal, we use \(t\)-table to find \(\mathbb{P}(\leq T(k))\).
t-Test
\(t\)-Test Challenge 👉 Demo
If \(T\sim{\cal T}(\text{df})\), use \(t\)-table to estimate:
- \(\mathbb{P}(T\leq 0)\) with df \(=15\).
- \(\mathbb{P}(T\leq -1)\) with df \(=10\).
- \(\mathbb{P}(T\leq 1.37)\) with df \(=15\).
- \(\mathbb{P}(T\leq 2.15)\) with df \(=13\).
- \(\mathbb{P}(0.25< T\leq 1.27)\) with df \(=30\).
- \(\mathbb{P}(-1.23 \leq T < 0.14)\) with df \(=21\).
- \(\mathbb{P}(T\geq 2.71)\) with df \(=10\).
- \(\mathbb{P}(T>1.96)\) with df \(=25\).
- \(\mathbb{P}(T<-0.7)\) with df \(=17\).
For the followings, df \(=23\):
- \(\mathbb{P}(|T|\geq 2.1)\)
- \(\mathbb{P}(|T|> 2.5)\)
- \(\mathbb{P}(|T|< 1.37)\)
- \(\mathbb{P}(|T|\leq 2.15)\)
- Find \(t_0\) such that \(\mathbb{P}(T< t_0)=0.9\)
- Find \(t_0\) such that \(\mathbb{P}(T\geq t_0)=0.35\)
- Find \(t_0\) such that \(\mathbb{P}(|T|\geq t_0)=0.05\)
- Find \(t_0\) such that \(\mathbb{P}(|T|\leq t_0)=0.75\)
- Find \(t_0\) such that \(\mathbb{P}(|T|\leq t_0)=0\).
t-Test
\(t\)-Table for (\(T_>\) one-tailed)
- When \(n\) is small (\(<30\)) and \(\sigma>0\) is unknown, we use \(t\)-distribution.
\(t\)-Test Summary (\(T_>\))
- Suppose the sample: \(X_1,\dots,X_n\sim{\cal N}(\mu,\color{red}{\sigma^2})\) with unknown \(\mu\) and \(\color{red}{\sigma^2}\).
- For some \(\color{blue}{\mu_0}\) given, to test \(H_0:\mu={\mu_0}\) against \(H_1:\mu>\color{blue}{\mu_0}\) we do:
- Compute \(\color{red}{\hat{\sigma}^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X}_n)^2}\) (estimator of \(\color{red}{\sigma^2}\)), then \(T=\frac{\overline{X}_n-\color{blue}{\mu_0}}{\color{red}{\hat{\sigma}}/\sqrt{n}}\)
- For a given significance level \(\color{red}{\alpha}\), compute \(\color{red}{t_\alpha}\) such that \(\mathbb{P}(T\geq\color{red}{t_\alpha})=\color{red}{\alpha}\).
- Decision:
- If \(T\geq\color{red}{t_\alpha}\), we reject \(H_0\) with confidence level \(1-\color{red}{\alpha}\).
- If \(T< \color{red}{t_\alpha}\), we CANNOT \(H_0\) due to insufficient evidence.

t-Test
\(t\)-Table for (\(T_<\) one-tailed)
\(t\)-Test Summary (\(T_<\))
- Suppose the sample: \(X_1,\dots,X_n\sim{\cal N}(\mu,\color{red}{\sigma^2})\) with unknown \(\mu\) and \(\color{red}{\sigma^2}\).
- For some \(\color{blue}{\mu_0}\) given, to test \(H_0:\mu={\mu_0}\) against \(H_1:\mu<\color{blue}{\mu_0}\) we do:
- Compute \(\color{red}{\hat{\sigma}^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X}_n)^2}\) (estimator of \(\color{red}{\sigma^2}\)), then \(T=\frac{\overline{X}_n-\color{blue}{\mu_0}}{\color{red}{\hat{\sigma}}/\sqrt{n}}\)
- For a given significance level \(\color{red}{\alpha}\), compute \(\color{red}{t_\alpha}\) such that \(\mathbb{P}(T\leq\color{red}{t_\alpha})=\color{red}{\alpha}\).
- Decision:
- If \(T\leq\color{red}{t_\alpha}\), we reject \(H_0\) with confidence level \(1-\color{red}{\alpha}\).
- If \(T> \color{red}{t_\alpha}\), we CANNOT \(H_0\) due to insufficient evidence.

t-Test
\(t\)-Table for (\(T_{\neq}\) two-tailed)
\(t\)-Test Summary (\(T_\neq\))
- Suppose the sample: \(X_1,\dots,X_n\sim{\cal N}(\mu,\color{red}{\sigma^2})\) with unknown \(\mu\) and \(\color{red}{\sigma^2}\).
- For some \(\color{blue}{\mu_0}\) given, to test \(H_0:\mu={\mu_0}\) against \(H_1:\mu\neq\color{blue}{\mu_0}\) we do:
- Compute \(\color{red}{\hat{\sigma}^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X}_n)^2}\) (estimator of \(\color{red}{\sigma^2}\)), then \(T=\frac{\overline{X}_n-\color{blue}{\mu_0}}{\color{red}{\hat{\sigma}}/\sqrt{n}}\).
- For a given significance level \(\color{red}{\alpha}\), compute \(\color{red}{t_\alpha}\) such that \(\mathbb{P}(|T|\geq\color{red}{t_\alpha})=\color{red}{\alpha}\).
- Decision:
- If \(|T|\geq \color{red}{t_\alpha}\), we reject \(H_0\) with confidence level \(1-\color{red}{\alpha}\).
- If \(|T|< \color{red}{t_\alpha}\), we CANNOT \(H_0\) due to insufficient evidence.

Summary
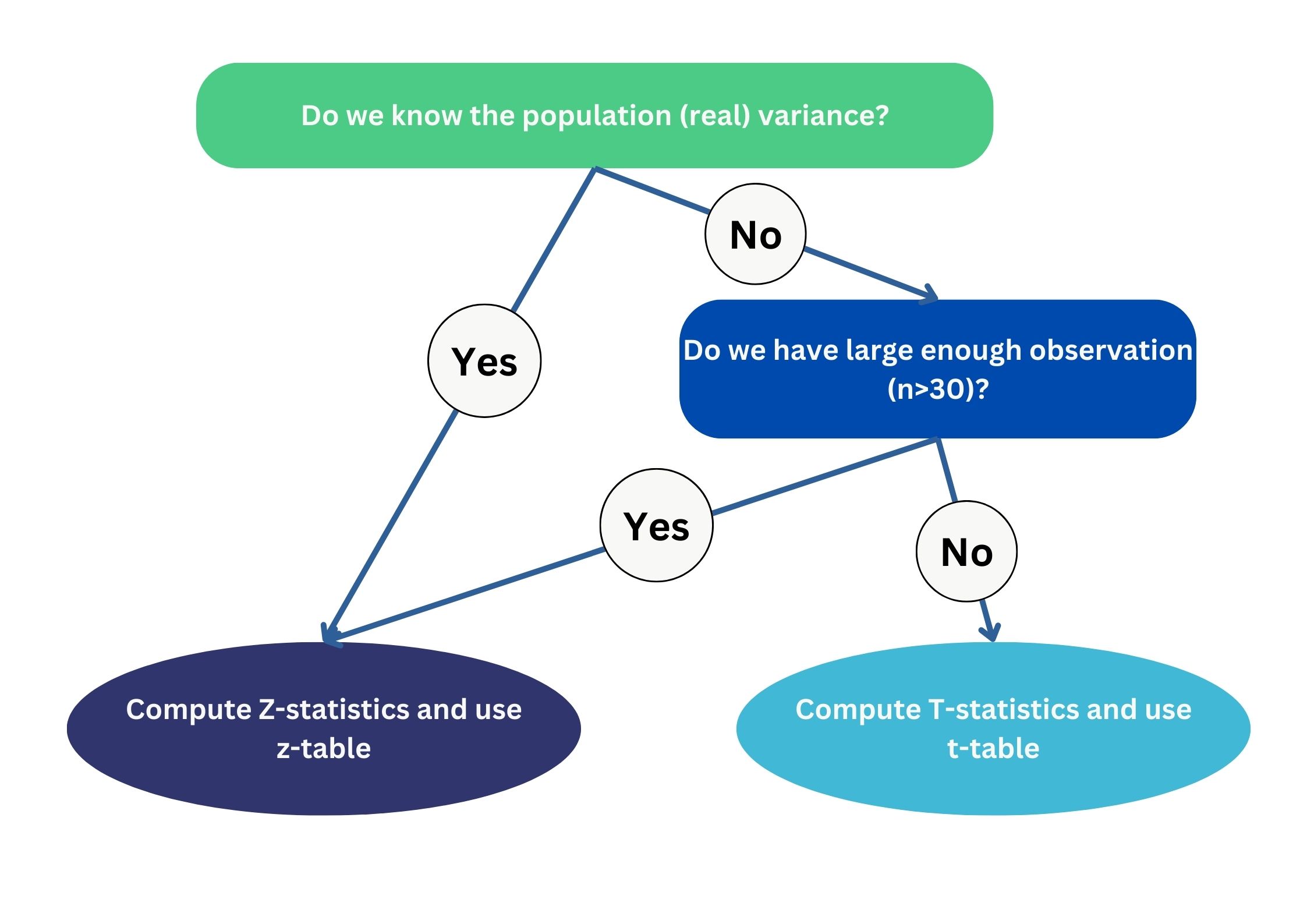
🥳 Yeahhhh….
Let’s Party… 🥂
