Categorical Analysis & \(\chi^2\)-test


INF-604: Data Analysis

Lecturer: Dr. Sothea HAS

Outline

  • Motivation

  • Contingency Table

  • \(\chi^2\)-Distance

  • \(\chi^2\)-Test

  • Application

Motivation

Motivation

Hair-Eye Color Dataset

  • Frequency table:
Code 
import pandas as pd
data = pd.read_csv(
    path_eye + "HairEyeColor.csv")\
    .drop(columns = ['Unnamed: 0'])
data
Hair Eye Sex Freq
0 Black Brown Male 32
1 Brown Brown Male 53
2 Red Brown Male 10
3 Blond Brown Male 3
4 Black Blue Male 11
5 Brown Blue Male 50
6 Red Blue Male 10
7 Blond Blue Male 30
8 Black Hazel Male 10
9 Brown Hazel Male 25
10 Red Hazel Male 7
11 Blond Hazel Male 5
12 Black Green Male 3
13 Brown Green Male 15
14 Red Green Male 7
15 Blond Green Male 8
16 Black Brown Female 36
17 Brown Brown Female 66
18 Red Brown Female 16
19 Blond Brown Female 4
20 Black Blue Female 9
21 Brown Blue Female 34
22 Red Blue Female 7
23 Blond Blue Female 64
24 Black Hazel Female 5
25 Brown Hazel Female 29
26 Red Hazel Female 7
27 Blond Hazel Female 5
28 Black Green Female 2
29 Brown Green Female 14
30 Red Green Female 7
31 Blond Green Female 8
  • Possible investigation:
    • Hair color vs Eye color
    • Gender vs Hair color
    • Gender vs Eye color
  • Let’s analyze Hair vs Eye color!
  • Q1: How to work with such a dataset?
  • A1: To analyze relationship between categorical variables, we often use contingency table.

Contingency Table

Contingency Table

  • To obtain a two-way contingency table (Hair vs Eye) from a three-way one, we sum over the Gender because: \[n(\text{H, E})=\sum_{x\in\{M,F\}}n(\text{H, E, G}=x).\]
Code 
df_hair_eye = data.pivot_table(
    values="Freq", 
    index="Hair", 
    columns="Eye", 
    aggfunc="sum", 
    fill_value=0)
Observed = df_hair_eye.copy()
n = df_hair_eye.sum().sum()
df_hair_eye
Eye Blue Brown Green Hazel
Hair
Black 20 68 5 15
Blond 94 7 16 10
Brown 84 119 29 54
Red 17 26 14 14
  • Does it look like there’s a relationship between Hair and Eye color?
  • Visualization:
Code 
import matplotlib.pyplot as plt
df_hair_eye.plot(kind="bar", figsize=(5, 3), width=0.8)
plt.title("Grouped Bar Chart of Hair vs. Eye Color")
plt.xlabel("Hair Color")
plt.ylabel("Frequency")
plt.legend(title="Eye Color")
plt.show()

  • How about now?
  • Goal: Establish statistical evidence to determine whether an association exists between 2 categorical variables.

Contingency Table

Marginal Frequency/ Relative Frequency

Eye Blue Brown Green Hazel
Hair
Black 20 68 5 15
Blond 94 7 16 10
Brown 84 119 29 54
Red 17 26 14 14
  • Let \(n_{i,j}\) be the joint frequency.
  • Marginal frequency:
    • Row freq: \(\color{blue}{n_{i,.}=\sum_{j=1}^Jn_{i,j}}.\)
    • Column freq: \(\color{red}{n_{.,j}=\sum_{i=1}^In_{i,j}}.\)

Contingency Table

Marginal Frequency/ Relative Frequency

Eye Blue Brown Green Hazel n_i
Hair
Black 20 68 5 15 108
Blond 94 7 16 10 127
Brown 84 119 29 54 286
Red 17 26 14 14 71
n_j 215 220 64 93 592
  • Let \(n_{i,j}\) be the joint frequency.
  • Marginal frequency:
    • Row freq: \(\color{blue}{n_{i,.}=\sum_{j=1}^Jn_{i,j}}.\)
    • Column freq: \(\color{red}{n_{.,j}=\sum_{i=1}^In_{i,j}}.\)

Contingency Table

Marginal Frequency/ Relative Frequency

Eye Blue Brown Green Hazel n_i
Hair
Black 20 68 5 15 108
Blond 94 7 16 10 127
Brown 84 119 29 54 286
Red 17 26 14 14 71
n_j 215 220 64 93 592
  • Let \(n_{i,j}\) be the joint frequency.
  • Marginal frequency:
    • Row freq: \(\color{blue}{n_{i,.}=\sum_{j=1}^Jn_{i,j}}.\)
    • Column freq: \(\color{red}{n_{.,j}=\sum_{i=1}^In_{i,j}}.\)
  • Joint relative frequency (JRF): \(\color{green}{p_{i,j}=n_{i,j}/N}\) with \(\color{green}{N=\sum_{i,j}n_{i,j}}\).
  • Marginal relative frequency (MRF):
    • Row RF: \(\color{blue}{p_{i,.}=n_{i,.}/N}\).
    • Column RF: \(\color{red}{p_{.,j}=n_{.,j}/N}\).

Contingency Table

Marginal Frequency/ Relative Frequency

Eye Blue Brown Green Hazel n_i p_i
Hair
Black 20.00 68.00 5.00 15.00 108.0 0.18
Blond 94.00 7.00 16.00 10.00 127.0 0.21
Brown 84.00 119.00 29.00 54.00 286.0 0.48
Red 17.00 26.00 14.00 14.00 71.0 0.12
n_j 215.00 220.00 64.00 93.00 592.0 1.00
p_j 0.36 0.37 0.11 0.16 1.0 NaN
  • Let \(n_{i,j}\) be the joint frequency.
  • Marginal frequency:
    • Row freq: \(\color{blue}{n_{i,.}=\sum_{j=1}^Jn_{i,j}}.\)
    • Column freq: \(\color{red}{n_{.,j}=\sum_{i=1}^In_{i,j}}.\)
  • Joint relative frequency (JRF): \(\color{green}{p_{i,j}=n_{i,j}/N}\) with \(\color{green}{N=\sum_{i,j}n_{i,j}}\).
  • Marginal relative frequency (MRF):
    • Row RF: \(\color{blue}{p_{i,.}=n_{i,.}/N}\).
    • Column RF: \(\color{red}{p_{.,j}=n_{.,j}/N}\).
  • Some key questions:
    • By assuming Hair \(\!\perp\!\!\!\perp\) Eye, compute:
      • \(\mathbb{P}(\text{Hair='Black', Eye=}\color{brown}{\text{'Brown'}})\)?
      • \(\mathbb{P}(\text{Hair=}\color{red}{\text{'Red'}}, \text{Eye=}\color{blue}{\text{'Blue'}})\)?
      • \(\mathbb{P}(\text{Hair=}\color{orange}{\text{'Blond'}}, \text{Eye=}\color{olive}{\text{'Hazel'}})\)?

Contingency Table

Expected vs Observed Contingency Table

  • If hair and eye are truly independent, then we expect the following contingency table: \[E_{ij}=p_{i,.}p_{.,j}N\]
Eye Blue Brown Green Hazel
Hair
Black 35.52 41.44 11.84 17.76
Blond 47.36 47.36 11.84 17.76
Brown 100.64 106.56 29.60 47.36
Red 23.68 23.68 5.92 11.84
  • This’s called ‘Expected contingency table’.
  • In reality, we observed:
Eye Blue Brown Green Hazel
Hair
Black 20 68 5 15
Blond 94 7 16 10
Brown 84 119 29 54
Red 17 26 14 14
  • It’s called ‘Observed contingency table’.
  • Q2: If Hair and Eye are independent, what can we say about these two table?
  • A2: They should be very similar!
  • We need a tool to measure the similarity between these two tables.

\(\chi^2\)-Distance

\(\chi^2\)-Distance

Measurement of similarity

  • Expected table:
Eye Blue Brown Green Hazel
Hair
Black 35.52 41.44 11.84 17.76
Blond 47.36 47.36 11.84 17.76
Brown 100.64 106.56 29.60 47.36
Red 23.68 23.68 5.92 11.84
  • Observed table:
Eye Blue Brown Green Hazel
Hair
Black 20 68 5 15
Blond 94 7 16 10
Brown 84 119 29 54
Red 17 26 14 14
  • \(\chi^2\)-distance between an Expected and an Observed table is defined by \[\chi^2=\sum_{i,j}\frac{(\color{blue}{E_{ij}}-\color{red}{O_{ij}})^2}{\color{blue}{E_{ij}}},\]
    • \(\color{blue}{E_{ij}}:\) expected frequency,
    • \(\color{red}{O_{ij}}:\) observed frequency.
  • For Hair and Eye example:
chi2_val = ((expect - Observed) ** 2/expect).sum().sum()
print(f"\nChi-squared distance: {np.round(chi2_val, 3)}")

Chi-squared distance: 132.043
  • Now, is this small or large?

\(\chi^2\)-Test

\(\chi^2\)-Test

Test of independence

  • Just like \(\color{blue}{z}\)-value and \(\color{red}{t}\)-value, \(\chi^2\)-distance follows a certain pattern if the two tables are independent.
  • This leads to the following hypothesis testing.

\(\chi^2\)-test

  • Let \(X\) and \(Y\) be two categorical variables (Hair and Eye, for example).
  • Goal: Testing \(H_0: X\!\perp\!\!\!\perp Y\) against \(H_1: X\not\!\perp\!\!\!\perp Y\) at significance level \(\alpha\).
  • Assumptions:
    • Observations are independent
    • Expected frequencies \(E_{ij}\geq 1\) and more than \(20\%\) are larger than \(5\).
  • Key result: Under \(H_0\) is true, then \(\chi^2\sim\color{blue}{\chi^2((I-1)(J-1))}\), the chi-squared distribution of DF \(=(I-1)(J-1)\).
  • We reject \(H_0\) if \(\chi^2\geq \color{red}{c_{\alpha}}\) where \(\color{red}{c_{\alpha}}\) s.t: \(\mathbb{P}(\color{blue}{\chi^2((I-1)(J-1))}\geq \color{red}{c_{\alpha}})=\color{red}{\alpha}\).
Code 
import plotly.graph_objects as go
from scipy.stats import chi2

# Create x-axis values (domain for chi-squared)
x = np.linspace(0, 50, 100)

# Degrees of freedom to display
dfs = [1, 5, 10, 15, 20, 30]

# Create figure
fig = go.Figure()

# Add trace for each degree of freedom
for df in dfs:
    y = chi2.pdf(x, df)
    
    # Add line to plot
    fig.add_trace(
        go.Scatter(
            x=x,
            y=y,
            mode='lines',
            name=f'df = {df}',
            line=dict(width=2)
        )
    )

# Update layout
fig.update_layout(
    title=r'$\chi^2(\text{df})$',
    xaxis_title='x',
    yaxis_title='Density',
    legend_title='DFs',
    template='plotly_white',
    hovermode='closest',
    width=240,
    height=180
)

fig.show()

\(\chi^2\)-Test

Test of independence

Summary \(\chi^2\)-test

  • Compute \(\chi^2\)-distance value \(\chi^2\).
  • For a given significance level \(\color{red}{\alpha}\) (for example, \(0.05\)), compute \(\color{blue}{\text{df}=(I-1)(J-1)}\), then:
    • Critical value method: Look at the table of \(\color{blue}{\chi^2(\text{df})}\) to find \(\color{red}{c_{\alpha}}\). Decision: Reject \(H_0\) if \(\chi^2\geq \color{red}{c_{\alpha}}\).
    • P-value method: Compute \(\text{p-value}=\mathbb{P}(\color{blue}{\chi^2(\text{df})}\geq \chi^2)\). Decision: Reject \(H_0\) if \(\text{p-value}< \color{red}{\alpha}\).


  • For our example: \(\chi^2=\) 132.043, let’s take \(\color{red}{\alpha=0.01}\).
  • DF = \((I-1)(J-1)=(4-1)(4-1)=9\)
  • Critical value: if \(\mathbb{P}(\color{blue}{\chi^2(9)}\geq \color{red}{c_{0.05}})=0.01\Rightarrow \color{red}{c_{0.01}}=\) 21.67.
  • Or we can compute p-value \(=\mathbb{P}(\color{blue}{\chi^2(9)}\geq\) 132.043 \()\approx\) 0.0.
  • Both leads to rejection of \(H_0\). Conclusion: With confidence level \(>99.99\%\), Hair and Eye colors are related.

Applications

Applications

Detecting informative inputs

male age education currentSmoker cigsPerDay BPMeds prevalentStroke prevalentHyp diabetes totChol sysBP diaBP BMI heartRate glucose TenYearCHD
0 1 39 4.0 0 0.0 0.0 0 0 0 195.0 106.0 70.0 26.97 80.0 77.0 0
1 0 46 2.0 0 0.0 0.0 0 0 0 250.0 121.0 81.0 28.73 95.0 76.0 0
2 1 48 1.0 1 20.0 0.0 0 0 0 245.0 127.5 80.0 25.34 75.0 70.0 0
3 0 61 3.0 1 30.0 0.0 0 1 0 225.0 150.0 95.0 28.58 65.0 103.0 1
4 0 46 3.0 1 23.0 0.0 0 0 0 285.0 130.0 84.0 23.10 85.0 85.0 0
  • Who ignored the relationship between qualitative columns with the target TenYearCHD 🤔?

  • What graph can be used to visualize such relationships?
  • Yes, grouped barplots or mosaic plots!
  • \(\chi^2\)-test can be used to detect this type of connection.

Applications

Detecting informative inputs

  • Perform \(\chi^2\)-test of the target vs all qualitative inputs:
Code 
def chi2_independence_test(observed_data):
    if isinstance(observed_data, pd.DataFrame):
        observed_data = observed_data.values
    
    observed = np.array(observed_data)
    
    row_totals = observed.sum(axis=1, keepdims=True)
    col_totals = observed.sum(axis=0, keepdims=True)
    total = observed.sum()
    expected = np.dot(row_totals, col_totals) / total
    dof = (observed.shape[0] - 1) * (observed.shape[1] - 1)
    chi2_stat = np.sum((observed - expected) ** 2 / expected)
    p_value = 1 - chi2.cdf(chi2_stat, dof)
    return chi2_stat, p_value, dof, expected
tab_result = pd.DataFrame([], 
    columns=['Chi2-stat', 'df', 'p-value'])
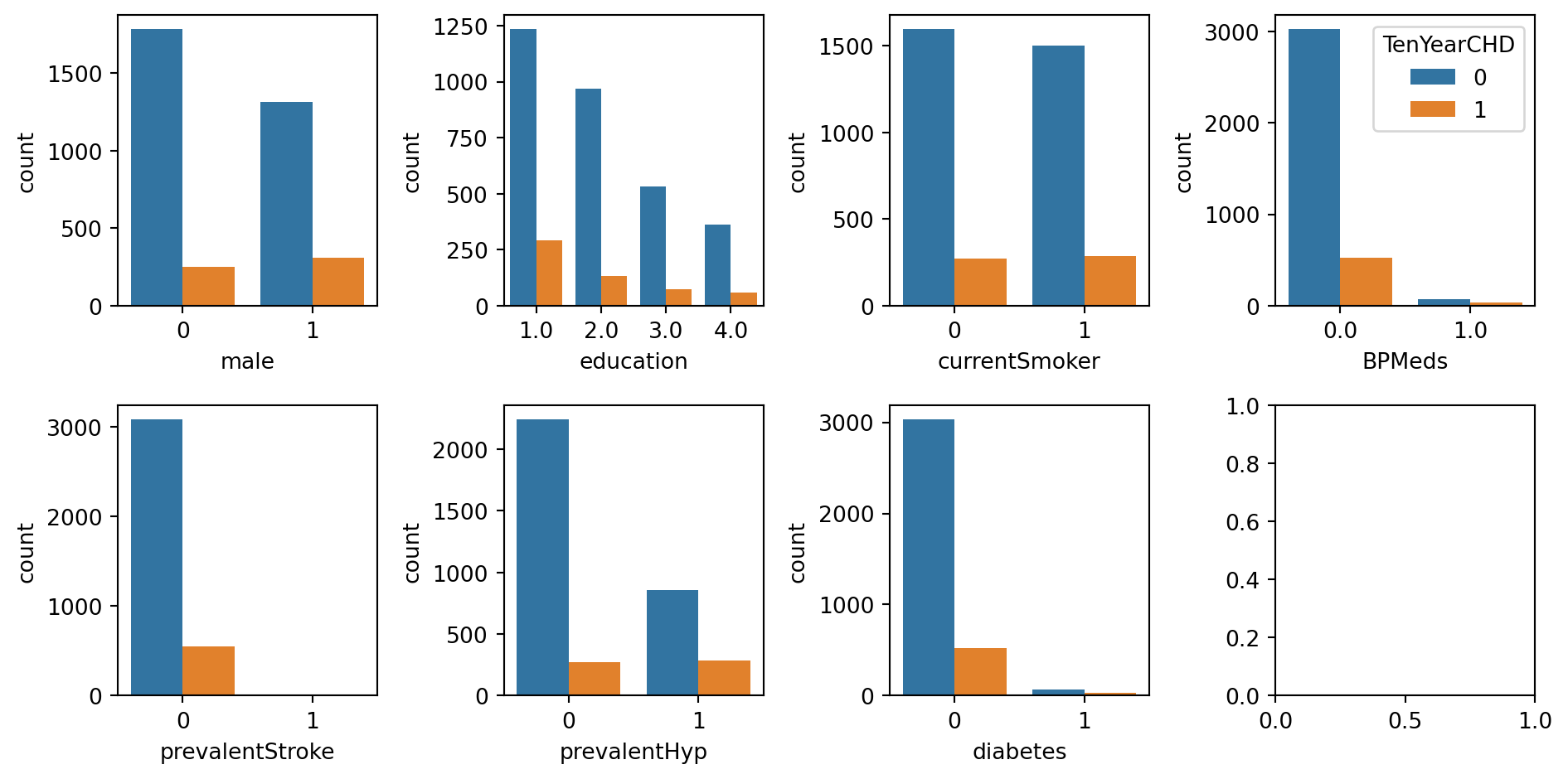
for va in qual_var[:-1]:
    tab = pd.crosstab(data_cleaned[va], data_cleaned['TenYearCHD'])
    chi2_stat, p_value, dof, expected = chi2_independence_test(tab)
    tab_result = pd.concat([tab_result, 
                pd.DataFrame({ 
                    'Chi2-stat': chi2_stat, 
                    'df': dof, 
                    'p-value': p_value}, index=[va])], axis=0)
tab_result.index = qual_var[:-1]
tab_result
Chi2-stat df p-value
male 30.773005 1 2.900448e-08
education 31.062637 3 8.246211e-07
currentSmoker 1.344408 1 2.462581e-01
BPMeds 29.034521 1 7.109993e-08
prevalentStroke 8.546916 1 3.461081e-03
prevalentHyp 120.511730 1 0.000000e+00
diabetes 31.891572 1 1.630230e-08

Applications

Detecting informative inputs

  • Visualization:

Summary

  • \(\chi^2\)-distance can be used to measure similarity between expected and observed contingency table.
  • \(\chi^2\)-test can be used to detect the relationship between two categorical variables, but make sure the two assumptions are satisfied:
    • Independency of observations.
    • Significantly large expected frequency (> 5).
  • It can be used to summarize the connection between categorical inputs with categorical target before building classification models.
  • Remark: categorical inputs are as important as the numerical ones, don’t ignore them.

🥳 Yeahhhh….









Let’s Party… 🥂