🗺️ Content
Motivation & Tools
Bagging: Random Forest
Boosting: Adaboost, XGBoost…
Concensual aggregation: COBRA, KernelCOBRA, MixCOBRA
Stacking: SuperLearner
AMSI61AML
Motivation & Tools
Bagging: Random Forest
Boosting: Adaboost, XGBoost…
Concensual aggregation: COBRA, KernelCOBRA, MixCOBRA
Stacking: SuperLearner
🤔 Have you ever thought about:
Why do we trust a panel of judges more than a single judge in competitions?
In medicine, why do doctors often seek second or third opinions for complex cases?
Have you noticed that weather forecasts often give a probability of rain rather than a simple yes/no prediction?
Would the famous “Wisdom of Crowds” principle applies to machine learning?
Bagging: Combine nearly decorrelated high-varianced models.
Boosting: Sequentially combine weak learners.
Stacking: Combination is based on the predicted features.
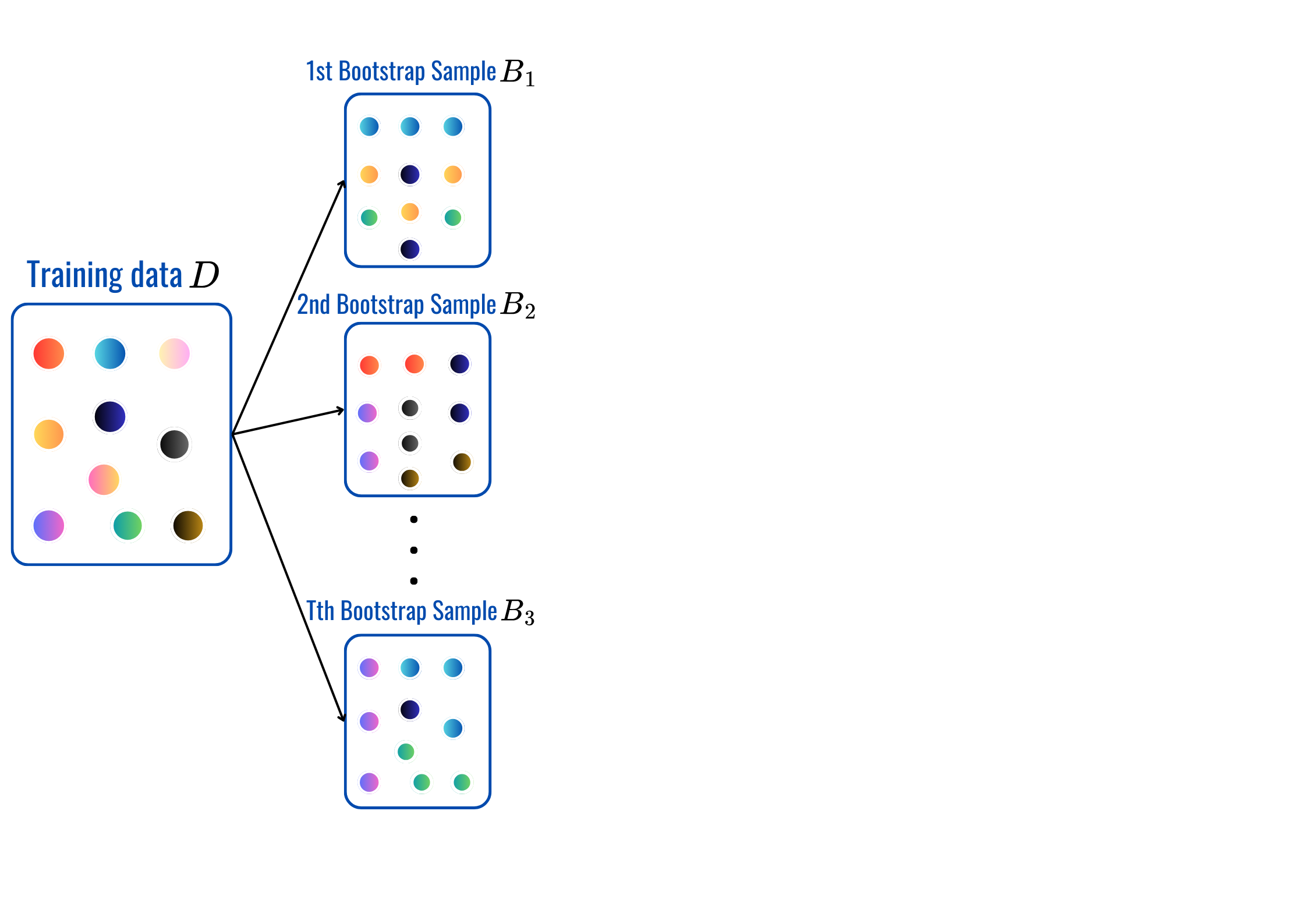
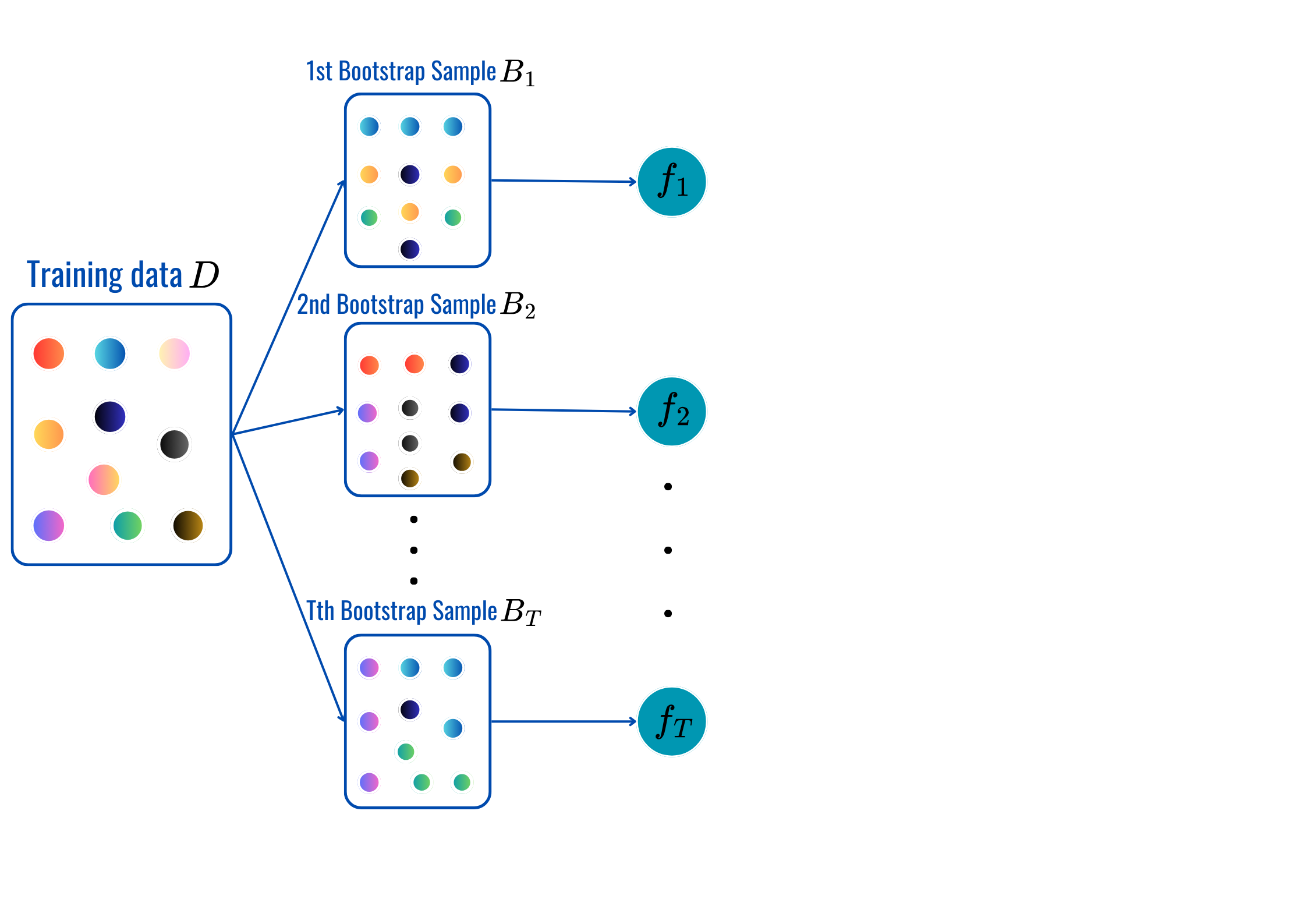
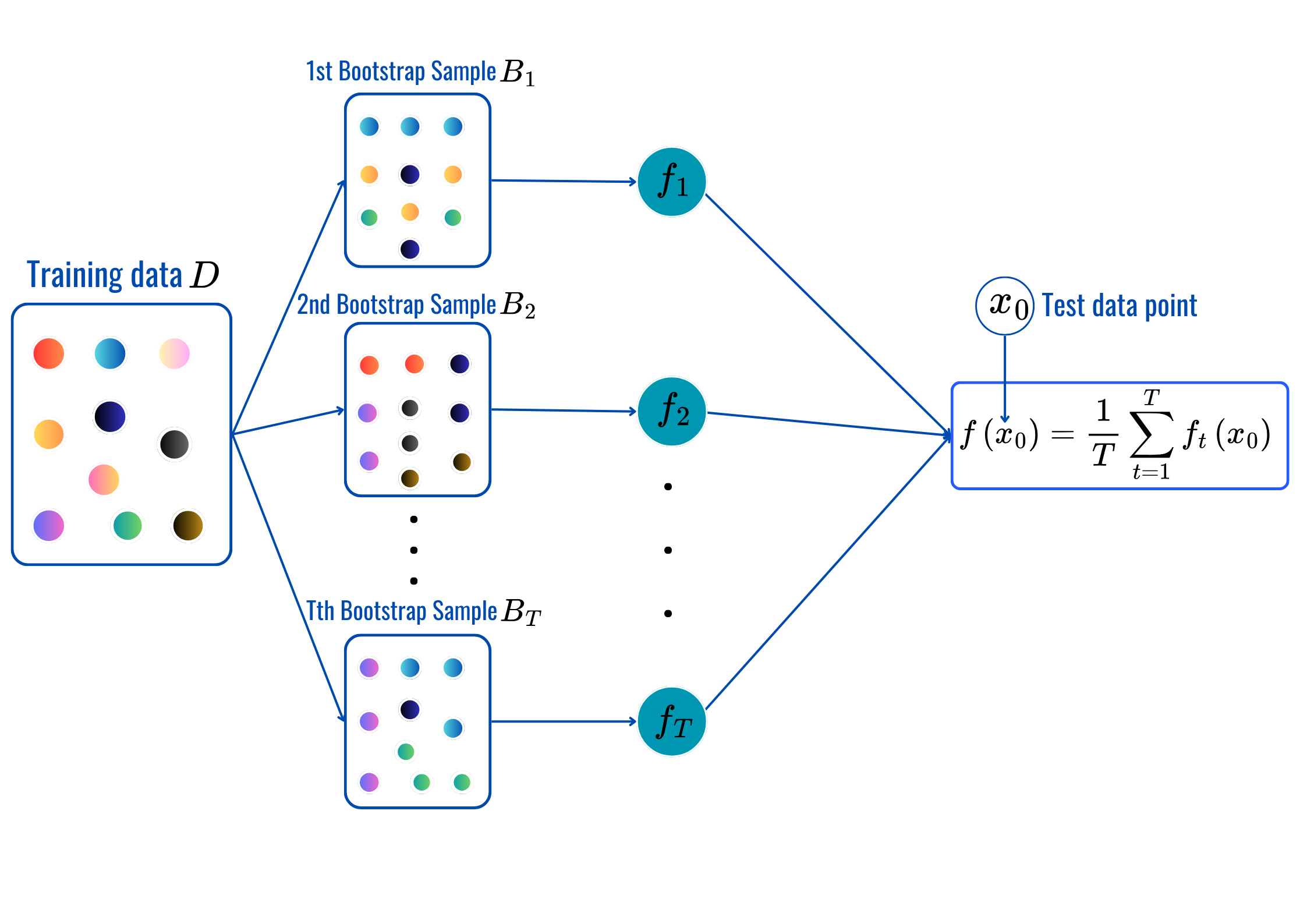
for t=1,...,T:
Predictions:
Bias-variance trade-off: Assuming \(y_i=f(\text{x}_i)+\varepsilon_i\) where \(\varepsilon_i\overset{iid}{\sim}{\cal N}(0,\sigma^2)\), then for any model \(\hat{f}\) built using training data \(\cal D\), we can decompose MSE of \(\hat{f}\) at any fixed input \(\text{x}_0\) as \[\begin{align*} \mathbb{E}_{\cal D}[(\hat{f}(\text{x}_0)-y_0)^2]&=\mathbb{E}_{\cal D}[(\hat{f}(\text{x}_0)-\mathbb{E}[\hat{f}(\text{x}_0)])^2] + \mathbb{E}_{\cal D}[(\mathbb{E}[\hat{f}(\text{x}_0)]-f(\text{x}_0))^2] + \sigma^2\\ &=\underbrace{\mathbb{V}(\hat{f}(\text{x}_0))}_{\color{blue}{\text{Flexibility of }\hat{f}}}+\underbrace{(\text{Bias})^2}_{\color{darkgreen}{\text{How far }\hat{f}\text{ from } f}}+\underbrace{\sigma^2}_{\color{red}{\text{Uncontrollable Term}}}. \end{align*}\]
Begging: seeks to balance these terms by averaging nearly independent high-varianced models to reduce more stable predictive model.
for t = 1,2,...,T:
Prediction: (same as before).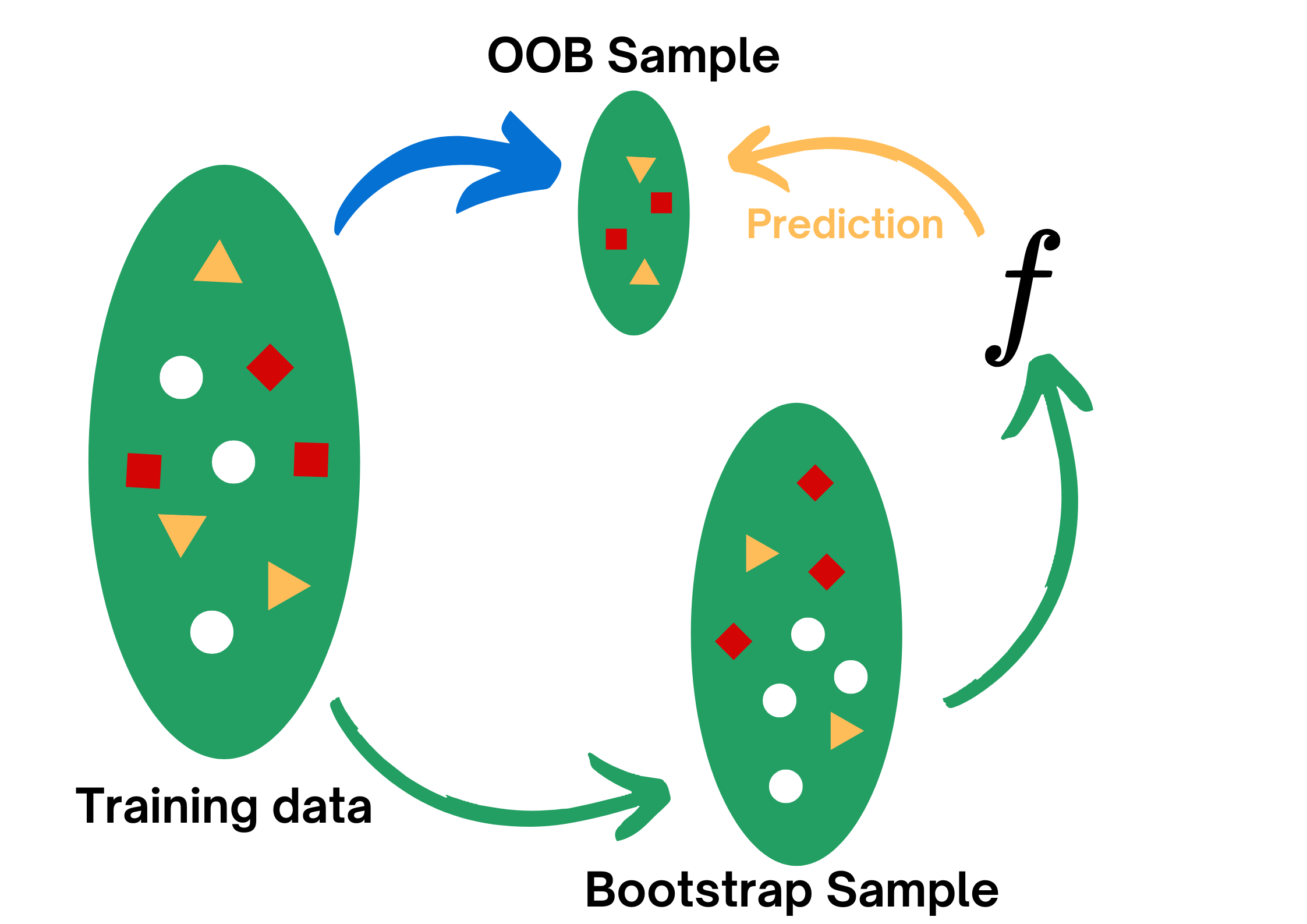
for t = 1,2,...,T:
Prediction: (same as before).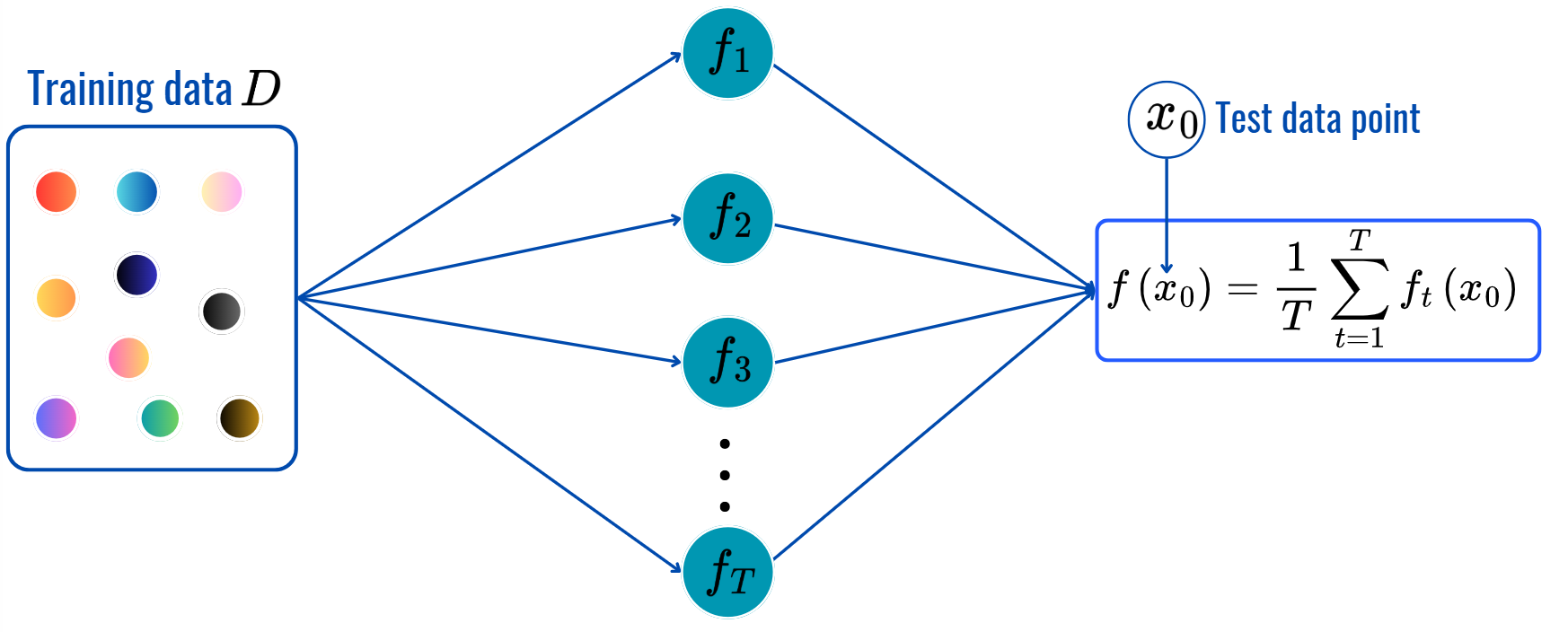
| Sex | Length | Diameter | Height | Whole weight | Shucked weight | Viscera weight | Shell weight | Rings | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | M | 0.455 | 0.365 | 0.095 | 0.5140 | 0.2245 | 0.1010 | 0.150 | 15 |
| 1 | M | 0.350 | 0.265 | 0.090 | 0.2255 | 0.0995 | 0.0485 | 0.070 | 7 |
| 2 | F | 0.530 | 0.420 | 0.135 | 0.6770 | 0.2565 | 0.1415 | 0.210 | 9 |
| 3 | M | 0.440 | 0.365 | 0.125 | 0.5160 | 0.2155 | 0.1140 | 0.155 | 10 |
| 4 | I | 0.330 | 0.255 | 0.080 | 0.2050 | 0.0895 | 0.0395 | 0.055 | 7 |
👉 Check out the notebook.
for t = 1, 2,..., T:



for t = 1, . . . , T:
for t = 1, 2, ..., M:
\[\begin{align*}L(F_t)&=\sum_{i=1}^nL(y_i,F_t(\text{X}_i))+\sum_{m=1}^t\Omega(f_m)\\ \Omega(f_t)&=\gamma T+\frac{1}{2}\lambda\|w\|^2.\\ L(F_t)&\approx \sum_{i=1}^n[g_iF_t(\text{x}_i)+\frac{1}{2}h_iF_t^2(\text{x}_i)]+\Omega(F_t),\\ g_i&=\frac{\partial L(y_i,F_t(\text{x}))}{\partial F_t(\text{x})}\|_{F_t(\text{x})=F_t(\text{x}_i)}\\ h_i&=\frac{\partial^2 L(y_i,F_t(\text{x}))}{\partial F_t(\text{x})^2}\|_{F_t(\text{x})=F_t(\text{x}_i)}. \end{align*}\]
to ensure the efficiency and accuracy of the method.
👉 Check out the notebook.
\[\text{x}_i\overset{f_1,\dots,f_M}{\mapsto}\color{red}{\widehat{\text{x}}=(f_1(\text{x}),\dots,f_M(\text{x}))}\mapsto \hat{y}=\sum_{i=1}^nW_{n,i}(\color{red}{\widehat{\text{x}}})y_i.\]
| Id | \(C_1\) | \(C_2\) | \(C_3\) | \(Y\) |
|---|---|---|---|---|
| 1 | \(0\) | \(1\) | \(1\) | \(1\) |
| 2 | 1 | 1 | 0 | \(\color{blue}{1}\) |
| 3 | \(0\) | \(0\) | \(0\) | \(0\) |
| 4 | 1 | 1 | 0 | \(\color{blue}{1}\) |
| 5 | 1 | 1 | 0 | \(\color{red}{0}\) |
| \(\text{x}\) | 1 | 1 | 0 | \(?\) |
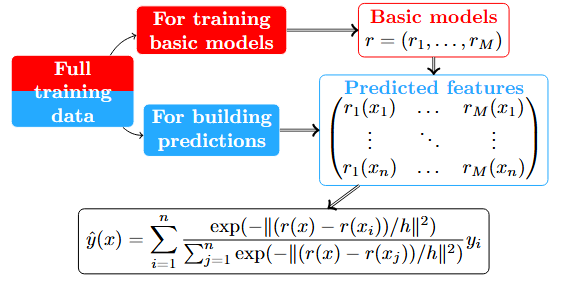
\[\varphi(h)=\frac{1}{K}\sum_{k=1}^K\sum_{(\text{x}_i,y_i)\in F_j}(\hat{y}_i-y_i)^2.\]


\[\varphi(\alpha,\beta)=\frac{1}{K}\sum_{k=1}^K\sum_{(\text{x}_i,y_i)\in F_j}(\hat{y}_i-y_i)^2.\]

👉 Check out the notebook.
\[\text{x}_i\overset{f_1,\dots,f_M}{\mapsto}\color{red}{\widehat{\text{x}_i}=(f_1(\text{x}_i),\dots,f_M(\text{x}_i))}\overset{\text{Meta-learner }f}{\mapsto} \hat{y}_i=f(\color{red}{\widehat{x}_i}).\]
👉 Check out the notebook.
Ensemble learning: combine base learners to create a stronger predictor.
Bagging: Combines high-varianced base learners (trees) to produce a more stable and accurate final model.
Boosting: Sequentially combines weak learners aiming at correcting mistakes made by the previous built combined learners to create a strong model.
Consensual Aggregation: Combine different learners using the consensuses of their predicted features.
Stacking: Build meta-learners using predicted features of base learners to predict the target.
