Ensemble Learning

Abalone dataset

The dataset is available here: https://www.kaggle.com/datasets/rodolfomendes/abalone-dataset.

import kagglehub

# Download latest version
path = kagglehub.dataset_download("rodolfomendes/abalone-dataset")

# Import data
import pandas as pd
data = pd.read_csv(path + "/abalone.csv")
data.head()
Warning: Looks like you're using an outdated `kagglehub` version (installed: 0.3.6), please consider upgrading to the latest version (0.3.7).
Sex Length Diameter Height Whole weight Shucked weight Viscera weight Shell weight Rings
0 M 0.455 0.365 0.095 0.5140 0.2245 0.1010 0.150 15
1 M 0.350 0.265 0.090 0.2255 0.0995 0.0485 0.070 7
2 F 0.530 0.420 0.135 0.6770 0.2565 0.1415 0.210 9
3 M 0.440 0.365 0.125 0.5160 0.2155 0.1140 0.155 10
4 I 0.330 0.255 0.080 0.2050 0.0895 0.0395 0.055 7 
print(f"Number of rows: {data.shape[0]}")
print(f"Number of columns: {data.shape[1]}")
Number of rows: 4177
Number of columns: 9

1. EDA

# Data types
data.dtypes
Sex                object
Length            float64
Diameter          float64
Height            float64
Whole weight      float64
Shucked weight    float64
Viscera weight    float64
Shell weight      float64
Rings               int64
dtype: object
data.describe()
Length Diameter Height Whole weight Shucked weight Viscera weight Shell weight Rings
count 4177.000000 4177.000000 4177.000000 4177.000000 4177.000000 4177.000000 4177.000000 4177.000000
mean 0.523992 0.407881 0.139516 0.828742 0.359367 0.180594 0.238831 9.933684
std 0.120093 0.099240 0.041827 0.490389 0.221963 0.109614 0.139203 3.224169
min 0.075000 0.055000 0.000000 0.002000 0.001000 0.000500 0.001500 1.000000
25% 0.450000 0.350000 0.115000 0.441500 0.186000 0.093500 0.130000 8.000000
50% 0.545000 0.425000 0.140000 0.799500 0.336000 0.171000 0.234000 9.000000
75% 0.615000 0.480000 0.165000 1.153000 0.502000 0.253000 0.329000 11.000000
max 0.815000 0.650000 1.130000 2.825500 1.488000 0.760000 1.005000 29.000000
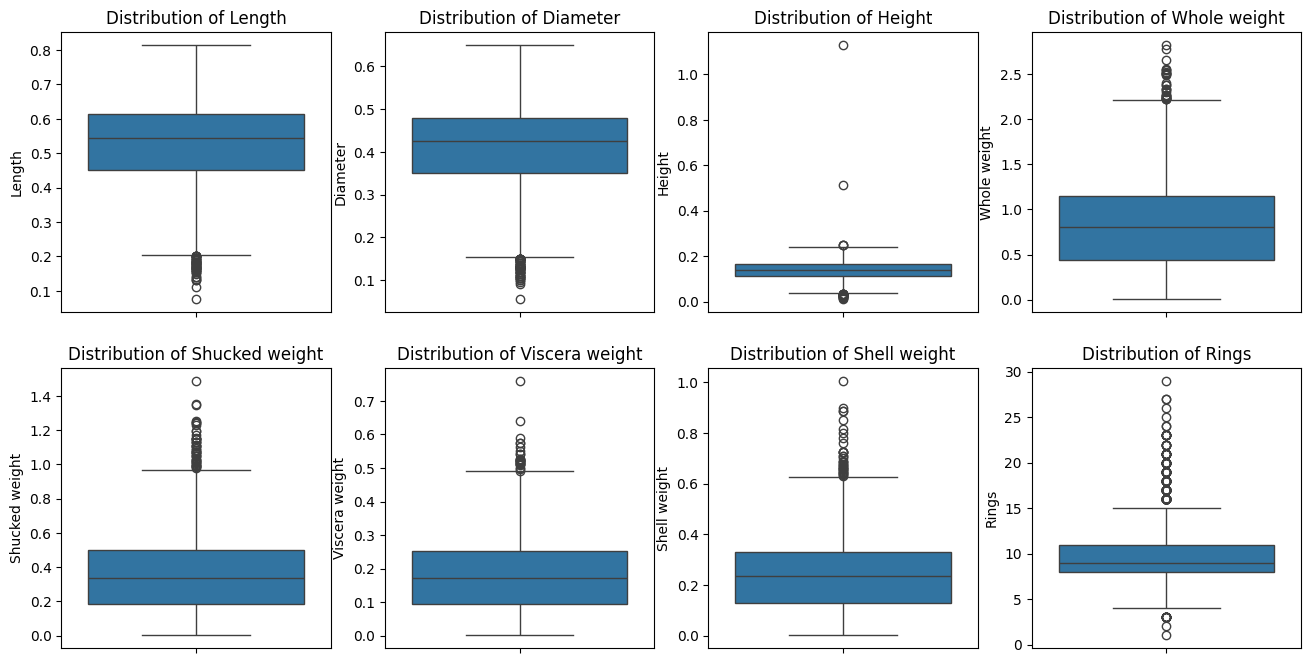
  • There are missing values (abalone with 0 heights). We shall handle this.
data = data.loc[data.Height > 0]
data.describe()
Length Diameter Height Whole weight Shucked weight Viscera weight Shell weight Rings
count 4175.000000 4175.00000 4175.000000 4175.000000 4175.000000 4175.000000 4175.000000 4175.000000
mean 0.524065 0.40794 0.139583 0.829005 0.359476 0.180653 0.238834 9.935090
std 0.120069 0.09922 0.041725 0.490349 0.221954 0.109605 0.139212 3.224227
min 0.075000 0.05500 0.010000 0.002000 0.001000 0.000500 0.001500 1.000000
25% 0.450000 0.35000 0.115000 0.442250 0.186250 0.093500 0.130000 8.000000
50% 0.545000 0.42500 0.140000 0.800000 0.336000 0.171000 0.234000 9.000000
75% 0.615000 0.48000 0.165000 1.153500 0.502000 0.253000 0.328750 11.000000
max 0.815000 0.65000 1.130000 2.825500 1.488000 0.760000 1.005000 29.000000 
print(f'Number of duplicated data: {data.duplicated().sum()}')
Number of duplicated data: 0

1.1 Univariate Analysis

import seaborn as sns
import matplotlib.pyplot as plt
import plotly.express as px

quan_cols = data.select_dtypes(include="number").columns
_, axs = plt.subplots(2,4, figsize=(16, 8))
for i, va in enumerate(quan_cols):
  sns.boxplot(data=data, y=va, ax=axs[i//4, i % 4])
  axs[i//4, i % 4].set_title(f"Distribution of {va}")
plt.show()

sns.countplot(data=data, x="Sex")
plt.show()

1.2 Bivariate Analysis

data.select_dtypes(include='number').corr()
Length Diameter Height Whole weight Shucked weight Viscera weight Shell weight Rings
Length 1.000000 0.986802 0.828108 0.925217 0.897859 0.902960 0.898419 0.556464
Diameter 0.986802 1.000000 0.834298 0.925414 0.893108 0.899672 0.906084 0.574418
Height 0.828108 0.834298 1.000000 0.819886 0.775621 0.798908 0.819596 0.557625
Whole weight 0.925217 0.925414 0.819886 1.000000 0.969389 0.966354 0.955924 0.540151
Shucked weight 0.897859 0.893108 0.775621 0.969389 1.000000 0.931924 0.883129 0.420597
Viscera weight 0.902960 0.899672 0.798908 0.966354 0.931924 1.000000 0.908186 0.503562
Shell weight 0.898419 0.906084 0.819596 0.955924 0.883129 0.908186 1.000000 0.627928
Rings 0.556464 0.574418 0.557625 0.540151 0.420597 0.503562 0.627928 1.000000 
data.select_dtypes(include='number').corr(method="spearman")
Length Diameter Height Whole weight Shucked weight Viscera weight Shell weight Rings
Length 1.000000 0.983299 0.888124 0.972600 0.956790 0.952600 0.948662 0.603954
Diameter 0.983299 1.000000 0.895651 0.971290 0.950422 0.948328 0.954896 0.622487
Height 0.888124 0.895651 1.000000 0.915963 0.874163 0.900535 0.922130 0.657403
Whole weight 0.972600 0.971290 0.915963 1.000000 0.977038 0.975222 0.970197 0.630440
Shucked weight 0.956790 0.950422 0.874163 0.977038 1.000000 0.947581 0.918465 0.538956
Viscera weight 0.952600 0.948328 0.900535 0.975222 0.947581 1.000000 0.938893 0.613930
Shell weight 0.948662 0.954896 0.922130 0.970197 0.918465 0.938893 1.000000 0.692991
Rings 0.603954 0.622487 0.657403 0.630440 0.538956 0.613930 0.692991 1.000000 
plt.figure(figsize=(16,16))
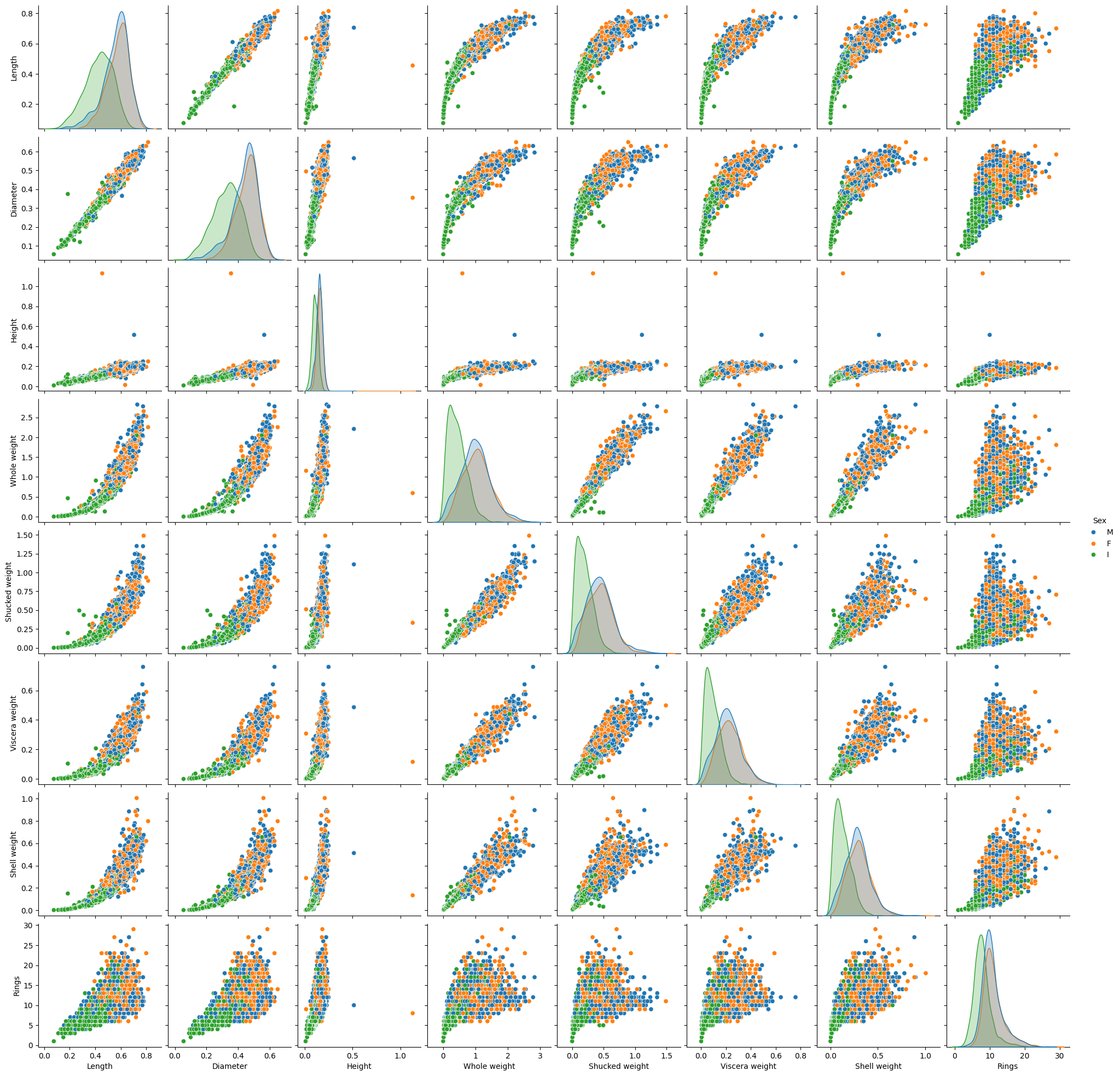
sns.pairplot(data=data, hue="Sex")
plt.show()
<Figure size 1600x1600 with 0 Axes>

Height has low correlation with the target Rings but this is likely due to the 2 weird data point with large height but small rings. One can remove these data points. Moreover the target spread widely at large values of inputs. One can scale the target to improve the connection.

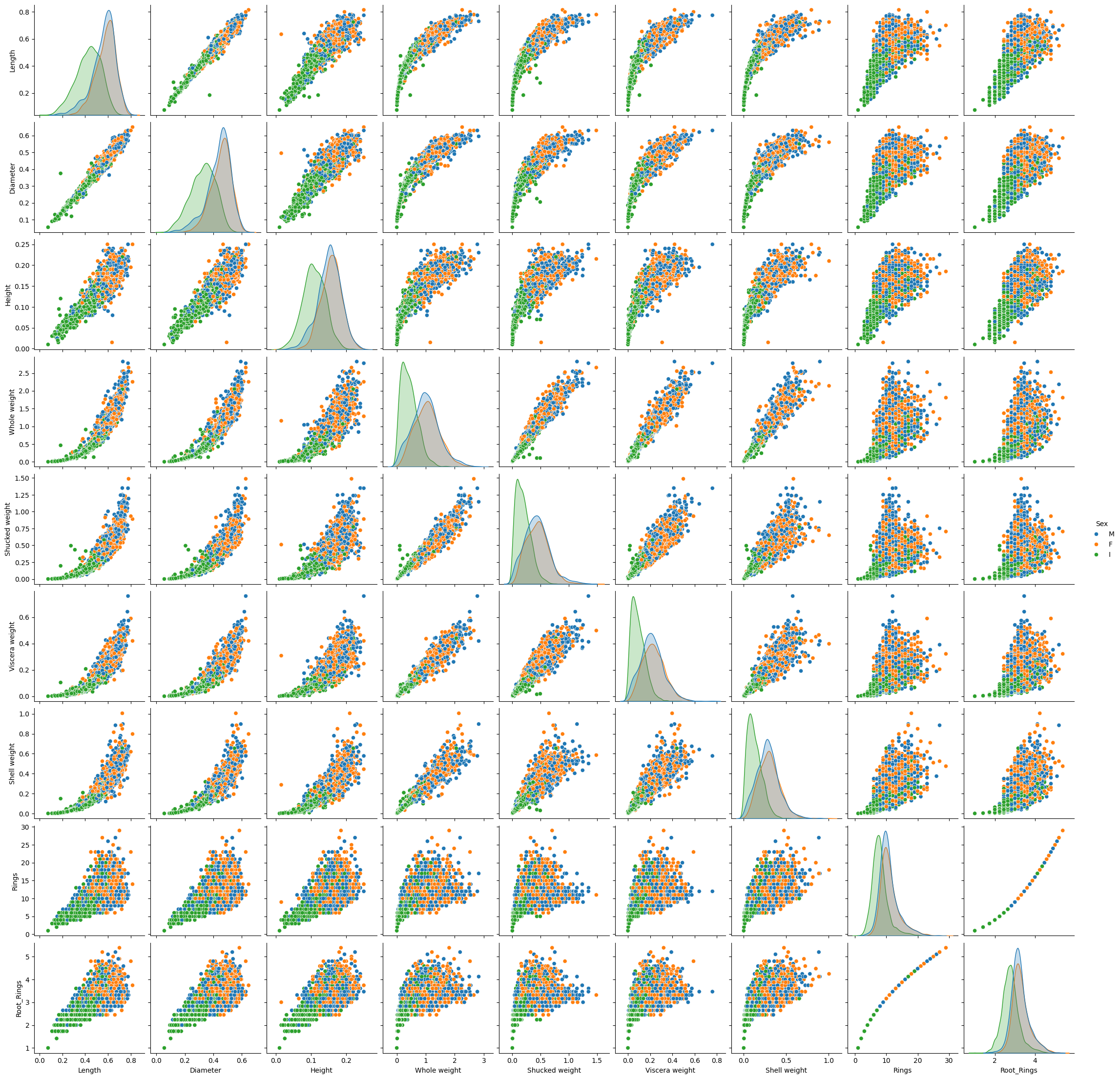
data1 = data
import numpy as np
data.drop(data[data['Height'] > 0.5].index, inplace=True)
data1['Root_Rings'] = data['Rings'].map(lambda x: np.sqrt(x))
sns.pairplot(data=data1, hue="Sex")
plt.show()

data1.drop(columns=['Sex']).corr()
Length Diameter Height Whole weight Shucked weight Viscera weight Shell weight Rings Root_Rings
Length 1.000000 0.986794 0.900868 0.925328 0.898129 0.903033 0.898363 0.556572 0.609433
Diameter 0.986794 1.000000 0.907187 0.925499 0.893330 0.899716 0.906026 0.574551 0.626043
Height 0.900868 0.907187 1.000000 0.888850 0.837485 0.866757 0.891857 0.610107 0.651990
Whole weight 0.925328 0.925499 0.888850 1.000000 0.969370 0.966290 0.955954 0.540621 0.574118
Shucked weight 0.898129 0.893330 0.837485 0.969370 1.000000 0.931831 0.883194 0.421156 0.460780
Viscera weight 0.903033 0.899716 0.866757 0.966290 0.931831 1.000000 0.908133 0.503977 0.540612
Shell weight 0.898363 0.906026 0.891857 0.955954 0.883194 0.908133 1.000000 0.628169 0.654175
Rings 0.556572 0.574551 0.610107 0.540621 0.421156 0.503977 0.628169 1.000000 0.991914
Root_Rings 0.609433 0.626043 0.651990 0.574118 0.460780 0.540612 0.654175 0.991914 1.000000 
data1.drop(columns=['Sex']).corr(method="spearman")
Length Diameter Height Whole weight Shucked weight Viscera weight Shell weight Rings Root_Rings
Length 1.000000 0.983282 0.888776 0.972587 0.956831 0.952555 0.948606 0.603924 0.603924
Diameter 0.983282 1.000000 0.896281 0.971271 0.950446 0.948276 0.954847 0.622477 0.622477
Height 0.888776 0.896281 1.000000 0.916451 0.874402 0.901073 0.922828 0.658139 0.658139
Whole weight 0.972587 0.971271 0.916451 1.000000 0.977044 0.975198 0.970182 0.630489 0.630489
Shucked weight 0.956831 0.950446 0.874402 0.977044 1.000000 0.947578 0.918476 0.539061 0.539061
Viscera weight 0.952555 0.948276 0.901073 0.975198 0.947578 1.000000 0.938835 0.613942 0.613942
Shell weight 0.948606 0.954847 0.922828 0.970182 0.918476 0.938835 1.000000 0.693018 0.693018
Rings 0.603924 0.622477 0.658139 0.630489 0.539061 0.613942 0.693018 1.000000 1.000000
Root_Rings 0.603924 0.622477 0.658139 0.630489 0.539061 0.613942 0.693018 1.000000 1.000000

2. Models

from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor, ExtraTreesRegressor
from sklearn.metrics import mean_squared_error

2.1 Bagging: Random Forest & Extra-Trees

import numpy as np
x_cat = pd.get_dummies(data["Sex"], drop_first=True)
X = pd.concat([x_cat, data.iloc[:,1:-1]], axis=1)
y = data['Rings'].map(lambda x: np.sqrt(x))
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=42)
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
(2921, 10) (2921,)
(1252, 10) (1252,)
rf = RandomForestRegressor(n_estimators=300)
rf.fit(X_train, y_train)
y_pred_rf = rf.predict(X_test)
print(f"RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_rf))}")
RMSE: 0.004429570403170732
ext = ExtraTreesRegressor(n_estimators=300)
ext.fit(X_train, y_train)
y_pred_ex = ext.predict(X_test)
print(f"RMSE: {np.sqrt(mean_squared_error(y_test, y_pred_ex))}")
RMSE: 0.002914711157601805
  • GridsearchCV Random Forest
from sklearn.model_selection import GridSearchCV

param_grid = {
    'n_estimators': [500, 800, 1000],
    'min_samples_leaf' : [2, 3, 5, 7, 10],
    'max_features' : np.linspace(5, X_train.shape[1], 3, dtype=int)
}

cv = GridSearchCV(
    estimator=RandomForestRegressor(),
    param_grid=param_grid, cv=5, 
    scoring='neg_mean_squared_error')
cv.fit(X_train, y_train)
rf_cv = RandomForestRegressor(**cv.best_params_).fit(X_train, y_train)
y_pred_rf_cv = rf_cv.predict(X_test)
rmse_rf_cv = np.sqrt(mean_squared_error(y_test, y_pred_rf_cv))
df_rmse = pd.DataFrame(
    {'RF_CV': [rmse_rf_cv]}
)
df_rmse
RF_CV
0 0.007523 
print(f'* Optimal parameter: {cv.best_params_}')
* Optimal parameter: {'max_features': 10, 'min_samples_leaf': 2, 'n_estimators': 500}
  • Extra-trees
cv = GridSearchCV(
    estimator=ExtraTreesRegressor(), 
    param_grid=param_grid, cv=5, 
    scoring='neg_mean_squared_error')
cv.fit(X_train, y_train)

ext_cv = ExtraTreesRegressor(**cv.best_params_).fit(X_train, y_train)
y_pred_ex_cv = ext_cv.predict(X_test)
rmse_ext_cv = np.sqrt(mean_squared_error(y_test, y_pred_ex_cv))
df_rmse = pd.concat([df_rmse, pd.DataFrame(
                    {'Extra-trees_CV': [rmse_ext_cv]})], 
                    axis=1)
df_rmse
RF_CV Extra-trees_CV
0 0.007523 0.005515 
print(f'* Optimal parameter: {cv.best_params_}')
* Optimal parameter: {'max_features': 10, 'min_samples_leaf': 2, 'n_estimators': 500}

2.2 Boosting: XGBoost

from xgboost.sklearn import XGBRegressor

xgb_model = XGBRegressor(objective="reg:squarederror")
xgb_model.fit(X_train, y_train)
y_pred_xgb = xgb_model.predict(X_test)
print(f"RMSE without CV: {np.sqrt(mean_squared_error(y_test, y_pred_xgb))}")
RMSE without CV: 0.005525182469075176

GridseachCV for XGBoost

from sklearn.model_selection import KFold
from itertools import product

param_grid = {
        'gamma': [0.01, 0.1, 0.2, 0.3],
        'subsample': [0.8, 0.9, 1.0],
        'colsample_bytree': [0.6, 0.8, 1.0],
        'max_depth': [2, 3, 4],
        'n_estimators': [100, 200]
}

n_cv = 5
kf = KFold(n_splits=n_cv, shuffle=True, random_state=42)
xgb = XGBRegressor(objective="reg:squarederror")
# Perform parameter search manually
list_params = list(product(*param_grid.values()))
mse_cv = np.zeros(shape=(len(list_params),))
j = 1
for train_index, test_index in kf.split(X_train):
  X_tr, X_te = X_train.iloc[train_index], X_train.iloc[test_index]
  y_tr, y_te = y_train.iloc[train_index], y_train.iloc[test_index]
  mse_scores = np.zeros(shape=(len(list_params),))
  for i,params in enumerate(list_params):
    param_dict = dict(zip(param_grid.keys(), params))
    model = XGBRegressor(**param_dict)
    model.fit(X_tr, y_tr)
    y_pred = model.predict(X_te)
    mse = mean_squared_error(y_te, y_pred)
    mse_scores[i] = mse
  mse_cv = mse_cv + mse_scores
  print(f"* Fold: {j} / {n_cv}")
  j += 1
* Fold: 1 / 5
* Fold: 2 / 5
* Fold: 3 / 5
* Fold: 4 / 5
* Fold: 5 / 5
mse_cv /= n_cv
opt_param = dict(zip(param_grid.keys(), list_params[np.argmin(mse_cv)]))
print(opt_param)
model = XGBRegressor(**opt_param)
model = model.fit(X_train.to_numpy(), y_train.to_numpy())
y_pred_xgb_cv = model.predict(X_test.to_numpy())
rmse_xgb_cv = np.sqrt(mean_squared_error(y_test, y_pred_xgb_cv))
df_rmse = pd.concat([df_rmse, pd.DataFrame(
                    {'XGB_CV': [rmse_xgb_cv]})], 
                    axis=1)
df_rmse
{'gamma': 0.01, 'subsample': 1.0, 'colsample_bytree': 1.0, 'max_depth': 4, 'n_estimators': 200}
RF_CV Extra-trees_CV XGB_CV
0 0.007523 0.005515 0.008281

2.3 Stacking: Super Learner

# %pip install gradientcobra
from gradientcobra.superlearner import SuperLearner
from sklearn.preprocessing import StandardScaler
sl = SuperLearner()
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(X_train)
x_test_scaled = scaler.transform(X_test)
sl_fit = sl.fit(X_train, y_train)
sl_fit.draw_learning_curve()
print(f'The selected meta learner is {sl_fit.SuperLearner}')
The selected meta learner is LinearRegression()
y_pred_sl = sl_fit.predict(X_test)
rmse_sl_cv = np.sqrt(mean_squared_error(y_test, y_pred_sl))
df_rmse = pd.concat([df_rmse, pd.DataFrame(
                    {'SLearner_CV': [rmse_sl_cv]})], 
                    axis=1)
df_rmse
RF_CV Extra-trees_CV XGB_CV SLearner_CV
0 0.007523 0.005515 0.008281 0.003753

2.4 Consensual Aggregation: GradientCOBRA

from gradientcobra.gradientcobra import GradientCOBRA

gc = GradientCOBRA(opt_method="grid",
                   bandwidth_list=np.linspace(0.01, 100, 500))
gc_fit = gc.fit(X_train, y_train)
* Grid search progress: 100%|██████████| 500/500 [00:39<00:00, 12.64it/s]
print("Estimated bandwidth :" + str(gc_fit.optimization_outputs['opt_bandwidth'][0]))
Estimated bandwidth :53.71204408817634
import plotly.io as pio
pio.renderers.default = 'notebook'
gc_fit.draw_learning_curve()
y_pred_gc = gc_fit.predict(X_test)
rmse_gc_cv = np.sqrt(mean_squared_error(y_test, y_pred_gc))
df_rmse = pd.concat([df_rmse, pd.DataFrame(
                    {'': [rmse_gc_cv]})], 
                    axis=1)
df_rmse
RF_CV Extra-trees_CV XGB_CV SLearner_CV GradientCOBRA
0 0.007523 0.005515 0.008281 0.003753 0.001945

E. Deep Learning

# This is an example with Keras
from sklearn.metrics import mean_squared_error
from keras.models import Sequential
from keras.layers import Dense, Input, Dropout

from keras.callbacks import Callback

# Input
d = x_train_scaled.shape[1]

model = Sequential()
model.add(Input(shape=(d,)))

# To do
model.add(Dense(16, activation="relu"))
model.add(Dense(8, activation="relu"))
model.add(Dense(1, activation="linear"))

model.compile(optimizer='adam', loss='mean_squared_error', metrics=['mse'])

# I only print every N epochs
class custom_callback(Callback):
    def __init__(self, N):
        super(custom_callback, self).__init__()
        self.N = N

    def on_epoch_end(self, epoch, logs=None):
        if (epoch + 1) % self.N == 0:
            print(f'Epoch {epoch + 1}: loss = {logs["loss"]}, MSE = {logs["mse"]}')
            
print_callback = custom_callback(500)
history = model.fit(x_train_scaled, y_train, epochs=3000, batch_size=256, validation_split=0.1, verbose=0, callbacks=[print_callback])

train_loss = history.history['loss']
val_loss = history.history['val_loss']

import plotly.io as pio
pio.renderers.default = 'notebook'
import plotly.graph_objs as go
# Plot the learning curves
epochs = list(range(1, len(train_loss) + 1))
fig1 = go.Figure(go.Scatter(x=epochs, y=train_loss, name="Training loss"))
fig1.add_trace(go.Scatter(x=epochs, y=val_loss, name="Training loss"))
fig1.update_layout(title="Training and Validation Loss",
                   width=800, height=500,
                   xaxis=dict(title="Epoch", type="log"),
                   yaxis=dict(title="Loss"))
fig1.show()
Epoch 500: loss = 0.00043223437387496233, MSE = 0.00043223437387496233
Epoch 1000: loss = 0.0001070614525815472, MSE = 0.0001070614525815472
Epoch 1500: loss = 6.664307875325903e-05, MSE = 6.664307875325903e-05
Epoch 2000: loss = 5.8001125580631196e-05, MSE = 5.8001125580631196e-05
Epoch 2500: loss = 5.7669451052788645e-05, MSE = 5.7669451052788645e-05
Epoch 3000: loss = 3.066043063881807e-05, MSE = 3.066043063881807e-05
y_pred_dnn = model.predict(x_test_scaled)
rmse_dnn = np.sqrt(mean_squared_error(y_test, y_pred_dnn))
rmse_dnn
40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 2ms/step
0.005447119682704804
y_pred_dnn = model.predict(x_test_scaled)
rmse_dnn = np.sqrt(mean_squared_error(y_test, y_pred_dnn))
df_rmse = pd.concat([df_rmse, pd.DataFrame(
                    {'DNN': [rmse_dnn]})], 
                    axis=1)
df_rmse
40/40 ━━━━━━━━━━━━━━━━━━━━ 0s 6ms/step
RF_CV Extra-trees_CV XGB_CV SLearner_CV GradientCOBRA DNN
0 0.007523 0.005515 0.008281 0.003753 0.001945 0.005447

2. Kaggle Stroke Dataset

Stroke, also known as a cerebrovascular accident (CVA), occurs when blood flow to a part of the brain is interrupted or reduced, depriving brain tissue of oxygen and nutrients. This dataset contains information such as age, gender, hypertension, heart disease, marital status, work type, residence type, average glucose level, and body mass index (BMI). The goal is to use this data to build predictive models that can help identify individuals at high risk of stroke, enabling early intervention and potentially saving lives. It is a very highly imbalanced dataset, you may face challenges in building a model. Random sampling and weighting methods may be considered. For more information, see: Kaggle Stroke Dataset.

path = kagglehub.dataset_download("fedesoriano/stroke-prediction-dataset")

data = pd.read_csv(path + '/healthcare-dataset-stroke-data.csv')
data.head()
Warning: Looks like you're using an outdated `kagglehub` version (installed: 0.3.6), please consider upgrading to the latest version (0.3.7).
id gender age hypertension heart_disease ever_married work_type Residence_type avg_glucose_level bmi smoking_status stroke
0 9046 Male 67.0 0 1 Yes Private Urban 228.69 36.6 formerly smoked 1
1 51676 Female 61.0 0 0 Yes Self-employed Rural 202.21 NaN never smoked 1
2 31112 Male 80.0 0 1 Yes Private Rural 105.92 32.5 never smoked 1
3 60182 Female 49.0 0 0 Yes Private Urban 171.23 34.4 smokes 1
4 1665 Female 79.0 1 0 Yes Self-employed Rural 174.12 24.0 never smoked 1

Reader should try to implement ensemble learning methods to predict this stroke condition of this dataset.

References

\(^{\text{📚}}\) Bagging predictors, Breiman (1996).
\(^{\text{📚}}\) The strength of weak learnability, Robert E. Schapire (1990)..
\(^{\text{📚}}\) COBRA: A combined regression strategy, Beau et al. (2016).
\(^{\text{📚}}\) Gradient COBRA: A kernel-based consensual aggregation for regression, Has (2023).
\(^{\text{📚}}\) Aggregation using input–output trade-off, Fischer & Mougeot (2019).
\(^{\text{📚}}\) Super Learner, M. J. Van der Laan (2007).